Вопрос 4. Частица в потенциальной яме. Квантование энергии

Простейшим примером пространственно-ограниченного движения является одномерное движение квантовой частицы в силовом поле, имеющем вид очень глубокой потенциальной ямы с вертикальными стенками (рис. 6.1).

В этом силовом поле график потенциальной энергии частицы U (x) имеет вид, показанный на (рис 21.1).

Непроницаемость стенок выражается в неограниченном возрастании U(x) в точках х =0 и х=l. Частица может находиться лишь на участке 0< x < l Значение потенциальной энергии частицы в пределах этого участка U(x)= 0. Так как частица не выходит из промежутка 0< x<l, то вероятность ее обнаружения вне этого промежутка равна нулю, что возможно лишь в случае равенства нулю ее волновой функции вне этого участка. Следовательно, уравнение Шрёдингера должно быть дополнено граничными условиями: 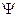(0)=0; 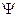(l)=0.

Решение уравнения Шредингера позволяет найти волновую функцию

Рис. 21.1

частицы в области 0< x<l. Пусть силовое поле не меняется с течением времени, поэтому воспользуемся уравнением (21.9) для стационарных состояний, которое в случае U=0 принимает вид:

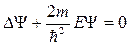. (21.13)

Введем в уравнение волновое число

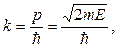(21.14)

тогда уравнение (21.13) для одномерного случая приобретет вид: .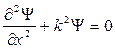

Общим решениемданного однородногодифференциальногоуравнения второго порядка является волновая функция

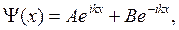(21.15)

где А и B - некоторые комплексные коэффициенты, не зависящие от x. Воспользуемся граничными условиями: Таккак 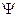(0)=0,то A+B=0 =>B= -A.

Выражению (21.15) придадим следующий вид:

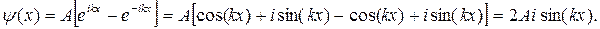
С учетом того, что 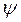(l) = 0, получим sin(kl)=0, откуда 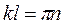, k= 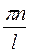, где n =0,1,2,3,... Случай n =0 должен быть отброшен, т.к. в этом случае получается, что 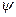(х) =0, т.е. вероятность обнаружения частицы внутри потенциальной ямы равна нулю. Однако с самого начала мы полагали, что частица локализована именно в области 0< x<l. Так как волновое число k принимает дискретный набор значений, то его записывают k _n, а волновую функцию, зависящую от k _{n ,} записывают 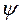_n. Вместо выражения 2 iA удобно ввести новую комплексную постоянную С =2 i A, тогда 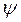_n (х)= C sin (.

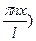Для нахождения амплитуды С волновой функции воспользуемся условием нормировки: .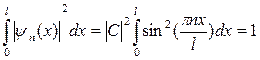

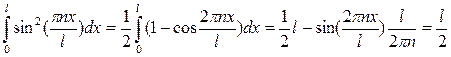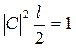Так как , то , С= .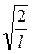

Таким образом,

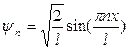. (21.16)

Выразив из (21.14) полную энергию частицы через волновое число получим: E_n = 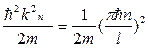, (21.17)

где n = 1, 2, 3….Выражение (21.17) − энергетический спектр частицы в бесконечно глубокой потенциальной яме. Этот энергетический спектр дискретен. Главное квантовое число n задает уровни энергии.

Из выражения (21.17) следует, что энергетический интервал между двумя соседними уровнями энергии равен:

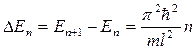. (21.18)

Например, для электрона при размерах ямы l =10^-1 м (свободные электроны в металле) Δ En ≈ 10^-35 n Дж ≈10^-16 n эВ, т.е. энергетические уровни расположены столь тесно, что спектр можно считать практически непрерывным. Если же размеры ямы соизмеримы с размерами стенки (l ≈

10 ^-10 м), то для электрона Δ En ≈ 10^-17 n Дж ≈10^-2 n эВ, т.е. получаются явно дискретные значения энергии (линейчатый спектр). Таким образом, применение уравнения Шредингерак частице в потенциальной яме с бесконечно высокими стенками приводит к квантовым значениям энергии и координат, в то время как классическая механика наэнергию этой частицы лишних ограничений не накладывает. Кроме того, квантово-механическое рассмотрение этой задачи приводит к выводу, что частица в потенциальной яме с бесконечно высокими стенками не может иметь энергию меньшую, чем минимальная энергия, равная E₁ = .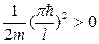

Наличие отличной от нуля минимальной энергии не случайно и вытекает из соотношения неопределенностей. Неопределенность координаты Δ x частицы в яме шириной l равна: Δ x = l. Тогда согласно соотношению неопределенностей, импульс не может иметь точное, в данном случае нулевое, значение. Неопределенность импульса: .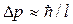

Такому разбросу значений импульса соответствует кинетическая энергия

.

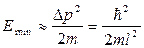Все остальные уровни имеют энергию, превышающую это значение.

Из функций (21.17) и (21.18) следует, что при больших квантовых числах (n >>1) 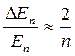<< 1, т.е. соседние уровни расположены близко друг к другу, причем, с увеличением n уровни сближаются. Если п очень велико, то можно говорить о непрерывной последовательности уровней, и характерная особенность квантовых процессов – дискретност ь – становится неразличимой.

Этот результат является частным случаем принципа соответствия Бора, согласно которому законы квантовой механики должны прибольших значениях квантовых чисел переходить в законы классическойфизики.

Более общая трактовка принципа соответствия: всякая новая, более общая теория, являющаяся развитием классической, не отвергает ее полностью, а включает в себя классическую теорию, указывая границы ее применимости, причем в определенных предельных условиях новая теория переходит в старую.

При главном квантовом числе n =1 энергия частицы минимальна и принимает значение:

E₁= 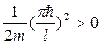. (21.19)

Отсюда следует, что микрочастица не может обладать энергией, равной нулю

(т.е. частица не может находиться на дне потенциальной ямы), что означает невозможность остановки микрочастицы в классическом смысле.

Таким образом, микрочастицав «потенциальной яме» с бесконечно высокими стенками может находиться только на определенном энергетическом уровне E n, или, как говорят, частица находится в квантовом состоянии п.

На рис. 21.2 а показано расположение энергетических уровней

Рис. 21.2

частицы; графики собственных функций изображены на рис.21.2 б; на рис.21.2 в дана плотность вероятности обнаружения частицы на различных расстояниях от стенок ямы.

Анализ формулы (21.17) показывает, что при больших значениях главного квантового числа n дискретность энергетических уравнений становится неразличимой и не влияет на движения электрона, т.е. происходит переход к классическому случаю. Аналогичное влияние оказывает увеличение массы микрообъекта и размеров потенциальной ямы.

Дата добавления: 2014-11-06