Вопрос 5. Прохождение частицы сквозь потенциальный барьер

Способность квантовых частиц в силу своих волновых свойств заходить за барьер приводит к так называемому туннельному эффекту. Он заключается в следующем. Если частица с энергией Е налетает на некоторый потенциальный барьер 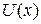, то она с определенной вероятностью может пройти сквозь барьер как бы по туннелю при E < U.

Рассмотрим простейший потенциальный барьер прямоугольной формы

(рис. 21.3) высоты U и ширины l для одномерного (по оси OX) движения частицы.

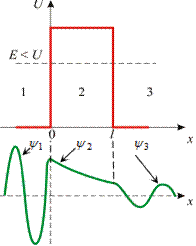
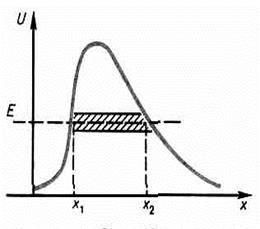
Рис. 21.3 Рис. 21.4

Для такого барьера

U (x) = 0, (x < 0; обл. 1);

U (x) = U, (0 < x < l; обл. 2);

U (x) = 0, (x > l;обл. 3).

При данных условиях задачи классическая частица, обладая энергией Е, либо беспрепятственно пройдет над барьером при E > U, либо отразится от него при E < U и будет двигаться в обратную сторону, т.е. она не может проникнуть через барьер.

Для микрочастиц же, даже при E < U, имеется отличная от нуля вероятность, что частица отразится от барьера и будет двигаться в обратную сторону и также имеется отличная от нуля вероятность, что частица окажется в области x > l, т.е. проникнет сквозь барьер. Такой вывод следует непосредственно из решения уравнения Шредингера, описывающего движение микрочастицы при данных условиях задачи.

Решением уравнения Шредингера для каждой из выделенных областей являются волновые функции 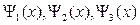, показанные на рис. 21.3 (нижняя часть рисунка). Из рисунка следует, что волновая функция не равна нулю и внутри барьера, а вобласти3, если барьер не очень широк, опять имеет вид волнде Бройля с тем же импульсом, т.е. с той же частотой, но с меньшей амплитудой.

Таким образом, квантовая механика приводит к принципиально новому квантовому явлению – туннельному эффекту, в результатекоторого микрообъект может пройти через барьер.

Коэффициент прозрачности, т.е. вероятность прохождения частицы сквозь барьер прямоугольной формы, определяется выражением

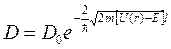, (21.19а)

где m –масса частицы; E – ее энергия; l – ширина барьера; U – его высота.

Коэффициент прозрачности барьера произвольной формы (рис. 21.4) имеет вид:

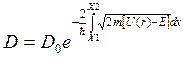. (21.19б)

Прохождение частицы сквозь барьер можно пояснить соотношением неопределенностей. Неопределенность импульса на отрезкеΔ x = l составляет Δ p > 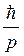.Связанная с этим разбросом кинетическая энергия 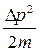может оказаться достаточной для того, чтобы полная энергия оказалась больше потенциальной и частица может пройти сквозь барьер.

Туннельный эффект – специфически квантовое явление, не имеющее аналога в классической физике. Туннельное прохождение сквозь потенциальный барьер лежит в основе многих явлений физики твердого тела (например, явления в контактном слое на границе двух полупроводников, холодная эмиссия электронов из металла), атомной и ядерной физики (например, α - распад, протекание термоядерных реакций) и др. На использовании явления туннельного эффекта создан сканирующий туннельный микроскоп, позволяющий определять профили поверхности тончайших пленок. Разрешающая способность микроскопа по осям x, y достигает 10^-10 м, а по оси z − порядка 10^-12 м.

Дата добавления: 2014-11-06