П1] [п2] . Коэффициент корреляции Пирсона. Коэффициент детерминации. Прямая линия регрессии

Часто на практике каждый объект в выборке изучается по двум признакам Х и У с целью исследования зависимости между ними.

Пример: Пусть Х – познавательная активность по предмету, У– успеваемость по этому же предмету учеников в классе.

Допустим, сделана выборка объема n =5:

((3,3), (2,4), (1,5), (1,4), (4,3)).

Здесь первое число в каждой паре – познавательная активность по предмету, а второе число в каждой паре есть успеваемость по этому предмету (в баллах). Каждая пара соответствует одному ученику.

С целью графического изображения выборки по двум признакам Х и У строят корреляционное поле: в системе координат ХОУ отмечают точки с координатами (х_i, у_i). Для нашего примера корреляционное поле выглядит следующим образом:

	Успеваемость у

5
4
Познавательная активность 1

х

Для изучения зависимости между Х _и У вычисляют выборочный коэффициент корреляции Пирсона r_в :

r_в=  

ХУ_в – Х _в У_в

s_в (Х) s_в(У)

Здесь ХУ_в – выборочная средняя произведения

ХУ_в = (х₁у₁ + х₂у₂ + … + х_nу_n),

Х_в,У_в – выборочные средние признаков Х,У;

s_в (Х), s_в(У) – выборочные средние квадратические отклонения.

Всегда –1< r_в <1. Если | r |>0,3, то зависимость сильная, если | r |<0,3, то зависимость слабая. Если r>0, то зависимость положительная: чем больше Х, тем больше У. Если r<0, то зависимость отрицательная: чем больше Х, тем меньше У.

Найдем выборочный коэффициент корреляции для нашего примера. Вычисления оформим в виде таблицы:

№	Х	У	Х^2	У^2	ХУ
å

Отсюда

Х_в ==2,2; У_в = =3,8; Х_в² = = 6,2;

У_в² = =15; ХУ_в = =7,6

Д_в(У)=15 – 3,8² = 0,56; Д_{в испр.}(У)= 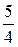0,56= 0,7; s_{в испр.} (У)» 0,84;

Д_в (Х) = 6,2 – 2,2² = 1,36; Д_{в испр.} (Х) = 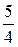1,36 = 1,7; s_{в испр.} (Х)»1,30;

r_в = » - 0,8.

Вывод: Зависимость между познавательной активностью и успеваемостью сильная отрицательная: чем выше познавательная активность, тем выше успеваемость.

Определение 6. Коэффициентом детерминации называется квадрат коэффициента корреляции

d _в = r_в² .

В нашем примере

d _в = 0,64.

Коэффициент детерминации, выраженный в процентах, показывает, какая доля изменчивости переменной У обусловлена изменчивостью переменной X.

В корреляционном поле можно построить прямую линию, к которой точки корреляционного поля «наиболее близки». Эта прямая линия называется прямой линией регрессии. Ее уравнение имеет следующий вид:

.

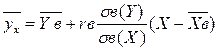Здесь у_х – среднее значение у при данном х (у_х – аналог переменной у в уравнении прямой у=кх+ в).

В нашем примере уравнение регрессии принимает вид

у_х = 3,8 + (- 0,8) 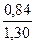(х – 2,2),

у_х = - 0,45х + 4,79.

Построим данную прямую в корреляционном поле по точкам

x
у	4,79	2,54

5
4
3

По уравнению прямой регрессии можно вычислить среднее значение у_х для данного х. Найдем у_х при х = 1; при х = 3. Для этого подставим х = 1, затем х = 3 в уравнение регрессии; получаем:

–

у_{х = 1} = 4,34 (б.) – средняя успеваемость учеников при постоянном увлечении предметом; у_{х = 3} = 3,44 (б.) – средняя успеваемость учеников с периодическим интересом к предмету.

Ранговая корреляция Спирмена.

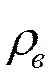= 1- (*)

Использование коэффициента корреляции Пирсона для изучения зависимости между X и Y предполагает выполнение некоторых условий

на выборку, одно из которых – нормальность совместного распределения переменных X и Y.Поэтому в некоторых случаях

целесообразно использовать ранговую корреляцию Спирмена или Кендалла.

В ранговых корреляциях исследуется зависимость не между значениями переменных X и Y, а между рангами этих значений. К оэффициент ранговой корреляции Спирмена вычисляется по формуле

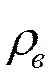= 1- ,

Здесь n – объем выборки, а d_i - разность соответствующих рангов. Для вычислений рангов, разностей рангов и суммы квадратов разностей рангов удобно составлять расчетную таблицу.

Пример. Вычислим коэффициент ранговой корреляции Спирмена для предыдущего примера. Составим расчетную таблицу.

N	xi	yi	ai	bi	di	di^2

В столбцах x_i, y_i записаны значения из выборки. В столбцах a_i, b_i мы запишем ранги переменных x_i, y_i соответственно. Сначала занумеруем значения x_i, y_i в порядке ухудшения качества: к каждому значению припишем его номер (в той же клетке таблицы).

N	xi	yi	ai	bi	di	di^2
	1 1	5 1
	1 2	4 2
	2 3	4 3
	3 4	3 4
	4 5	3 5

В столбцах a_i, b_i мы запишем ранги: ранг значения равен его номеру, если значение встречается в выборке только один раз и ранг равен среднему арифметическому номеров всех одинаковых значений, если значение встречается несколько раз.

N	xi	yi	ai	bi	di	di^2
	1 1	5 1	1,5
	1 2	4 2	1,5	2,5
	2 3	4 3		2,5
	3 4	3 4		4,5
	4 5	3 5		4,5

Проверка правильности вычисления рангов: сумма рангов по каждой переменной должна быть равна n(n+1)/2. В нашем примере это число равно 5(5+1)/2=15.Ранги вычислены верно.

В столбце d_i записываем разности рангов

d_i= a_i - b_i.

N	xi	yi	ai	bi	di	di^2
	1 1	5 1	1,5		0,5
	1 2	4 2	1,5	2,5	- 1
	2 3	4 3		2,5	0,5
	3 4	3 4		4,5	- 0,5
	4 5	3 5		4,5	0,5

В столбце d_i² записываем квадраты разностей рангов.

N	xi	yi	ai	bi	di	di^2
	1 1	5 1	1,5		0,5	0,25
	1 2	4 2	1,5	2,5	- 1
	2 3	4 3		2,5	0,5	0,25
	3 4	3 4		4,5	- 0,5	0,25
	4 5	3 5		4,5	0,5	0,25

Находим сумму чисел последнего столбика

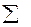d_i² =2.

1 Подставляем полученные данные в формулу (*)

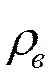=1 - =1- =0,7.

Выводы по коэффициенту ранговой корреляции 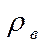аналогичны выводам по коэффициенту корреляции Пирсона r_в. Всегда

Если коэффициент ранговой корреляции больше нуля, то связь прямая: чем лучше качество по X, тем лучше качество по Y; Если коэффициент ранговой корреляции меньше нуля, то связь обратная: чем лучше качество по X, тем хуже качество по Y. В нашем примере коэффициент ранговой корреляции Спирмена больше нуля, связь прямая: чем выше познавательная активность учащихся, тем выше их успеваемость. Полный вывод: повышение познавательной активности учащихся существенно повышает их успеваемость.

Пример. Проверить согласованность оценок поведения детей родителями (X) и педагогом (Y).Поведение детей оценивалось по десятибалльной шкале (меньше –лучше).

Выполнена выборка объема n=10.

X
Y

Для исследования согласованности оценок мы

вычислим коэффициент ранговой корреляции Спирмена. Составляем расчетную таблицу:

N	xi	yi	ai	bi	di	di^2
	2 1	3 1		1.5	- 0.5	0.25
	3 2	4 3			- 1
	4 3	3 2	3.5	1.5
	4 4	5 4	3.5	4,5	- 1
	5 5	7 6		6.5	- 1.5	2.25
	6 6	5 5		4,5	1,5	2,25
	7 7	7 7		6.5	0.5	0.25
	8 8	9 8	8.5	8.5
	8 9	9 9	8.5	8.5
	9 10	10 10

Выполним

проверку правильности составления

рангов: сумма рангов по каждой переменной должна быть равна 10(10+1)/2=55. Ранги вычислены верно.

Находим сумму чисел последнего столбика

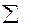d_i² =11.

Подставляем полученные данные в формулу (*): =1 - =1- =0,93 .

Вывод: Так как коэффициент ранговой корреляции Спирмена 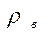близок к единице, то

оценки поведения детей родителями и педагогом очень хорошо согласованы.

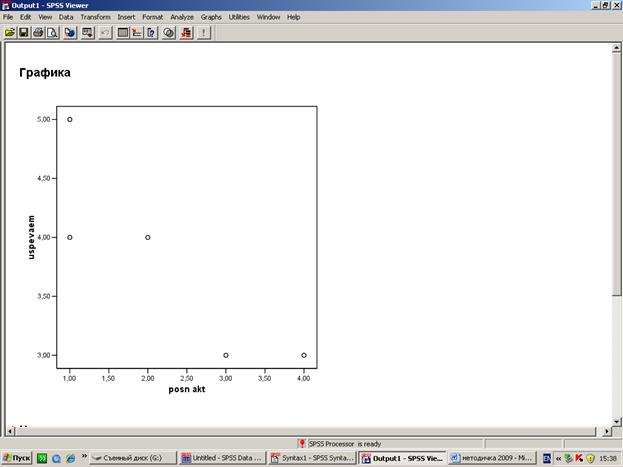
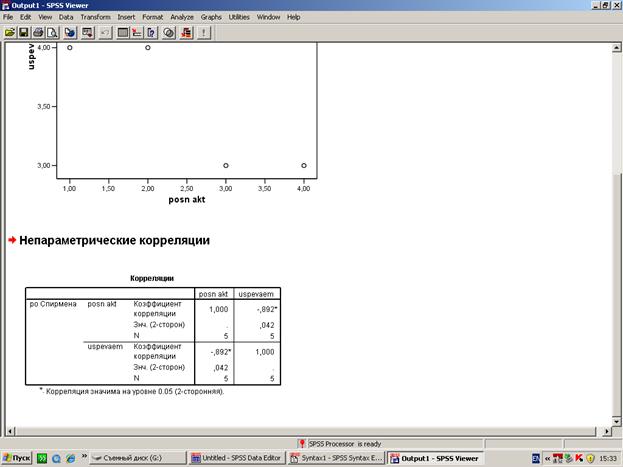
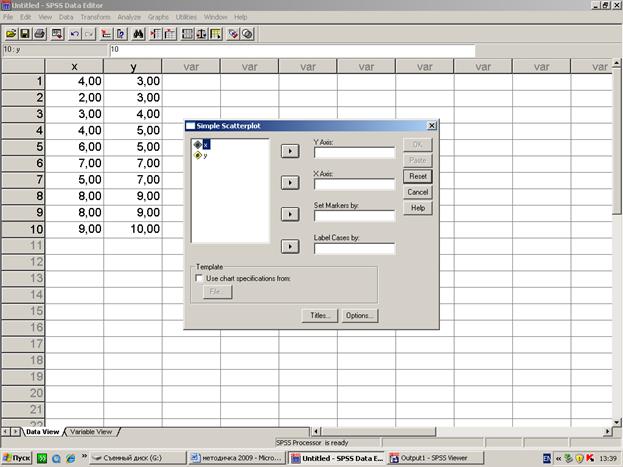
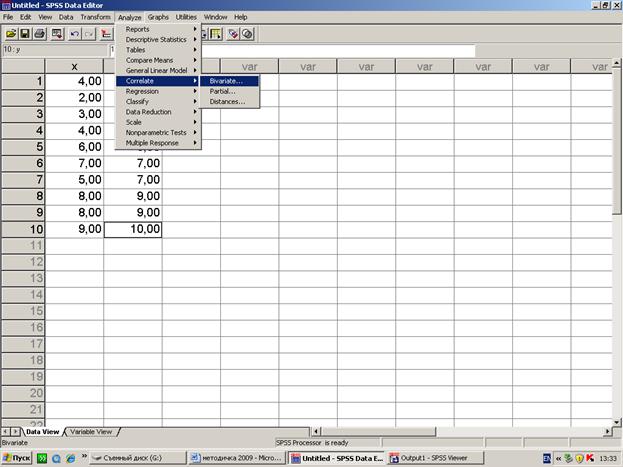
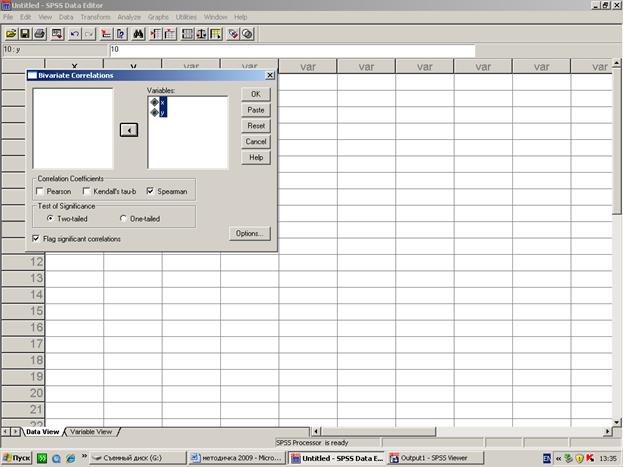
Обработка данного примера в среде SPSS:

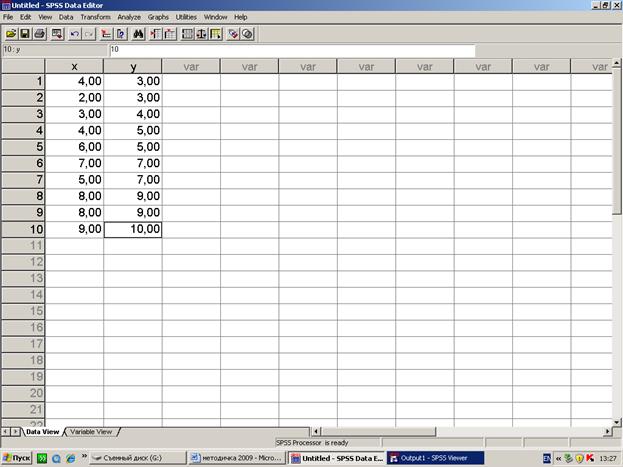[п3]

Дата добавления: 2014-11-06