Согласованная фильтрация детерминированного сигнала

Синтез оптимального фильтра – это отыскание передаточной характеристики устройства, обеспечивающего оптимизацию сигнал/шум на выходе 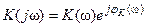, т. е. задача сводится к отысканию АЧХ и ФЧХ устройства.

Естественно, результаты синтеза будут ограничены входными данными.

Пусть сигнал s (t) действует на фоне шума с постоянным энергетическим спектром (белый шум). Введем в рассмотрение время t ₀ – это время, за которое производится фиксация уровня сигнал/шум. Выходной сигнал представим в виде

.

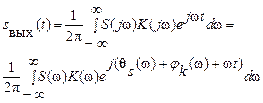Среднеквадратическое значение помехи на выходе фильтра

,

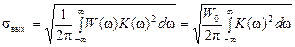где W (w) – энергетический спектр помехи.

Отсюда следует:

.

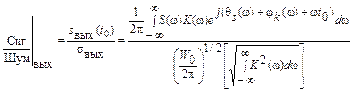Необходимо, чтобы это соотношение было максимальным. Для этого воспользуемся неравенством Буняковского-Шварца:

.

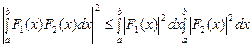Это неравенство обращается в равенство только при выполнении условия 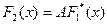, где А – произвольный постоянный коэффициент.

В нашем случае

, .

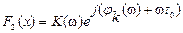Отсюда

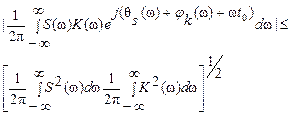
Таким образом,

.

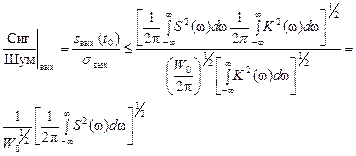Учитывая, что выражение в квадратных скобках есть полная энергия входного сигнала Э, запишем окончательное выражение: .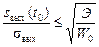

Это неравенство обращается в равенство при выполнении условия

.

Откуда

.

Фильтр с таким коэффициентом передачи называется фильтром, согласованным с сигналом. Он обеспечивает на выходе максимально возможное соотношение:

.

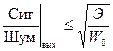АЧХ: , ФЧХ: .

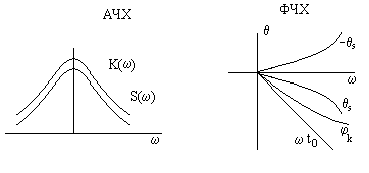
Коэффициент А – размерный коэффициент, который приводит к безразмерному коэффициенту передачи. Добавление w t ₀ делается для выделения всей энергии сигнала.

ВЫВОД. Фильтр обеспечивает максимально возможное соотношение сигнал/шум на выходе за счет:

1. Условия компенсации начальных фаз гармонических составляющих сигнала, так как ФЧХ фильтра равна и противоположна по знаку ФЧХ сигнала.

2. За счет совпадения формы K (w) и S (w) фильтр пропускает составляющую шума неравномерно, что приводит к уменьшению шума на выходе.

3. Сигнал ослабляется слабее, чем шум. Это приводит к максимуму отношения сигнал/шум на выходе.

Дата добавления: 2014-11-06