Определение изобарной молярной теплоемкости природных газов

Удельная теплоемкость — количество теплоты, со­общаемой единице массы вещества, чтобы изменить его тем­пературу на один градус. Для газов различают изобарную с_р и изохорную с_v удельные теплоемкости,

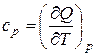
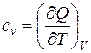Ошибка! Ошибка связи. (Ш.59)

где индексы у скобок означают давление р = const и объем V= const.

Согласно первому началу термодинамики имеем dQ=dt—Vdp, (III. 60)

где Q — количество теплоты; V — объем системы; i— энтальпия (теплосодержание). di = c_pdT + . (III.61)

При изобарном процессе (р = const) изменение количества теплоты системы равно изменению ее энтальпии dQ = di = C_pиdT (II1.62)

или 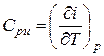(Ш-63)

Изобарная молярная теплоемкость идеальных газов Сри за­висит от температуры. Зависимость молярной теплоемкости компонентов природных газов при атмосферном давлении от температуры приближенно можно выразить формулой

С_ри = 0,523 (8,36+0,00892t) 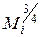, кДж/(кмоль-К), (III.64)

где Mi — молекулярная масса углеводорода, являющегося ком­понентом природного газа (от метана до гептана включительно)

Погрешность расчетов по формуле (III. 64) для углеводоро­дов CH₄-C₅H₁₂ в интервале температур минус 40 °С плюс 120 ^ОС не превышает 5%, для углеводородов С₆Н₁₄—С₇Н₁₆ в том же интервале температур не превышает 10 %.

Изобарная молярная теплоемкость неуглеводородных ком­понентов природных газов (азота, углекислого газа, сероводо­рода) равна примерно половине теплоемкости углеводорода с одинаковой молекулярной массой при одинаковой темпера­туре.

Например, изобарная молярная теплоемкость CO₂(C_ри=44) равна половине молярной теплоемкости пропана С₃Н₈ (С_ри=44), которая рассчитывается по формуле (111.64).

Теплоемкость смесей газов определяется по правилу адди­тивности(II1.65)

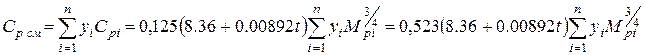
где y_i - молярная доля i -ro компонента в смеси; c_pi — изобар­ная молярная теплоемкость i-ro компонента.

Изобарная молярная теплоемкость реальных природных га­зов зависит от давления и температуры С_р = С_ри(t) + DС_р(р, t), (Ш.66)

где DС_р(р, t) —изотермическая поправка теплоемкости на дав­ление (рис. III.9).

Изобарную молярную теплоемкость природного газа можно рассчитать и по формуле, предложенной Л. М. Гухманом и Т. В. Нагаревой:

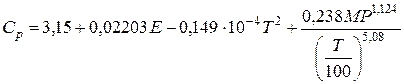(III.67)

При решении задач, связанных с добычей, транспортом, хранением и переработкой природных газов, наиболее употре­бительны двухконстантные уравнения состояния и восьмиконстантные.

Рис. III.9. Зависимость изотермической поправки изобарной мольной теплоемкости DС_р(р, t) от приведенных абсолютных давления р_пр и температуры Т_пр

Последней, наиболее удачной модификацией двухконстантного уравнения состояния природных газов, предложенной в 1975 г., является уравнение состояния Пенга — Робинсона

(III.68)

где V —молярный объем; а(Т), b — коэффициенты уравнения, определяемые критическими параметрами вещества (коэффи­циент а(Т) —фракция температуры).

Уравнение состояния Пенга—Робинсона, записанное отно­сительно коэффициента сверхсжимаемости z, имеет вид z³-(1-В)z²+(А-3В²-2В)z-(АВ—В²-B³)=0, (69)

где ; 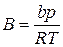(III.70)

Уравнение (III.69) имеет один или три действительных корня. Если смесь находится в двухфазном состоянии, то больший корень относится к паровой фазе, а наименьший положитель­ный корень — к жидкой фазе.

При критических условиях (z_кp = 0,307)

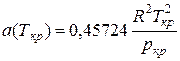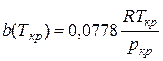; (Ш.71)

При температурах, отличных от критической,

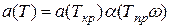; , (111.72)

где 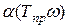— безразмерная функция приведенной темпера­туры Т_пр и ацентрического фактора w; при критической темпе­ратуре a=1.

Для всех веществ зависимость между a^0,5 и Т^0,5_пр может быть аппроксимирована уравнением прямой a^0,5 =1+m(1- Т^0,5_пр), (III.73)

где коэффициент m, определяющий угол наклона прямой к оси Т^0,5_пр, является функцией ацентрического фактора w: m=0,37464+1,5422bw—0,26992w². (III.74)

При использовании уравнения Пенга—Робинсона для расчета термодинамических и физических свойств многокомпонентных смесей коэффициенты а_cм(Т) и b_см вычисляют по следующим формулам:

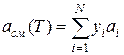
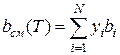(111.75)

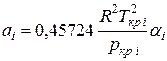
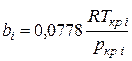(III.76).

Отклонение теплофизических свойств реальных природных га­зов от идеальных можно определить с использованием уравне­ния состояния Пенга — Робинсона.

Отклонение энтальпии реального газа

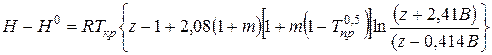(III.77)

где Н° — энтальпия идеального газа.

Энтальпийная диаграмма природного газа изображена на рис. III.10.

Рис. III.10. Энтальпийная диаграмма природного газа

Отклонение молярной изобарной теплоемкости реального газа

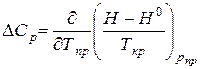. (III_78)

Зависимость DС_р от р_пр и Т_пр изображена на рис. III.9

Разность изобарной и изохронной молярных теплоемкостей реального газа

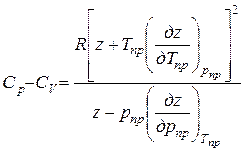(79)

где (80)

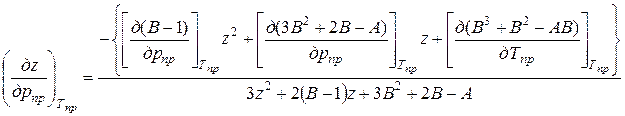(81)

Дата добавления: 2014-11-07