
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Сделать чертеж
|
|
|
|
Уравнение плоскости АВС;
Уравнение прямой АВ;
Угол между ребрами АВ и АD;
Длину ребра АВ;
Исследовать функции методом дифференциального исчисления и схематично построить их графики.
Вычислить пределы функций, не пользуясь правилом Лопиталя.
Найти матрицу, обратную данной. Выполнить проверку.
| Вариант | Матрица 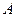
| Вариант | Матрица 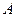
|
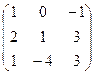
| 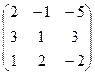
| ||
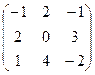
| 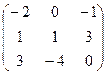
| ||

| 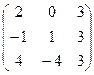
| ||
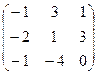
| 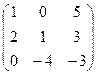
| ||
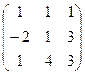
| 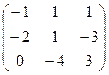
|
31-40. Даны координаты вершин пирамиды А, В, С, D. Требуется найти: 1) длину ребра АВ; 2) угол между ребрами АВ и АС; 3) уравнение прямой АВ; 4) уравнение плоскости АВС. Сделать чертеж.
11. А(2, 0, 2), В(3, 1, 2), С(4,2,0), D(1,1,1).
12. А(3, 1, 2), В(4, 0, 3), С(2,1,-1), D(0,-3,2).
13. А(3, 1, 2), В(0, 0, 6), С(3,2,1), D(0,4,1).
14. А(2, 0, 3), В(-1, 4, 2), С(3,2,1), D(1,2,3).
15. А(2, 0,-3), В(-3, 4, 2), С(5,7,0), D(4,2,1).
16. А(-1, 1, 3), В(1, 0, 0), С(5,-2,1), D(-1,-1,0).
17. А(2, 7,-5), В(2, 0,-1), С(-2,-4,6), D(3,2,-1).
18. А(3, 8, 5), В(2, 3, 5), С(-3,-5,1), D(0,2,1).
19. А(2, 3, 6), В(-3, 0, 1), С(6,-3,1), D(4,3,-1).
20. А(3,-1, 2), В(0,-3, 1), С(0,0,2), D(4,7,-1).
41-50. Доказать совместность данной системы линейных уравнений и решить ее тремя способами: 1) методом Крамера; 2) методом Гаусса; 3) средствами матричного исчисления.
41. 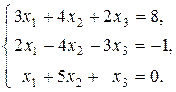 42.
42. 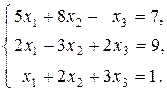
43. 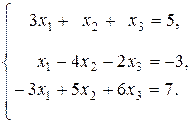 44.
44. 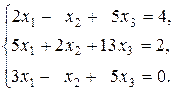
45. 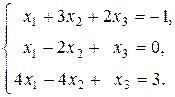 46.
46. 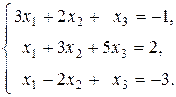
47. 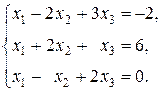 48.
48. 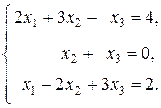
49. 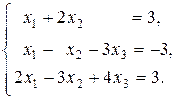 50.
50. 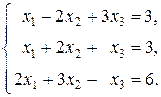
51. а) 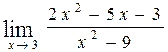 , б)
, б) 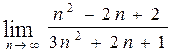 ,
,
в)  , г)
, г) 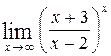 .
.
52. а) 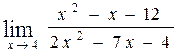 , б)
, б) 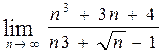 ,
,
в) 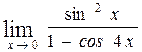 , г)
, г) 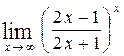 .
.
53. а) 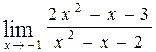 , б)
, б) 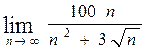 ,
,
в) 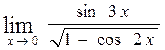 , г)
, г) 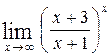 .
.
54. а) 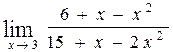 , б)
, б) 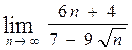 ,
,
в) 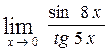 , г)
, г) 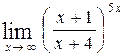 .
.
55. а) 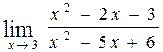 , б)
, б) 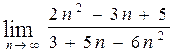 ,
,
в) 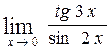 , г)
, г) 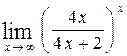 .
.
56. а) 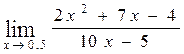 , б)
, б) 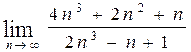 ,
,
в) 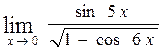 , г)
, г) 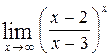 .
.
57. а)  , б)
, б) 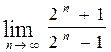 ,
,
в) 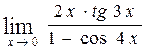 , г)
, г) 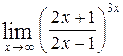 .
.
58. а) 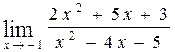 , б)
, б) 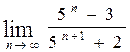 ,
,
в) 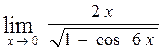 , г)
, г) 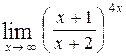 .
.
59. а) 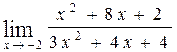 , б)
, б) 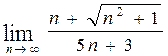 ,
,
в) 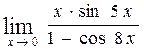 , г)
, г) 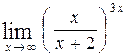 .
.
60. а)  , б)
, б) 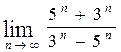 ,
,
в) 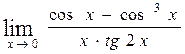 , г)
, г) 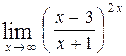 .
.
61-70. Найти производные данных функций.
61. а)  ; б)
; б) 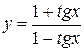 ;
;
в) 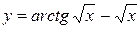 ;
;
62. а) 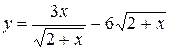 ; б)
; б) 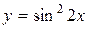 ;
;
в) 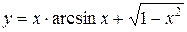 ;
;
63. а) 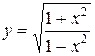 ; б)
; б) 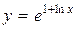 ;
;
в) 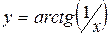 ;
;
64. а) 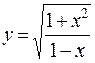 ; б)
; б) 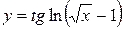 ;
;
в) 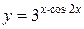 ;
;
65. а) 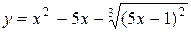 ; б)
; б) 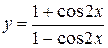 ;
;
в) 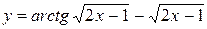 ;
;
66. а) 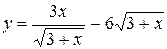 ; б)
; б) 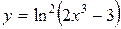 ;
;
в) 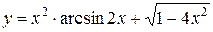 ;
;
67. а) 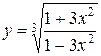 ; б)
; б) 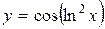 ;
;
в) 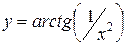
68. а) 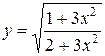 ; б)
; б) 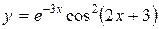 ;
;
в) 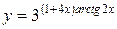 ;
;
69. а)  ; б)
; б) 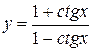 ;
;
в) 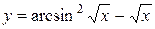 ;
;
70. а) 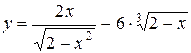 ; б)
; б)  ;
;
в) 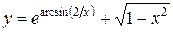 ;
;
71. а) 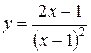 ;
;
72. а) 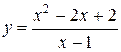 ;
;
73. а) 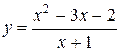 ;
;
74. а) 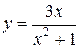 ;
;
75. а) 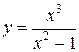 ;
;
76. а) 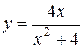 ;
;
77. 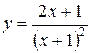
78. 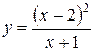
79. 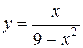
80. 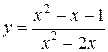
Решение типового варианта
Пример 1. Вычислить определители:
а) 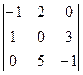 ; б)
; б) 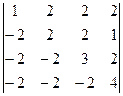 .
.
Решение:
Определитель равен сумме произведений элементов какой−либо строки или столбца на их алгебраические дополнения: 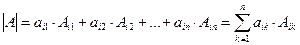 . Алгебраическим дополнением
. Алгебраическим дополнением 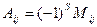 некоторого элемента определителя называется минор этого элемента, умноженный на (−1)S, где
некоторого элемента определителя называется минор этого элемента, умноженный на (−1)S, где 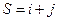 – сумма номеров строки и столбца, на пересечении которых стоит данный элемент. Минором некоторого элемента определителя называется определитель, полученный из исходного вычеркиванием строки и столбца, на пересечении которых стоит данный элемент.
– сумма номеров строки и столбца, на пересечении которых стоит данный элемент. Минором некоторого элемента определителя называется определитель, полученный из исходного вычеркиванием строки и столбца, на пересечении которых стоит данный элемент.
Выберем в рассматриваемом определителе любую строку. Например, первую строку. Тогда определитель может быть вычислен по формуле
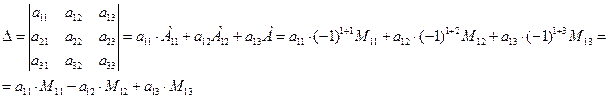

 где
где 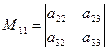 − минор элемента
− минор элемента 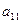 , полученный вычеркиванием из исходного определителя первой строки и первого столбца, на пересечении которых находится элемент
, полученный вычеркиванием из исходного определителя первой строки и первого столбца, на пересечении которых находится элемент 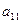 :
: 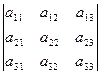 ,
,


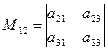 − минор элемента
− минор элемента 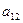 , полученный вычеркиванием из исходного определителя первой строки и второго столбца, на пересечении которых находится элемент
, полученный вычеркиванием из исходного определителя первой строки и второго столбца, на пересечении которых находится элемент 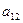 :
: 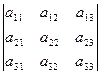 ,
,


 − минор элемента
− минор элемента 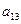 , полученный вычеркиванием из исходного определителя первой строки и третьего столбца, на пересечении которых находится элемент
, полученный вычеркиванием из исходного определителя первой строки и третьего столбца, на пересечении которых находится элемент 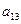 :
: 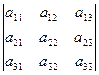 .
.
Выполним задание для первого определителя:
М22 = 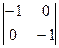 = (−1) × (−1) – 0 × 0 = 1 – 0 = 1,
= (−1) × (−1) – 0 × 0 = 1 – 0 = 1,
А23 = (−1)2+3 × М23 = (−1) × ((−1)×5 − 2×0) = 5.
Вычислим определитель, разложив его по элементам первой строки: 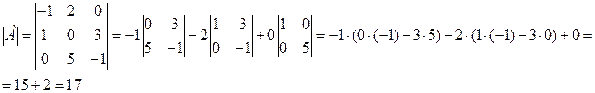 .
.
б) Выполним задание для второго определителя, раскрывая все определители по элементам первой строки:
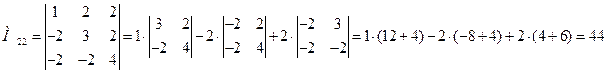
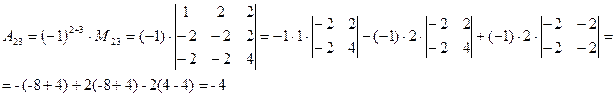
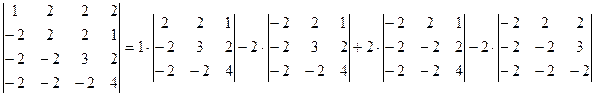 .
.
Полученные определители третьего порядка сведем к определителям второго порядка, еще раз разложив каждый из них по первой строке.
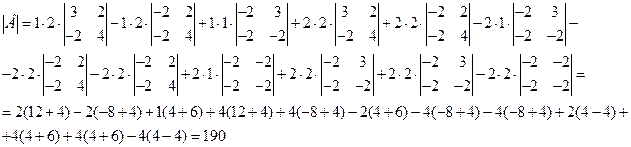 Ответ: а)
Ответ: а) 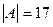 ,
, 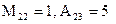 ; б)
; б) 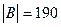 ,
, 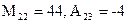 .
.
Пример 2. Даны матрицы 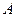 и
и 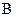 . Вычислить
. Вычислить 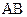 и
и 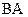 , если они существуют.:
, если они существуют.:
а) 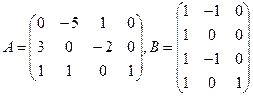 ;
;
Решение:
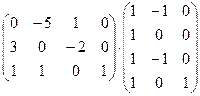
определим размер матрицы, которую получим в результате умножения: первая матрица имеет размер 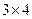 , вторая −
, вторая − 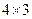 . Берем количество строк у первой матрицы, а количество столбцов – у второй. Таким образом, получаем размер
. Берем количество строк у первой матрицы, а количество столбцов – у второй. Таким образом, получаем размер 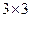 .
.
Для того, чтобы найти элемент 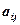 необходимо
необходимо 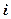 − ю строку первой матрицы умножить скалярно на
− ю строку первой матрицы умножить скалярно на 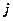 −й столбец второй матрицы
−й столбец второй матрицы
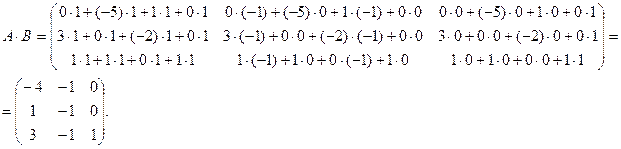
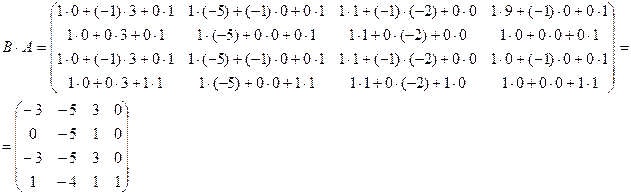 Ответ:
Ответ: 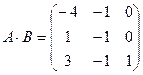 ;
; 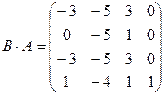 .
.
Пример 3. Определить, имеет ли данная матрица обратную, найти обратную матрицу к данной 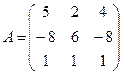 .
.
Решение:
Обратную матрицу к данной матрице 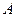 будем находить по следующему плану:
будем находить по следующему плану:
1. Вычислим определитель матрицы 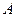
2. Вычислим алгебраические дополнения для всех элементов матрицы 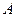 по формуле
по формуле
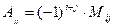 ,где
,где  минор элемента
минор элемента 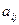 матрицы
матрицы  .
.
3. Запишем матрицу 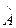 , элементами которой являются соответствующие алгебраические дополнения
, элементами которой являются соответствующие алгебраические дополнения
4. Найдем транспонированную матрицу 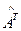
5. Найдем обратную матрицу по формуле 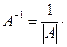
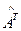
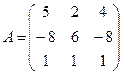
1. Вычислим определитель матрицы  по формуле
по формуле

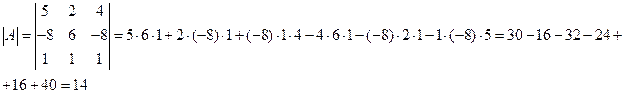
2. Вычислим алгебраические дополнения для всех элементов матрицы 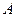
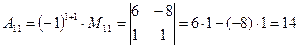
(для вычисления минора 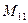 вычеркиваем в матрице
вычеркиваем в матрице 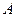 первую строку и первый столбец)
первую строку и первый столбец)
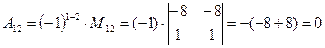
(для вычисления минора 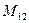 вычеркиваем в матрице
вычеркиваем в матрице 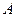 первую строку и второй столбец)
первую строку и второй столбец)
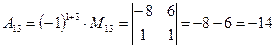
(для вычисления минора 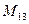 вычеркиваем в матрице
вычеркиваем в матрице 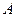 первую строку и третий столбец)
первую строку и третий столбец)
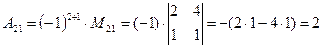
(для вычисления минора 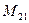 вычеркиваем в матрице
вычеркиваем в матрице 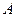 вторую строку и первый столбец)
вторую строку и первый столбец)
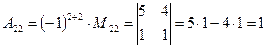
(для вычисления минора 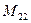 вычеркиваем в матрице
вычеркиваем в матрице 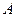 вторую строку и второй столбец)
вторую строку и второй столбец)
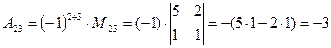
(для вычисления минора 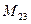 вычеркиваем в матрице
вычеркиваем в матрице 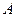 вторую строку и третий столбец)
вторую строку и третий столбец)
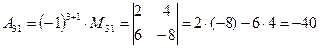
(для вычисления минора 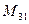 вычеркиваем в матрице
вычеркиваем в матрице 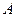 третью строку и первый столбец)
третью строку и первый столбец)
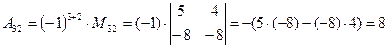
(для вычисления минора 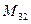 вычеркиваем в матрице
вычеркиваем в матрице 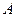 третью строку и второй столбец)
третью строку и второй столбец)
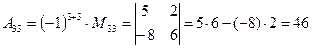
(для вычисления минора 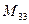 вычеркиваем в матрице
вычеркиваем в матрице 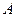 третью строку и третий столбец)
третью строку и третий столбец)
3. Запишем матрицу 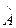 , элементами которой являются найденные алгебраические дополнения
, элементами которой являются найденные алгебраические дополнения

4. Найдем транспонированную матрицу 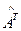 (строки становятся столбцами, а столбцы – строками с сохранением порядка)
(строки становятся столбцами, а столбцы – строками с сохранением порядка)
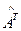
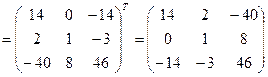
5. Найдем обратную матрицу
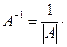
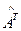
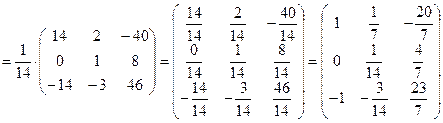
Произведем проверку. Для этого найдем произведения 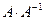 и
и 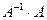 . Если окажется, что они равны
. Если окажется, что они равны 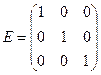 , то матрица
, то матрица 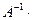 найдена верно.
найдена верно.
Имеем
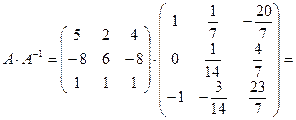
определим размер матрицы, которую получим в результате умножения: первая матрица имеет размер  , вторая −
, вторая −  . Берем количество строк у первой матрицы, а количество столбцов – у второй. Таким образом, получаем размер
. Берем количество строк у первой матрицы, а количество столбцов – у второй. Таким образом, получаем размер  .
.
Для того, чтобы найти элемент 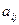 необходимо
необходимо 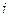 − ю строку первой матрицы умножить скалярно на
− ю строку первой матрицы умножить скалярно на 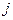 −й столбец второй матрицы
−й столбец второй матрицы
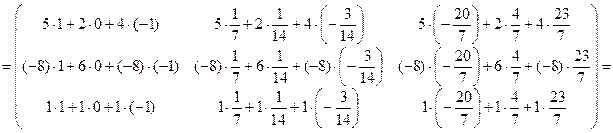
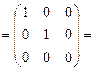
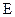 .
.
аналогично находим произведение 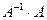 :
:
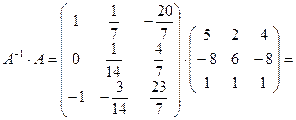
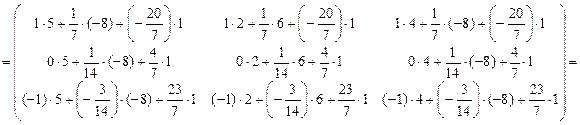
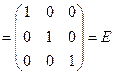
Ответ: 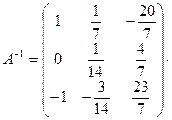
Пример 4. Даны координаты вершин пирамиды ABCD: A(10; 6; 6), B(- 2; 8; 2), C(6; 8; 9), D(7; 10; 3).
Найти:
Решение:
1) Если ребро АВ обозначить за вектор 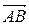 , то длина ребра - это длина вектора. Находим координаты вектора
, то длина ребра - это длина вектора. Находим координаты вектора 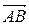 :
:
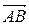 =(- 2-10; 8-6; 2-6)=(- 12; 2;- 4).
=(- 2-10; 8-6; 2-6)=(- 12; 2;- 4).
Если 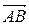 =(х; у: z), то его длина
=(х; у: z), то его длина 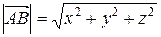 .
.
Следовательно,
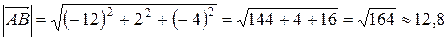 .
.
2) Угол между ребрами АВ и АD – это угол между векторами 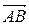 и
и 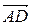 . Находим координаты вектора
. Находим координаты вектора 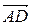 .
.
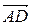 =(7-10; 10-6;3-6)=(-3;4;-3).
=(7-10; 10-6;3-6)=(-3;4;-3).
Из пункта 1) нам известны координаты вектора 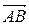 =(- 12; 2;- 4). Угол между двумя векторами находится по формуле:
=(- 12; 2;- 4). Угол между двумя векторами находится по формуле:
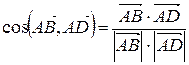 .
.
Если векторы 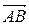 и
и 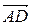 имеют координаты
имеют координаты 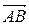 =(х1; у1: z1),
=(х1; у1: z1), 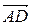 (х2; у2: z2) соответственно, то эта формула перепишется в виде:
(х2; у2: z2) соответственно, то эта формула перепишется в виде:
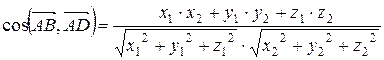 .
.
Следовательно, получаем
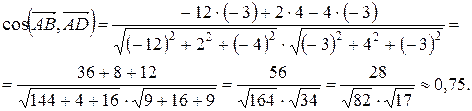
Итак, 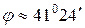 .
.
3) Уравнение прямой, проходящей через две точки М1(х1; у1; z1) и М2(х2; у2; z2) имеет вид:
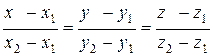

или равносильное ему уравнение:
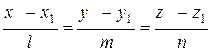 ,
,
где 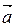 =(l,m,n) – координаты направляющего вектора прямой М1М2.
=(l,m,n) – координаты направляющего вектора прямой М1М2.
Направляющий вектор прямой – это вектор, параллельный прямой. В нашем случае прямая проходит через точки А(10; 6; 6) и В(- 2; 8; 2).Следовательно, уравнение прямой АВ:
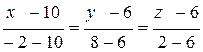 .
.
Итак, каноническое уравнение прямой АВ:
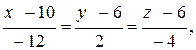
где направляющий вектор
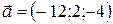
4) Уравнение плоскости по трем точкам находится по формуле:
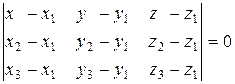 , (*)
, (*)
где А(х1; у1; z1); В (х2; у2; z2); С(х3; у3; z3) – точки, через которые проходит плоскость. Подставляя координаты точек А, В, С в формулу (*), получим:
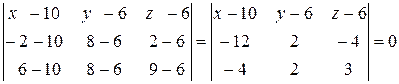 .
.
Считаем определитель, разложив его по первой строке.
D=а11А11+а12А12+а13А13,
где 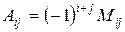 - алгебраические дополнения элементов
- алгебраические дополнения элементов 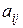 , а Мi j – минор элемента
, а Мi j – минор элемента 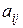 . Минором элемента матрицы называется определитель, получаемый (вычеркиванием строки и столбца, на пересечении которых он расположен) из данного. Следовательно,
. Минором элемента матрицы называется определитель, получаемый (вычеркиванием строки и столбца, на пересечении которых он расположен) из данного. Следовательно,
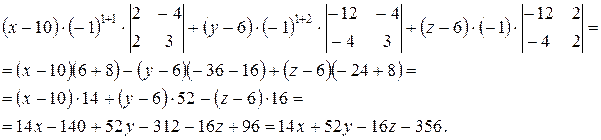
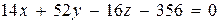 .
.
Итак, уравнение плоскости АВС:
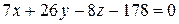 .
.
Пример 5. Дана система линейных уравнений:
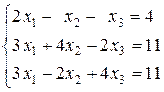
доказать ее совместность и решить тремя способами:
|
|
|
|
|
Дата добавления: 2014-11-07; Просмотров: 832; Нарушение авторских прав?; Мы поможем в написании вашей работы!