В результате получаем общее решение системы

.

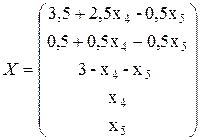Одно базисное решение получаем при x₄=x₅=0, т.е. x₁=3,5; x₂=0,5; x₃=3 или X₁=(3,5; 0,5; 3; 0; 0).

Чтобы получить другое базисное решение, достаточно задать x₄=1; x₅=0, тогда x₁=6; x₂=1; x₃=2 или X₂=(6; 1; 2; 1; 0).

Пример 6. Вычислить пределы функций, не пользуясь правилом Лопиталя:

а) ;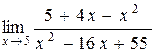

Функция 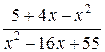не определена при х=5 и поэтому разрывна в этой точке. Числитель и знаменатель в точке х=5 обращается в нуль, налицо неопределенность 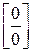. Выделим общий множитель (х-5) и сократим на него числитель и знаменатель, считая х ¹ 5, х ® 5.

.

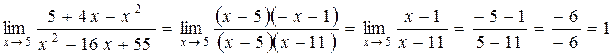б) ;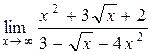

Ни числитель, ни знаменатель этой дроби не имеют конечного предела так как они неограниченно возрастают при неограниченном возрастании х, т. е. имеем дело с неопределенностью 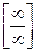. Поделим числитель и знаменатель дроби на х²:

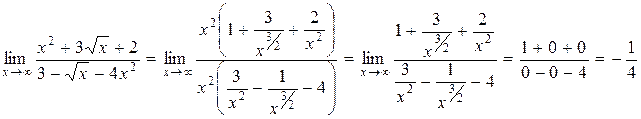
так как 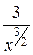, , 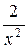, 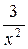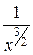при х ® ¥ – величины бесконечно малые.

в) ;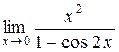

Поскольку числитель и знаменатель обращаются в нуль при х=0, то имеем дело с неопределенностью вида .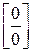

Воспользуемся тригонометрической формулой для преобразования знаменателя 2sin²x=1-cos2x и получим предел, в котором участвует тригонометрическая функция sinx.

Применив первый замечательный предел , получаем:

,

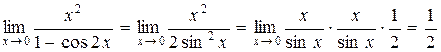так как 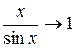при х ® 0.

г) .

Предел функции 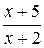при х ® 0 равен единице, т.е. в данном примере требуется раскрыть неопределенность 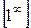. Примеры такого вида сводятся ко второму замечательному пределу .

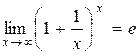Преобразуем выражение в скобках к виду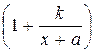

.

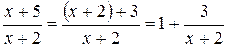Тогда

,

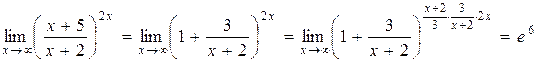т. к. , .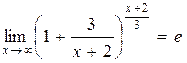

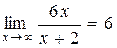Пример 7.

а) Найти производную функции .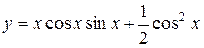

Решение:

Сначала преобразуем данную функцию: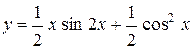

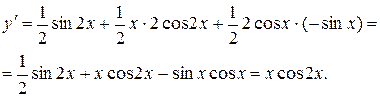
б) Найти производную функции .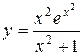

Решение:

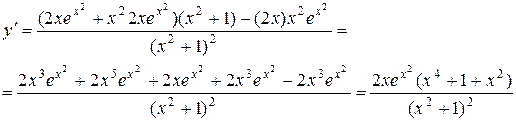
в) Найти производную функции .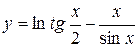

Решение:

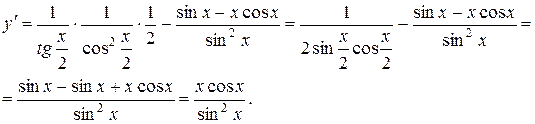
Пример 8. Исследовать функцию 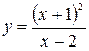и построить график.

Решение.

1. Данная функция не определена при 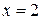, т. к. в этой точке знаменатель обращается в ноль. Значит

.

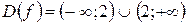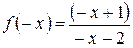
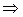
2. 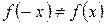, 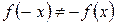. Следовательно, функция общего вида.

3. Не периодична.

4. Точки пересечения с осью Ох: 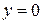при , 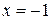. С осью Оу: ,

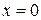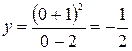. Нашли две точки пересечения графика функции с осями координат: и .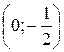

5. Исследуем на непрерывность. Точкой разрыва является .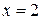

6. Из предыдущего пункта следует, что 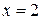- вертикальная асимптота.

Найдем наклонную асимптоту .

. .

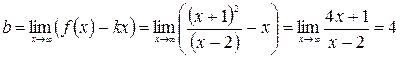Итак, 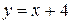- наклонная асимптота.

7. Исследуем на возрастание, убывание и экстремум функции. Для этого найдем производную функции.

.

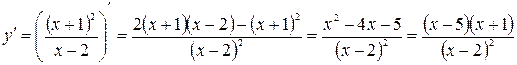Найдем точки, в которых производная равна нулю .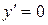

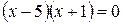
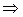
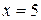и .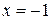

Далее отметим данные точки на числовой оси и к ним добавляем точку 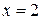, в которой 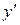не определена.

Находим интервалы, на которых 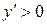: 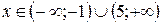и

: .

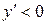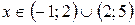При прохождении точки 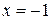производная меняет знак с плюса на минус. Следовательно, 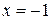- точка экстремума функции, а именно максимум.

.

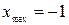
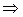
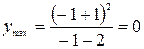При прохождении точки 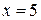производная меняет знак с минуса на плюс. Следовательно, 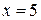так же является точкой экстремума функции, а именно минимумом.

.

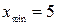
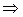
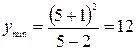8. Исследуем на вогнутость функции и точки перегиба. Для этого находим производную второго порядка.

.

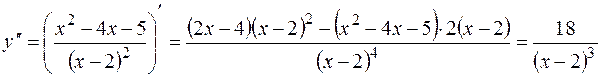Вторая производная в ноль никогда не обращается, поэтому на числовой оси отмечаем только .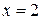

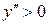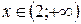: - функция вогнута и 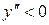: 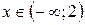- выпукла. Точек перегиба нет.

Составим таблицу, в которую занесем полученные сведения.

х		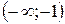-1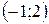
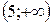
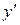
	+		-	не сущ.	-		+
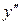
	-		-	не сущ.	+		+
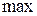
у				верт. ас.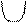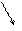

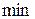
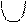
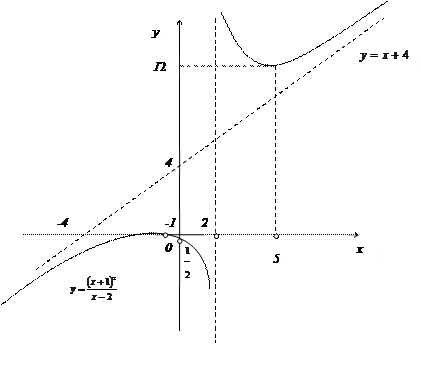
После того, как собрали все данные, полученные в ходе исследования, изобразим характерное поведение графика данной функции. (См. рис.).

Дата добавления: 2014-11-07