
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Примеры решения задач по теме. «Механические колебания и волны»
|
|
|
|
«Механические колебания и волны»
Задача 1. К невесомой пружине, коэффициент упругости которой 200 Н/м, прикреплен груз массой 1 кг. Груз смещен на 10 см от положения равновесия, после чего предоставлен себе. Определить наибольшее и наименьшее ускорения груза. Трением пренебречь.
Дано:
k = 200 Н/м
m = 1 кг
А0 = 10 см = 0,1 м
 amах -?; amin -?
amах -?; amin -?
Решение.
Под действием силы упругости груз совершает свободное гармоническое колебание, уравнение которого запишем в виде:
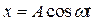 . (1)
. (1)
где А0 – амплитуда колебания, w – циклическая частота.
Продифференцировав выражение (1) по времени, определим скорость груза
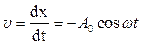 , (2)
, (2)
после дифференцирования скорости по времени определим ускорение:
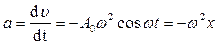 . (3)
. (3)
Так как
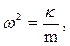 (4)
(4)
то:
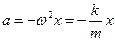 . (5)
. (5)
Ускорение имеет максимальное значение при x = A0, т.е. при наибольшем отклонении от положения равновесия:
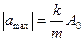 . (6)
. (6)
В положении равновесия при x = 0 ускорение 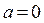 .
.
Проверка размерности расчетной формулы:
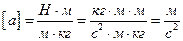 .
.
Подставляя числовые значения в выражение (6), получим:
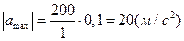 .
.
Ответ: наибольшее ускорение груза равно 20 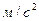 , наименьшее ускорение груза равно нулю.
, наименьшее ускорение груза равно нулю.
Задача 2. Материальная точка участвует одновременно в двух перпендикулярных гармонических колебаниях, уравнения которых:
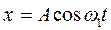 (1)
(1)
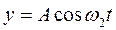 , (2)
, (2)
где А1 = 1 см; 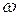 1 =
1 = 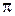 с-1; А2 = 2 см;
с-1; А2 = 2 см; 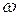 2 =
2 = 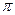 /2 с-1.
/2 с-1.
Найти уравнение траектории точки. Построить траекторию с соблюдением масштаба и указать направление движения точки.
Дано:
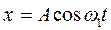 ;
;
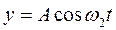
А1 = 1 см = 0,01м;
А2 = 2 см = 0,02м;
w1 = p с-1;
 w2 = p/2 с-1
w2 = p/2 с-1
y= f (х)?
Решение.
Чтобы определить траекторию точки, исключим время из уравнений (1) и (2). Заметив, что 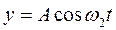 , применим формулу косинуса половинного угла:
, применим формулу косинуса половинного угла:
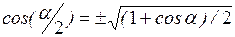 . (3)
. (3)
Используя это соотношение и отбросив размерности x и y, можно написать:
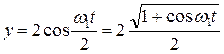 ;
;
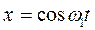 ,
,
откуда
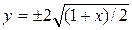 или
или 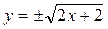 . (3)
. (3)
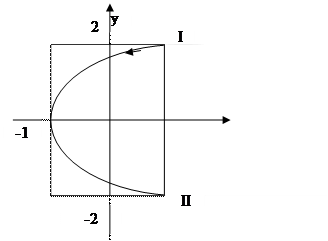
Выражение (3) есть уравнение параболы, ось которой совпадает с осью ОХ. Как показывают уравнения (I) и (2), амплитуда колебаний точки по оси OX равна 1, а по оси ОУ - 2. Следовательно, абсциссы всех точек траектории заключены в пределах от -1 до +1, а ординаты – от -2 до + 2. Для построения траектории найдем по уравнению (3) значения y, соответствующие ряду значений x удовлетворявших условию 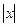
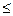 1:
1:
 |
x y = 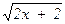 х y =
х y = 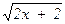
 |
- 1 0 0 ± 1,41
- 0,75 ± 0,71 0,5 ± 1,73
- 0,5 ± 1  1 ± 2
1 ± 2
1 x
-1
Рис.
Начертив координатные оси и выбрав единицу длины - сантиметр, построим точки. Соединив их плавной кривой, получим траекторию результирующего колебания точки, та представляет собой часть параболы, заключенной внутри прямоугольника амплитуд.
Далее определим направление движения точки. Из уравнений (1) и (2) находим, что период колебаний точки по горизонтальной оси Тх = 2 с, а по вертикальной оси Ту = 4 с.
Следовательно, когда точка совершает одно полное колебание по оси ОХ, она совершает только половину полного колебания по оси OY. В начальный момент (t = 0) имеем: х = 1, у = 2 (точка находится в положении 1). При t = 1 с получим: х = -1 и у = 0 (точка находится в вершине параболы). При t = 2 с получим: х = 1 и у = -2 (точка находится в положении 2). После этого она будет двигаться в обратном направлении.
Ответ: уравнение движения точки 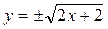 есть уравнение параболы; траектория движения точки изображена на рисунке.
есть уравнение параболы; траектория движения точки изображена на рисунке.
Задача 3. Плоская волна распространяется в упругой среде со скоростью 100 м/с. Наименьшее расстояние между точками среды, фазы колебаний которых противоположны, равно 1 м. Определить период колебаний и частоту.
Дано:
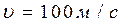 ;
;
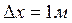
__________________
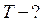
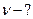
Решение.
Точки, находящиеся друг от друга на расстоянии, равном длине волны, колеблются с разностью фаз, равной 2p. Точки, находящиеся друг от друга на любом расстоянии, колеблются с разностью фаз, равной
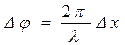 (1)
(1)
Решая это равенство относительно l, получаем:
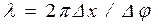 (2)
(2)
По условию задачи D j = p.
Подставляя значения величин, входящих в выражение (2), получим:
 .
.
Скорость u распространения волны связана с длиной волны l и периодом колебаний Т отношением:
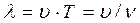 , (3)
, (3)
где 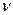 – частота колебаний
– частота колебаний
Из выражения (3) определяем частоту колебаний:
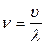 .
.
Период колебаний
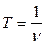 .
.
Проверка размерности расчетных формул:
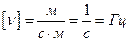 ;
; 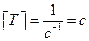 .
.
Вычисление: 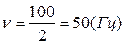 ;
;
Ответ: частота колебаний равна 50 Гц, период колебаний равен 0,02 с.
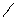
 Задача 4. Тонкое кольцо радиуса R совершает малые колебания около точки О (рис.). Найти период колебаний, если они происходят в плоскости рисунка.
Задача 4. Тонкое кольцо радиуса R совершает малые колебания около точки О (рис.). Найти период колебаний, если они происходят в плоскости рисунка.
 |
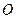 Дано: R - радиус кольца
Дано: R - радиус кольца


 _____________________
_____________________
T -?
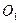 | ||||
 | ||||
 | ||||
Рис.
Решение.
При отклонении центра кольца от вертикали, проходящей через точку подвеса (рис.) на небольшой угол 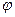 (
(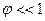 ) на кольцо действует момент силы тяжести, возвращающий его в положение равновесия.
) на кольцо действует момент силы тяжести, возвращающий его в положение равновесия.
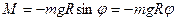 . (1)
. (1)
Основное уравнение динамики твердого тела выглядит в данном случае следующим образом:
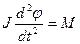 , (2)
, (2)
где М - момент силы тяжести, J – момент инерции кольца относительно точки O.
Согласно теореме Штейнера
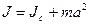 (3)
(3)
где 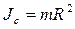 – момент инерции кольца относительно оси, проходящей через его центр масс перпендикулярно плоскости кольца;
– момент инерции кольца относительно оси, проходящей через его центр масс перпендикулярно плоскости кольца; 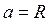 .
.
Следовательно,
 (4)
(4)
Подставляя (1) и (4) в (2), получим:
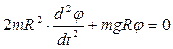 , (5)
, (5)
откуда приходим к уравнению малых колебаний кольца:
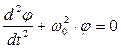 , (6)
, (6)
где
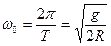 - круговая частота колебаний. (7)
- круговая частота колебаний. (7)
Из формулы (7) выражаем период колебания кольца:
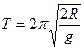 .
.
Проверка размерности: [T]= 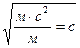
Ответ: период колебаний кольца 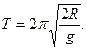
Задача 5. Наблюдатель, стоящий на станции, слышит гудок проходящего электровоза. Когда электровоз приближается, частота звуковых колебаний гудка равна 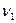 , а когда удаляется -
, а когда удаляется - 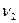 . Принимая, что скорость звука известна, определить: 1) скорость
. Принимая, что скорость звука известна, определить: 1) скорость 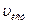 электровоза;
электровоза;
2) собственную частоту 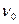 колебаний гудка.
колебаний гудка.
Дано:
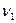 - частота воспринимаемого сигнала при приближении электровоза;
- частота воспринимаемого сигнала при приближении электровоза;
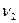 - частота воспринимаемого сигнала при удалении электровоза;
- частота воспринимаемого сигнала при удалении электровоза;
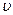 - скорость звука.
- скорость звука.
________________
1) 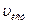 -?
-?
2) 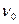 -?
-?
Решение.
Согласно формуле, выражающей частоту 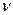 воспринимаемого сигнала в эффекте Доплера:
воспринимаемого сигнала в эффекте Доплера:
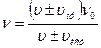 , (1)
, (1)
где 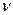 - частота звука, воспринимаемая движущимся приемником;
- частота звука, воспринимаемая движущимся приемником;
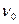 - частота звука, посылаемого источником;
- частота звука, посылаемого источником;
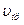 - скорость движения приемника звука;
- скорость движения приемника звука;
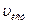 - скорость движения источник звука;
- скорость движения источник звука;
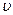 - скорость звука.
- скорость звука.
По условию задачи скорость приемника 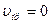 , следовательно,
, следовательно,
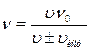 , (2)
, (2)
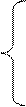
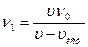 (электровоз приближается к наблюдателю); (3)
(электровоз приближается к наблюдателю); (3)
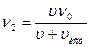 (электровоз удаляется от наблюдателя). (4)
(электровоз удаляется от наблюдателя). (4)
Из уравнений (3) и (4) выражаем скорость источника звука:
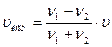 . (5)
. (5)
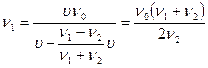 , (6)
, (6)
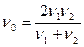 . (7)
. (7)
Ответ: скорость электровоза 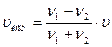 ,
,
собственная частота колебаний гудка 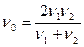 .
.
|
|
|
|
|
Дата добавления: 2014-11-07; Просмотров: 3222; Нарушение авторских прав?; Мы поможем в написании вашей работы!