Примеры решения задач по теме

«Волновые свойства света»

Задача 1. Расстояние между двумя когерентными источниками равно 0,9 мм. Источники, испускающие монохроматический свет с длиной волны 640 нм, расположены на расстоянии 3,5 м от экрана. Определить число светлых полос, располагавшихся на 1 см длины экрана.

Дано: λ = 640 нм = 64∙10^{-8 м} ;

d = 0,9 мм = 9∙10^{-4 м;}

L = 3,5 м.

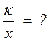
Решение.

В точке О на экране (рис.) будет максимальная освещенность: точка О равноудалена от обоих источников S'₁ и S'₂, поэтому разность хода волн, S'₁ О и S'₂ О равна нулю. В произвольной точке экрана О_к максимум освещенности будет наблюдаться, если оптическая разность хода когерентных волн равна целому числу длин волн:

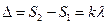(1)

где S₂, S₁ – оптические пути интерферирующих волн; l – длина волны падающего света; к – номер светлой полосы (центральная светлая полоса принята за нулевую).

Оптическая разность хода волн

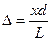, (2)

где x – расстояние от центральной светлой полосы до к -й светлой полосы.

О_к

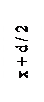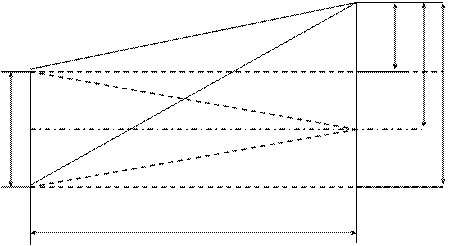S₁

S^’₁

O₁

d S₂ О

S^’₂ O₂

L

Рис.

Учитывая выражение (1), получим:

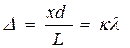(3) Из выражения (3) определяем число светлых интерференционных полос на единицу длины:

.

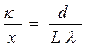Произведем вычисления:

,

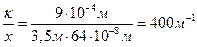Следовательно, число светлых полос, располагавшихся на 1 см длины экрана, равно 4.

Ответ: на один сантиметр экрана приходится 4 светлые полосы.

Задача 2. Для устранения отражения света от поверхности линзы на нее наносится тонкая пленка вещества с показателем преломления 1,26, меньшим, чем у стекла (просветление оптики). При какой наименьшей толщине пленки отражение света с длиной волны 0,55 мкм не будет наблюдаться, если угол падения лучей 30⁰?

Дано:

n = 1,26;

λ = 0,55 мкм =5,5 ∙ 10^{-7 м}

n₁

i₁ = 30⁰

n₂ n₁

d =?

Рис.

Решение.

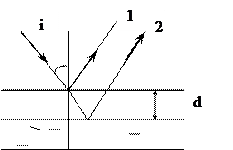
Оптическая разность хода лучей, отраженных от верхней и нижней поверхностей пленки (рис.)

D = 2 d 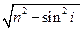, (1)

где d – толщина пленки; n – показатель преломления пленки; i – угол падения лучей.

В выражении (1) учтено, что отражение лучей на верхней и нижней поверхностях пленки происходит от оптически более плотной среды, поэтому потери полуволны в обоих случаях компенсируют друг друга.

Условие интерференционного минимума

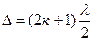(2)

Из (1) и (2) находим:

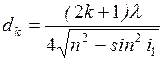(3)

Полагая к = 0,1,2,3...., получим ряд возможных значений толщины пленки. Минимальной толщине пленки соответствует к = 0.

Подставим в расчетную формулу (3) числовые значения входящих величин и произведем вычисления:

.

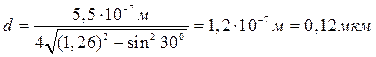Ответ: наименьшая толщина пленки равна .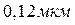

Задача 3. Радиус второго темного кольца Ньютона в отраженном свете 0,4 мм. Определить радиус кривизны плосковыпуклой линзы, взятой для опыта, если она освещается монохроматическим светом с длиной волны 0,64 мм.

Дано:

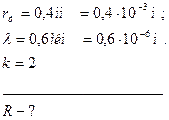Кольца Ньютона — кольцеобразные интерференционные максимумы и минимумы, появляющиеся вокруг точки касания слегка изогнутой выпуклой линзы и плоскопараллельной пластины при прохождении света сквозь линзу и пластину (рис.). Простая интерференционная картина возникает в тонкой прослойке воздуха между стеклянной пластиной и положенной на нее плосковыпуклой линзой, сферическая поверхность которой имеет большой радиус кривизны. Эта интерференционная картина имеет вид концентрических колец, получивших название кольца Ньютона.

Волна 1 (рис.) появляется в результате отражения от выпуклой поверхности линзы на границе стекло — воздух, а волна 2 — в результате отражения от пластины на границе воздух — стекло. Эти волны когерентны, то есть они имеют одинаковую длину и постоянную разность фаз, которая возникает из-за того, что волна 2 проходит больший путь, чем волна 1. Если вторая волна отстает от первой на целое число длин волн, то, складываясь, волны усиливают друг друга. Напротив, если вторая волна отстает от первой на нечетное число полуволн, то колебания, вызванные ими, будут происходить в противоположных фазах и волны гасят друг друга. При этом радиус темного кольца

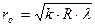, (1)

где R — радиус кривизны линзы; k = 0, 1, 2, …; λ — длина волны света в вакууме;

Из формулы (1) выражаем радиус кривизны линзы:

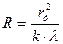. (2)

Проверка размерности расчетной формулы:

.

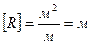Произведем вычисление:

,

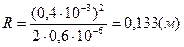Ответ: радиус кривизны плосковыпуклой линзы равен 0,133 м.

Задача 4.На дифракционную решетку длиной 10 мм, имеющую 400 штрихов на 1 мм, падает нормально свет от разрядной трубки. Помещенная вблизи решетки линза проецирует дифракционную картину (рис.) на плоский экран Э, удаленный от линзы на расстояние 1м. Определить:

1) ширину спектра первого порядка, если границы видимого спектра составляют 780 нм (красный край спектра) и 400 нм (фиолетовый край спектра);

2) число спектральных линий красного цвета, которые теоретически можно наблюдать с помощью данной дифракционной решетки;

3) в спектре какого порядка эта решетка может разрешить две линии с длиной волны, равной 500 нм и 500,1 нм

l₀

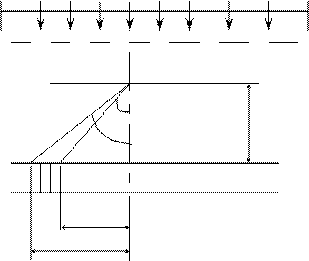линза

^φ₁ L

^φ₂

Э

l₁

l₂

Рис.

Дано: l₀ = 10 мм = 10^{-2 м} ;

N = 4^.10⁵;

L = 1 м;

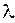_кр = 780 нм = 7,8 ^. 10^{-7 м} ;

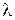_ф = 400 нм = 4^.10^{-7 м} ;

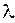₁ = 500 нм = 5^.10^{-7 м} ;

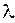₂ = 500,1 нм = 5,001^.10^{-7 м} .

l₁ =?; к _кр =?; к =?

Решение.

Угол j отклонения лучей, соответствующий максимуму фиолетового цвета при дифракции света на решетке, определяется из условия:

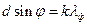(1)

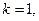следовательно,

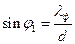. (2)

Аналогично, для дифракционного максимума красного цвета получим:

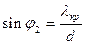. (3)

Из рисунка следует, что расстояние от центра дифракционной картины до фиолетовой спектральной линии равно

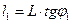. (4)

Соответственно, для красной спектральной линии

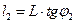(5)

Ширина спектра первого порядка будет

,

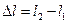или с учетом (4), (5):

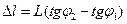(6)

В случае малых углов 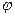для спектра первого порядка справедливо выражение:

.

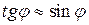Поэтому, подставив выражения (2) и (3) в формулу (6), получим:

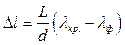(7)

Зная число штрихов N на 1 мм решетки, найдем период решетки:

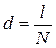. (8)

Подставляя (8) в формулу (7), получим:

,

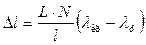где 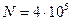- число штрихов, приходящихся на 1 метр решетки

Произведем вычисления:

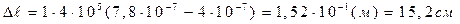
Для определений числа спектральных линий красного цвета найдем максимальное значение к_mах., исходя из того, что максимальный угол отклонения лучей не может превышать 90° ().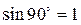

Из формулы (1) имеем:

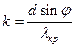. (9)

Следовательно,

.

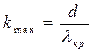С учетом (8), получим:

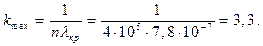
Так как число к_mах должно быть обязательно целым, то к_mах =3. Влево и вправо от центра картины будет наблюдаться одинаковое число спектральных линий, равное 2к_mах. Таким образом, общее число спектральных линий равно 2к_mах = 6.

Так как разрешающая способность дифракционной решетки

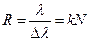, (10)

то минимальная разница длин волн двух спектральных линий, разрешаемых решеткой 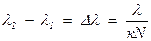. (11)

Две спектральные линии разрешены, если

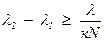. (12)

Подставляя (11) в (12) и, учитывая, что l = l₁ , получаем:

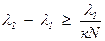. (13) Из выражения (13) следует, что спектральные линии разрешены в спектрах с порядком

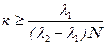. (14)

Произведем вычисления:

Дата добавления: 2014-11-07