Волновые процессы

Явление резкого возрастания амплитуды вынужденных колебаний при приближении частоты вынуждающей силы к частоте, равной или близкой к собственной частоте колебательной системы, называется резонансом, а соответствующая частота – резонансной частотой.

Чтобы найти 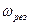, нужно найти максимум функции (1) или минимум выражения, стоящего под корнем в знаменателе, т.е. .

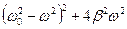Продифференцируем это выражение по и приравняем нулю, получим условие, определяющее :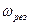

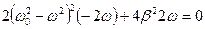или .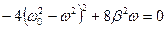

Это уравнение имеет корн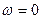и: и 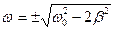. Решение 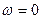соответствует максимуму знаменателя. Отрицательное значение следует отбросить, как не имеющее физического смысла. Таким образом, для 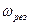получаем: 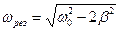(3).

Подставив это значение в формулу для А (1) получим выражение для резонансной амплитуды:

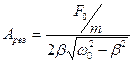(4).

Из этой формулы следует, что при отсутствии сопротивления среды амплитуда при резонансе обращалась в 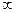. Согласно (3), 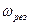при тех же условиях (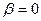) совпадает с собственной частотой .

Из рисунка видно, что чем меньше 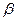, тем выше и правее лежит максимум данной кривой. При очень большом затухании (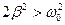) выражение для 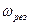становится мнимым. Это означает, что при данных условиях резонанса не наблюдается: с увеличением амплитуда монотонно убывает.

При малом затухании (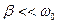), как видно из (4), амплитуда при резонансе приближенно равна: .

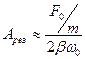Разделим это выражение на смещение 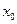от положения равновесия под действием постоянной силы 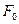, равное 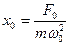. В результате получим

.

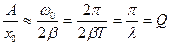Таким образом, добротность Q показывает: во сколько раз амплитуда в момент резонанса превышает смещение системы из положения равновесия под действием постоянной силы той же величины, что и амплитуда вынуждающей силы.

Волной (или волновым процессом) называют процесс распространения колебаний в упругой среде.

Колебание – процесс, в той или иной степени повторяющийся во времени.

Тело называется упругим, а его деформации при внешних воздействиях – упругими деформациями, если они полностью исчезают после прекращения этих воздействий. Согласно закону Гука, упругие деформации прямо пропорциональны вызывающим их внешним воздействиям. При достаточно малых воздействиях почти все тела можно считать упругими.

Упругие свойства тел зависят от характера теплового движения молекул и сил их взаимодействия. Например, газообразное тело беспрепятственно изменяет свою форму в соответствии с формой занимаемого сосуда – т.е. газ не обладает упругостью формы. В то же время газу присуща объемная упругость – т.е. способность сопротивляться изменению его объема. По закону Гука для объемной упругости, изменение давления 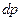газа при малом изменении его объема 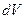прямо пропорционально относительной объемной деформации: .

Твердые тела обладают упругостью формы и объемной деформацией (упругость формы проявляется в их сопротивлении деформации сдвига).

Сдвигом называется такая деформация твердого тела, при которой все его плоские слои, параллельные некоторой неподвижной плоскости, называемой плоскостью сдвига, не искривляясь и не изменяясь в размерах, смещаются параллельно друг другу.

В первом приближении, все среды (за исключением разреженных газов) можно считать абсолютно упругими, так как внутренние силы, возникающие в них при достаточно малых деформациях, оказываются пропорциональными деформациям.

Если в каком либо месте упругой среды возбудить колебание ее частиц, то вследствие взаимодействия между частицами это колебание будет распространяться в среде от частицы к частице. При этом частицы среды, в которой распространяется волна, не вовлекаются волной в поступательное движение, они лишь совершают колебания относительно своих равновесных положений.

Поэтому основным свойством всех волн, независимо от их природы, является перенос энергии без переноса вещества.

Различают продольные и поперечные волны. В продольной волне частицы колеблются вдоль направления распространения волны, в поперечной волне– перпендикулярно направлению ее распространения.

Упругие поперечные волны могут возникнуть лишь в среде, обладающей сопротивлением к сдвигу. Поэтому в жидкой и газообразной средах возникают только продольные волны, в твердой среде возможно возникновение как продольных, так и поперечных волн.

Распространяясь от источника колебаний, волновой процесс охватывает новые части пространства. Геометрическое место точек, до которых доходят колебания к моменту времени t, называют фронтом волны (или волновым фронтом). Фронт волны представляет собой ту поверхность, которая отделяет часть пространства, вовлеченного в волновой процесс, от области, в которой колебания еще не возникли.

Геометрическое место точек, колеблющихся в одинаковой фазе 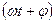, называют волновой поверхностью. Волновую поверхность можно провести через любую точку пространства, охваченного волновым процессом, т.е. волновых поверхностей существует бесконечное множество, тогда как волновой фронт в каждый момент времени один.

Волновые поверхности могут быть любой формы. Если волновые поверхности представляют собой параллельные плоскости – то волну называют плоской, если совокупность концентрических сфер – сферической.

Упругую волну называют гармонической, если соответствующие ей колебания частиц среды являются гармоническими.

Если рассмотреть гармоническую поперечную волну, распространяющуюся вдоль ось 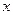со скоростью 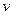, то график зависимости между смещением 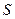частиц и расстоянием 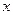этих частиц от источника колебаний О для какого-либо фиксированного момента времени имеет вид:

Такой график можно строить как для поперечной, так и для продольной волны. Расстояние λ, на которое распространяется волна за время 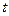, равное периоду колебаний частиц среды, называют длиной волны. Из рисунка видно, что 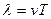( 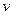- скорость волны, зависящая от плотности среды 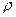и модуля Юнга 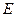(если волны продольные) или модуля сдвига 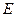(если волны поперечные), 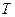- период (время одного колебания)).

Дата добавления: 2014-11-07