Задачи 1-10

КОНТРОЛЬНАЯ РАБОТА №1

К ВЫПОЛНЕНИЮ КОНТРОЛЬНЫХ РАБОТ

МЕТОДИЧЕСКИЕ УКАЗАНИЯ

V. Интегральное исчисление

19.Понятие первообразной; неопределенного интеграла. Таблица основных интегралов. Методы интегрирования: непосредственное, замена переменной, по частям. Интегрирование рациональных дробей.

20.3адачи, приводящие к понятию определенного интеграла. Понятие определенного интеграла, как предела интегральных сумм. Теорема существования. Свойства определен­ного интеграла. Связь определенного интеграла с неопределенным. Формула Ньютона-Лейбница. Методы интегрирования для определенного интеграла. Приложение определенного интеграла к решению задач.

21. Понятие несобственных интегралов с бесконечными пределами интегрирования и от неограниченных функций. Понятие сходящихся и расходящихся интегралов. Интеграл Пуас­сона. Геометрический смысл сходящихся несобственных интегралов.

Литература

1. Высшая математика для экономистов. Под редакцией проф. Н. Ш. Крамера. – М.: Юнити, 2001

2. Баврин. И. И. Высшая математика. М.: Академия, 2002

3. Зайцев И. А. Высшая математика. Учебное пособие для неинженерных специальностей с.-х. Вузов. – М.: Высшая школа, 1991

4.Шипачев В. С. Высшая математика– М.: Высшая школа, 1996

5. Лихолетов И. И. Высшая математика, теория вероятностей и математическая статистика. Минск. Высшая школа, 1976

6. Карасев А. И., Аксютина З. М., Савельева Т. И.. Высшая математика для экономических ВУЗов – ч. 1 – М.: Высшая школа, 1982

7. Минорский В. П. сборник задач по высшей математике. –М.: Наука, 1987

8. Данко П. Е., Попов А. Г.- ч. 1,2 - М.: Высшая школа, 1974

В предлагаемых методических указаниях решены задачи, анало­гичные тем, которые даются студентам-заочникам в контрольных ра­ботах; обращено внимание на основные трудности и типичные ошиб­ки, которые допускаются при выполнении контрольных работ.

Перед решением каждой задачи предлагаем ознакомиться с ос­новными вопросами теории. Перечисленные ниже вопросы по каждой теме являются основными при защите контрольных работ.

Первая контрольная работа посвящена темам: «Аналитическая геометрия на плоскости», «Введение в математический анализ»,

«Дифференциальное исчисление функции одной переменной», «Дифференциальное исчисление функции с двумя переменными», «Интегральное исчисление».

Предварительно ознакомьтесь со следующими вопросами по теме «Аналитическая геометрия на плоскости»:

1. Метод координат на плоскости. Расстояние между двумя точ­ками на плоскости А(х₁;у₁) и В(х₂;у₂):

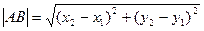
2. Деление отрезка пополам (нахождение середины отрезка):

;

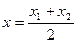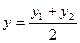
3. Угловой коэффициент прямой: k = tgα, где α- угол наклона прямой к оси ОХ, 0 ≤ α < π

4. Уравнение прямой с угловым коэффициентом: у = kx+b.

5. Уравнение прямой, проходящей через заданную точку (х_о;у_о) в данном направлении (уравнение пучка прямых):

у - у_о = k (х - х_о).

6. Уравнение прямой, проходящей через две заданные точки (х₁;у₁) и (х₂;у₂): _,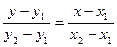

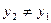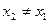
7. Общее уравнение прямой Ах + By + С = 0, его частные случаи: Ах+Ву=0, Ах+В=0, Ву+С=0.

8. Угол между двумя прямыми:

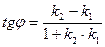
где k₁ и k₂ - угловые коэффициенты данных прямых.

9. Условие параллельности двух прямых: k₁ =k₂.

10. Условие перпендикулярности двух прямых:

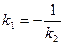
11. Расстояние от точки 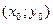до прямой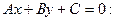

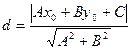
Обратите внимание, что уравнение прямой, в каком бы виде оно ни было записано, является уравнением первой степени.

Задача. Даны вершины треугольника А(2;1), В(-4;4), С(-1,5). Сделать чертеж и найти:

1) длину стороны АВ;

2) внутренний угол А в радианах с точностью до 0,001;

3) уравнение высоты CD, проведенной через вершину С;

4) уравнение медианы BE, проведенной через вершину В;

5) точку пересечения высоты CD и медианы BE;

6) длину высоты, опущенной из вершины С.

Решение. Начнем решение задачи с выполнения чертежа (рис 1).

Построим точки А(2;1), В(-4;4), С(-1;5) в прямоугольной сис­теме координат и, соединив их отрезками прямых, получим тре­угольник ABC. Проведем высоту CD и медиану BE, уравнения кото­рых нужно найти.

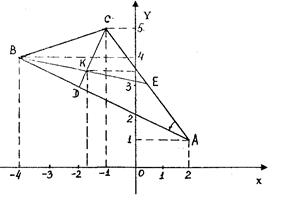
Рис. 1

1. Длину стороны АВ находим как расстояние между двумя точ­ками А(2;1) и В(-4;4) по формуле:

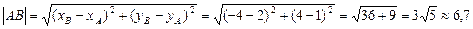2. При ответе на вопрос пункта 2 (найти внутренний угол) вос­пользуемся чертежом. Отметим искомый угол А дугой и на ней по­ставим стрелку, показывающую направление, противоположное дви­жению часовой стрелки. Первой будет та прямая, от которой, направлена стрелка. Так, на рис. 1 первая прямая АС, вторая - АВ.

Следовательно, в формуле надо положить 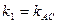и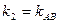

Найдем указанные угловые коэффициенты прямых. Для этого нет необходимости составлять их уравнения, проще воспользоваться формулой, где угловой коэффициент прямой находится по координа­там двух ее точек.

Так, в нашем примере:

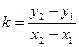
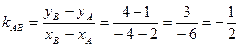
тогда

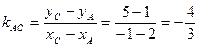
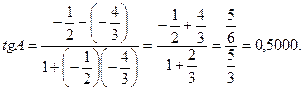
Заметим что tg A > 0, так как угол А - острый.

Из таблицы (например, Брадиса) видно, что такое значение тан­генса соответствует углу А=26°34^/.

Обратите внимание на то, что ответ следует дать в радианах. Для перевода градусов в радианы можно воспользоваться соответствую­щими таблицами, либо формулой:

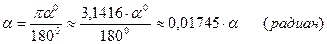
α - угол в градусах.

Итак, в радианах угол 3. Составим уравнение высоты CD. Высота CD перпендикулярна стороне АВ. Угловой коэффициент прямой АВ был найден ранее:

k_AВ = -1/2

По условию перпендикулярности двух прямых

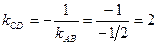
Уравнение высоты СD cоставим по известной точке С (-1;5)

найденному угловому коэффициенту, воспользовавшись урав-

нением 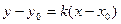; пучка прямых: .

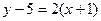Ответ обычно дают в виде уравнения с целыми коэффициентами и с правой частью, равной нулю. Преобразуем полученное уравнение:

;

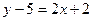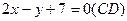
Замечание. Возьмите себе за правило проверять полученные результаты, причем это следует делать не простым повторением проделанных действий, а каким-либо другим способом. Например, полученное уравнение высоты СD проверьте, подставив в него координаты точки С, при этом должно получиться тождество.

Действительно: 2 (- 1) – 5 + 7 = 0.

4. Уравнение медианы ВЕ, проведенной из вершины В, составляется по координатам двух точек В и Е. Координаты точки В известны, а координаты точки Е находим как координаты середины отрезка АС по формулам деления отрезка пополам: ;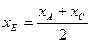

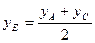
В рассматриваемой задаче

;

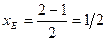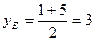
Имея две точки В(-4;4) и Е (1/2;3) Запишем уравнение ВЕ:

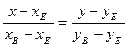
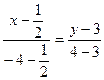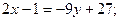
а именно: ; 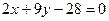(BE)

5. Координаты точки пересечения высоты СD и медианы ВЕ найдем, решив систему уравнений СD и ВЕ:

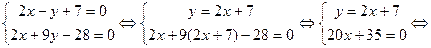
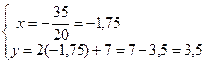
Итак, К(-1,75; 3,5), что соответствует чертежу на рис. 1.

б.Длина высоты СD есть расстояние от вершины С до стороны АВ. Поэтому длину высоты находим по формуле расстояния от точки 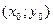до прямой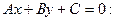

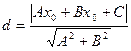
В данной задаче С (-1;5), а уравнение стороны АВ можно составить, используя уравнение пучка прямых:

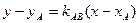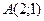, где и

Тогда

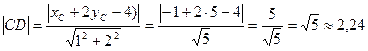
Дата добавления: 2014-11-07