
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Задачи 21-30
|
|
|
|
 По теме «Введение в анализ» рассмотрите предварительно следующие вопросы о функциях и пределах:
По теме «Введение в анализ» рассмотрите предварительно следующие вопросы о функциях и пределах:
1. Понятие функции, способы задания функции, область ее определения.
2. Основные элементарные функции, их свойства и графики.
3. Понятие предела функции в точке.
4. Понятие бесконечно малой функции 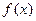 и ее свойства:
и ее свойства: 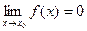
5. Понятие бесконечно большой функции 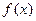 :
:
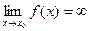
ее свойства и связь с бесконечно малой функцией.
6. Теоремы о пределах: предел суммы, разности, произведения, частного функций.
7.Первый замечательный предел:
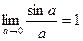 или
или 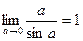
8. Второй замечательный предел:
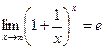
или в другой форме:

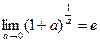
где e - иррациональное число: 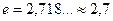 .
.
9. Эквивалентные бесконечно малые функции.
10. Виды неопределенностей и способы их раскрытия:
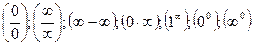
11. Понятие непрерывности функции в точке и на промежутке.
12. Теоремы о непрерывных функциях.
Задача. Найти пределы функций:
1. 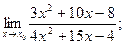 2.
2. 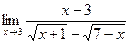

При 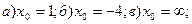
3. 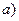
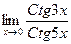
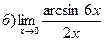
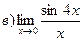 4.
4. 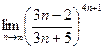
Решение. Прежде всего заметим, что во всех примерах следует найти предел частного. Как известно, предел частного существует и равен частному пределов, если существуют пределы числителя и знаменателя и предел знаменателя не равен нулю.
1.а) 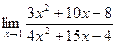
Предел числителя и предел знаменателя дроби найдем, подставив в них предельное значение аргумента:
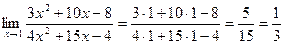
Здесь теорема о пределе частного применима.
б) 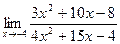
При подстановке 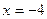 в числитель и знаменатель дроби убеждаемся, что их пределы равны нулю. Теорема о пределе частного здесь не применима. В данном случае говорят, что имеется неопределенность вида «ноль на ноль»
в числитель и знаменатель дроби убеждаемся, что их пределы равны нулю. Теорема о пределе частного здесь не применима. В данном случае говорят, что имеется неопределенность вида «ноль на ноль» 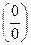
Такая неопределенность раскрывается сокращением дроби на бесконечно малую функцию 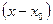 , в данном случае на
, в данном случае на 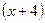 , которая обращает числитель и знаменатель в нуль. Для этого нужно сначала разложить на множители числитель и знаменатель дроби.
, которая обращает числитель и знаменатель в нуль. Для этого нужно сначала разложить на множители числитель и знаменатель дроби.
Напомним формулу разложения квадратного трехчлена на множители: 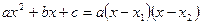 , где
, где 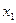 и
и 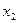 -корни квадратного трех-
-корни квадратного трех-
члена, которые находим из уравнения 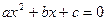 .
.
Разложим на множители числитель данной дроби:
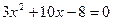 ;
; 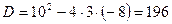
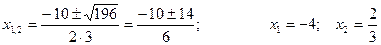
Следовательно: 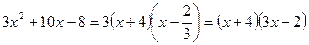
Разложим на множители знаменатель дроби:
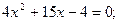
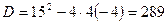 ;
;
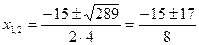
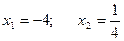
Следовательно: 4х2+15х-4=4(х+4)(х-1 /4)=(х+4)(4х-1).
Тогда 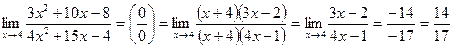 в)
в) 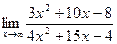
При 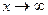 числитель и знаменатель дроби также стремятся к бесконечности. В этом случае теорема о пределе частного неприменима. Говорят, что имеется неопределенность вида «бесконечность на бесконечность»
числитель и знаменатель дроби также стремятся к бесконечности. В этом случае теорема о пределе частного неприменима. Говорят, что имеется неопределенность вида «бесконечность на бесконечность» 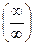
Чтобы ее раскрыть, каждый член числителя и знаменателя дроби разделим на 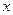 в наивысшей для данного примера степени (то есть на
в наивысшей для данного примера степени (то есть на  ), от чего величина дроби не изменится. Тогда получим:
), от чего величина дроби не изменится. Тогда получим:
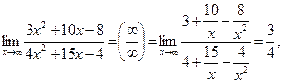
так как 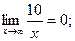
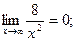
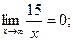
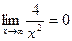
Замечание. Полезно заметить и запомнить, что предел отношения многочленов при 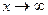 равен отношению их коэффициентов при старших степенях.
равен отношению их коэффициентов при старших степенях.
2. 
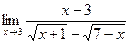
При подстановке предельного значения 
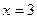 в числитель и знаменатель дроби убеждаемся, что их пределы равны нулю. Таким образом, перед нами вновь неопределенность вида
в числитель и знаменатель дроби убеждаемся, что их пределы равны нулю. Таким образом, перед нами вновь неопределенность вида
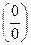
которая раскрывается сокращением дроби на бесконечно малую функцию 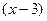 . Для этого предварительно умножим числитель и знаменатель дроби на выражение, сопряженное иррациональному выражению в знаменателе, то есть на
. Для этого предварительно умножим числитель и знаменатель дроби на выражение, сопряженное иррациональному выражению в знаменателе, то есть на 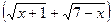 :
:
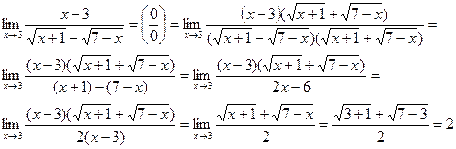
При умножении сопряженных выражений в знаменателе было использовано тождество 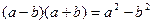
З.Для решения примеров под номером 3 используется первый замечательный предел, с помощью которого раскрываются некоторые неопределенности вида 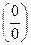
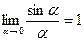
Примеры этого пункта можно решать также с помощью эквивалентных бесконечно малых функций. Две бесконечно малые функции 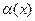 и
и 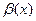 называются эквивалентными в точке
называются эквивалентными в точке 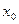 , если предел их отношения в этой точке равен 1:
, если предел их отношения в этой точке равен 1:
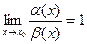
значит 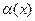 ~
~ 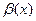 при
при 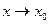
Например, при 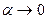 :
: 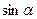 ~
~ 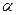 ;
; 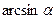 ~
~ 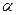 ;
;
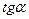 ~
~ 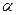 ;
; 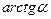 ~
~ 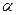 .
.
При вычислении пределов бесконечно малые множители можно заменять на эквивалентные им.
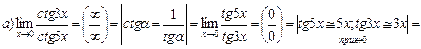
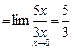
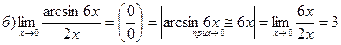
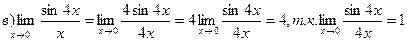
4.Для раскрытия неопределенностей вида (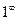 ) применяется второй замечательный предел:
) применяется второй замечательный предел:
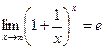
где e - иррациональное число, то есть бесконечная непериодическая десятичная дробь, ее приближенное значение: e ≈ 2,7
Найдем 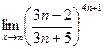
Очевидно, что 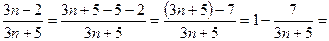
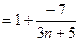
Тогда
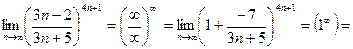
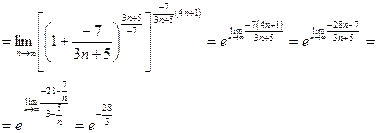
|
|
|
|
|
Дата добавления: 2014-11-07; Просмотров: 549; Нарушение авторских прав?; Мы поможем в написании вашей работы!