Задачи 11-20. Предварительно ознакомьтесь со следующими вопросами по теме «Кривые второго порядка»

Предварительно ознакомьтесь со следующими вопросами по теме «Кривые второго порядка»

1. Что называется кривой второго порядка?

2. Канонические уравнения кривых второго порядка. Графики этих кривых:

а) окружность:

б) эллипс: ;

в) гипербола: ;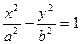

г) парабола: (с осью симметрии Оу),

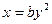(с осью симметрии Ох).

З. Параллельный перенос системы координат. Приведение уравнения второго порядка к каноническому виду.

Указанные виды кривых исчерпывают все виды кривых второго порядка (исключая случаи вырождения).

В результате решения задачи вы должны получить одну из названных кривых и построить ее в прямоугольной системе координат.

Задача. Составить уравнение линии, для каждой точки которой отношение расстояний до точки F(5;0) и до прямой 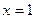равно .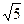

Решение. Построим в системе координат точку F(5;0) и вертикальную прямую Х=1(рис.2).

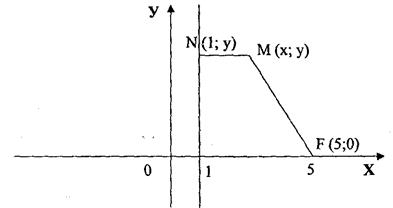
Рис.2.

Пусть М (х,у) - произвольная (текущая) точка искомой линии.

На рис. 2 изображены расстояния от этой точки до заданной точ­ки F, то есть MF, и до заданной прямой: х=1, то есть MN. Обратите внимание, что MN - перпендикуляр к заданной прямой и поэтому точ­ка N имеет (как и точка М) ординату, равную у: N(1;у).

По условию задачи

Выразим длины отрезков MF и MN через координаты их концов по формуле расстояния между точками:

;

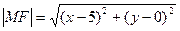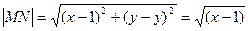
Тогда по условию

Это и есть уравнение искомой линии. Упростим его, возведя в квадрат обе части уравнения и сделав другие преобразования: ; ; ;

Разделим обе части уравнения на 20:

Это каноническое уравнение гиперболы. Из него видно, что дей­ствительная полуось гиперболы 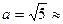2,25, мнимая полуось .

Центр симметрии гиперболы находится в начале координат. Для построения гиперболы отложим на осях координат в обе стороны от начала координат полуоси гиперболы 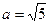и .

Через полученные точки «-а» и «а» на оси Ох и точки «-b» и «b» на оси Оу построим вспомогательный прямоугольник (рис. 3). Проведем диагонали этого прямоугольника, которые являются асим­птотами гиперболы: к ним будут неограниченно приближаться ветви гиперболы, Построим кривую, как указано на рис. 3. Задача решена.

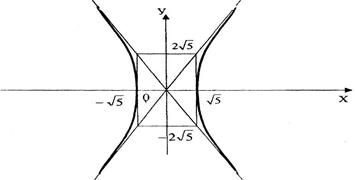
Рис. 3

Замечание. Если бы в этой задаче после преобразований вы получили уравнение

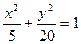
, то оно определяет эллипс, порядок построения которого ясен из рис.4.

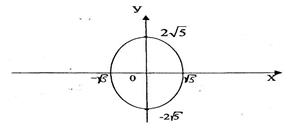
Рис.4

Замечание. Если в задаче вашего варианта после преобразований в уравнении наряду с членами и 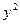присутствуют члены, содержа­щие первые степен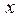и или , то следует выделить полный квадрат (соответственно по 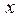или по ).

Например, в уравнении 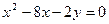выделим полный квадрат по 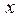, для чего прибавим и отнимем половину коэффициента при 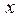, возве­денную в квадрат:

Обозначим 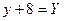; 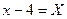, тогда 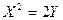или - это ка­ноническое уравнение параболы.

Построим новые оси и , которые смещены относительно старых осей и так, что новое начало координат будет нахо­диться в точке 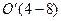, где и расположена вершина параболы. Ось симметрии параболы , ветви ее направлены вверх, так как коэф­фициент при 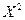положительный.

Полезно найти точки пересечения параболы 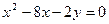со стары­ми осями координат и .

При получим , откуда , таким образом, пара­бола проходит через точку 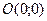- в старой системе координат.

При получаем уравнение 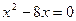, откуда т.е. пара­бола пересекает ось в точках 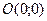и (8;0) (рис.5)

Рис.5

Дата добавления: 2014-11-07