Задачи 61-70

Найти полный дифференциал функции двух переменных

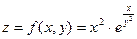
Решение. Полный дифференциал функции двух переменных на­ходим по формуле:

где ; 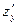--частные производные данной функции z.

Частные производные находим по обычным формулам дифферен­цирования для функции одной переменной, причем находим, счи­тая «у» постоянной величиной; аналогично при отыскании 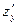счита­ем «х» постоянным:

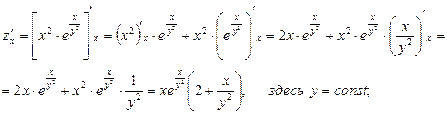
Отсюда полный дифференциал функции:

Задачи 71-80 и 81-90 относятся к теме «Интегральное исчисле­ние». Ознакомьтесь с основными вопросами этой темы:

1. Понятие первообразной и неопределенного интеграла.

2. Основные свойства неопределенного интеграла.

3. Таблица интегралов.

4. Основные методы интегрирования: непосредственное интегри­рование, интегрирование подстановкой, интегрирование по частям.

5. Интегрирование некоторых рациональных дробей.

6. Понятие определенного интеграла и его основные свойства.

7. Формула Ньютона-Лейбница для вычисления определенного интеграла.

8. Замена переменной и интегрирование по частям в определен­ном интеграле.

9. Применение определенного интеграла к вычислению площадей плоских фигур.

Интегрирование есть операция, обратная дифференцированию. ∫f(x)dx = F(x)+C, где F(х)-первообразная для подынтегральной функции f(x), то есть 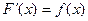, а С - произвольная постоянная. При интегрировании часто используют свойства неопределенного инте­грала:

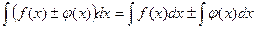
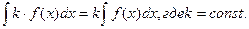
Идея интегрирования заключается в том, чтобы свести данный интеграл к одному из табличных интегралов. Поэтому, приступая к решению задач, ознакомьтесь с таблицей интегралов.

1.	1.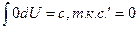
2.	2.
3.	3.
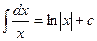
4.	4.
5.	5.
6.	6.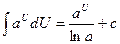
7.	7.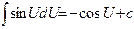
8.	8.
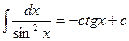
9.	9.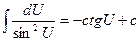
10.	10.
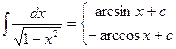
11.	11.
12.	12.
13.	13.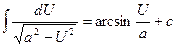
14.	14.
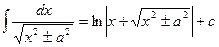
15.	15.
16.	16.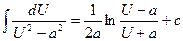

Примечание: Формулы интегрирования сохраняют свой вид при подстановке вместо независимой переменной любой дифференцируемой функции от нее, т.е. если

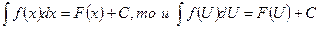
Tаким образом, применение основной таблицы сразу расширяется.

Например

Дата добавления: 2014-11-07