
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Задачи 11-20
|
|
|
|
Пример 14.
Пример 13.
Пример 12.
Пример 11.
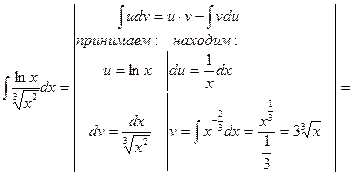
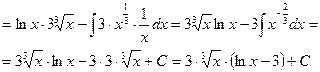


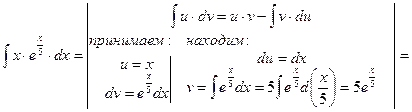

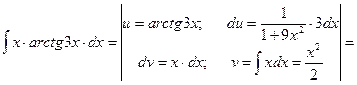
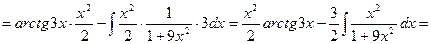
Чтобы взять последний интеграл, умножим и разделим числитель на 9, затем вчислителе прибавим иотнимем единицу, после чего разобьем интеграл на два табличных:
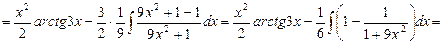
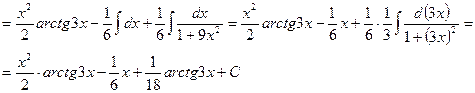 Обязательно сделайте проверку в примерах 6-14.
Обязательно сделайте проверку в примерах 6-14.
В этих задачах используется определенный интеграл, который вычисляется по формуле Ньютона-Лейбница.
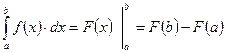
где F(x) - первообразная для f(x), то есть F'(x) = f(x);
a и b - пределы интегрирования, показывающие, как меняется переменная интегрирования х.
Обратите внимание на то, что определенный интеграл - это число в отличие от неопределенного интеграла, который является множеством функций. Формула Ньютона-Лейбница связывает определенный и неопределенный интегралы. Чтобы ею воспользоваться, следует взять сначала неопределенный интеграл (вернее, найти лишь одну первообразную, не прибавляя произвольной постоянной), а затем вычислить разность значений первообразной в верхнем и нижнем пределах интегрирования.
Например 
Задача. Вычислить площадь фигуры, ограниченной параболой 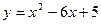 и прямой
и прямой 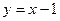 . Сделать чертеж.
. Сделать чертеж.
Решение. Построим параболу и прямую.
Для построения параболы найдем координаты ее вершины и точки пересечения ее с осями координат.
Вершина параболы является точкой экстремума, поэтому для ее отыскания найдем производную и приравняем ее к нулю.
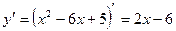 ;
; 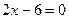 ;
; 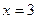 ,
,
Тогда  .
.
Итак, вершина параболы в точке 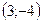 .
.
Точки пересечения параболы с осью Ох: 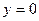 , тогда
, тогда
 , откуда
, откуда 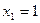 ;
; 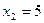 , то есть точки
, то есть точки 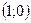 и
и 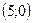 .
.
Точка пересечения с осью Оу: 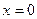 , тогда
, тогда  ; то есть точка
; то есть точка 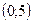 .
.
Строим параболу по найденным точкам, замечая, что ветви параболы направлены вверх (рис. 9).
Прямую у = х-1 строим по двум точкам: 
получены точки (0;-1) и (1;0). Заштрихуем плоскую фигуру, ограниченную параболой и прямой.

Найдем точки пересечения параболы и прямой, решив систему уравнений:
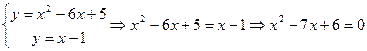
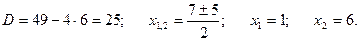
Для отыскания искомой площади воспользуемся формулой
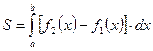 ,
,
где функции f1(x) и f2(x) ограничивают фигуру соответственно снизу и сверху, то есть f2(х) ≥f1 (х) при х Є [а;b].
В нашей задаче f1(x) = x2 -6x + 5;f2(x) = x-l; x Є [l;6].
Поэтому

Ответ: Площадь искомой криволинейной трапеции:
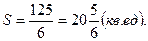
Тренировочные задания
1. Найти указанные пределы
1. 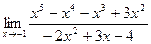 2.
2. 
3.  4.
4. 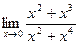
5. 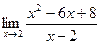 6.
6. 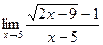
7. 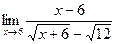 8.
8. 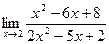
9.  10.
10. 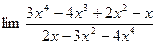
а) 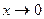 а)
а) 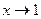
б) 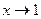 б)
б) 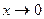
в) 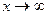 в)
в) 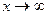
11. 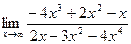 12.
12. 
13. 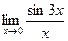 14.
14. 
15. 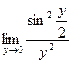 16.
16. 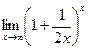
17. 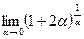 18.
18. 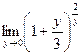
2. Найти производные и дифференциалы функции
1. 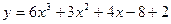 13.
13. 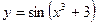
2. 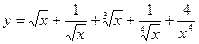 14.
14. 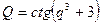
3. 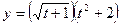 15.
15. 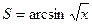
4. 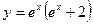 16.
16. 
5. 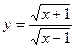 17.
17. 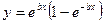
6. 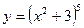 18.
18. 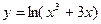
7. 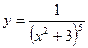 19.
19. 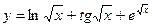
8. 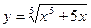 20.
20. 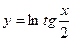
9. 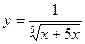 21.
21. 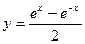
10. 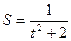 22.
22. 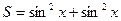
11. 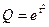 23.
23. 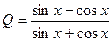
12.  24.
24. 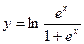
3. Найти полные дифференциалы для данных функций




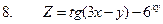
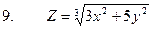
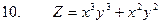
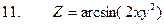
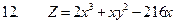
4. Найти неопределенные и определенные интегралы.
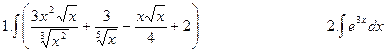







ПРАВИЛО ВЫБОРА ВАРИАНТА
Вариант контрольной работы определяется по таблице в зависимости от двух последних цифр номера шифра личного дела студента. В колонке таблицы по вертикали расположены цифры от 0 до 9, каждая из которых - предпоследняя цифра номера шифра. В верхней строке по горизонтали размещены так же цифры от 0 до 9, каждая из которых - последняя цифра шифра.
Пересечение вертикальной и горизонтальной линий определяет номера заданий контрольной работы. Например, по последним двум цифрам номера шифра «78» находят вариант контрольной работы на пересечении строки с цифрой 7 и столбца с цифрой 8. Для контрольной работы №1 это номера:5, 11, 27, 40, 41, 58, 70, 79, 82.
ТАБЛИЦА ВЫБОРА ВАРИАНТА КОНТРОЛЬНОЙ РАБОТЫ №1
| П р е д п о с л е д н я я Ц и ф р А ш и Ф Р а | Последняя цифра номера шифра | |||||||||
| Последняя цифра номера шифра | ||||||||||
| 73: | ||||||||||
| П р е д п о с л е д н я я Ц и ф р а ш и Ф р а | Последняя цифра номера шифра | |||||||||
|
|
|
|
|
Дата добавления: 2014-11-07; Просмотров: 375; Нарушение авторских прав?; Мы поможем в написании вашей работы!