Вимушені коливання. Резонанс

W0 t + j) - фаза коливання в момент часу t. Певні стану системи, що здійснює гармонічні коливання, повторюються через проміжок часу Т, що називається періодом коливання, за який фаза коливання чинить зріст рівне 2p, тобто

Коливаннями називаються руху або процеси, які характеризуються певною повторюваністю в часі. Коливальні процес широко поширені в природі і техніці, наприклад хитання маятника годин, змінний електричний струм і т.д. При коливальному рух маятника змінюється координата його центру мас, у випадку змінного струму коливаються напруга і струм в ланцюзі. Фізична природа коливань може бути різною тому розрізняють коливання механічні, електромагнітні та інші. Однак різні коливальні процеси описуються однаковими характеристиками і однаковими рівняннями. Звідси випливає доцільність єдиного підходу до вивчення коливань різної фізичної природи.

Гармонійні коливання та їх характеристики

Найпростішим типом коливань є гармонійні коливання - коливання, за яких коливається величина зміняться з часом зазаконом синуса (косінуса).
Гармонійні коливання величини s описуються рівнянням типу

s = A cos (w0 t + j), (1) де

А - максимальне значення коливається величини, що називається амплітудою коливання,

w0 - кругова (циклічна) частота,

j - початкова фаза коливання в момент часу t = 0,

w0 (t + T) + j = (w0t + j) 2 p, звідки T = 2p/w0
Гармонійні коливання зображуються графічно методом обертового вектора амплітуди, або методом векторних діаграм.
У теорії коливань приймається, що коливається величина s дорівнює дійсної частини комплексного виразу, що стоїть в цьому рівність справа.

3) диференціальне рівняння гармонічних коливань

D²/d*t²+w₀²_*x=0

4) Гармоні́чний осциля́тор — система (у класичній механіці), яка при зміщенні із положення рівноваги під дією певної сили (чи суперпозиції сил), повертається у попереднє положення під дією зворотної сили, пропорційної зміщенню (наприклад, за законом Гука у випадку механічних коливань):

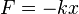
де 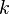— додатня константа, що описує жорсткість системи.

Якщо 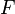— єдина сила, що діє на систему, то систему називають простим або консервативним гармонійним осцилятором. Вільні коливання такої системи є періодичний рух біля положення рівноваги (гармонійні коливання). Частота і амплітуда при цьому постійні, причому частота не залежить від амплітуди.
Якщо осцилятор існує сам по собі, то кажуть, що він робить вільні коливання. Якщо ж є зовнішня сила (що залежить від часу), то говорять, що осцилятор виконує вимушені коливання.

Також, можна дати еквівалентне означення гармонічному осцилятору — це фізичний об'єкт, еволюція якого з часом описується диференціальним рівнянням

,

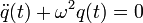де 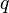— узагальнена координата гармонічного осцилятора, 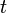— час, 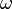— характерна частота гармонічного осцилятора. Дві крапки над змінною означають другу похідну за часом. Величина 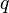здійснює гармонічні коливання.

Пружинный маятник — механическая система, состоящая из пружины с коэффициентом упругости (жёсткостью) k (закон Гука), один конец которой жёстко закреплён, а на втором находится груз массы m.

Когда на массивное тело действует упругая сила, возвращающая его в положение равновесия, оно совершает колебания около этого положения.Такое тело называют пружинным маятником

Фізи́чний ма́ятник — тверде тіло довільної форми, яке під дією сили тяжіння здійснює коливання навколо нерухомої горизонтальної осі, що не проходить через центр маси тіла.

Період коливань фізичного маятника визначається формулою

,

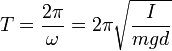де I - момент інерції, m - маса, d - віддаль від центра маси тіла до осі, g - прискорення вільного падіння.

Математи́чний ма́ятник — теоретична модель маятника, в якій матеріальна точка масою m підвішена на невагомій нерозтяжній і продовгуватій нитці та здійснює рух у вертикальній площині під впливом сили тяжіння.
Функція Лагранжа математичного маятника для узагальненої координати θ дорівнює

.

Рівняння Лагранжа

визначає рівняння руху маятника

.

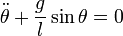5) Розглянемо перетворення енергії під час гармонічних коливань на прикладі пружинного маятника. Уважатимемо систему, що виконує вільні гармонічні коливання під дією пружної сили замкненою. У процесі коливання згідно із законом збереження енергії відбувається перетворення кінетичної енергії в потенціальну і, навпаки, але повна механічна енергія замкненої системи має залишатися незмінною.
З цією метою з'ясуємо, як змінюється в часі кінетична і потенціальна енергії. У формулу кінетичної енергії підставимо значення швидкості гармонічного коливання:.
Якщо в певну мить зміщення системи від положення рівноваги дорівнює х, то її потенціальна енергія дорівнює роботі пружної сили. Оскільки під час зміни зміщення від 0 до х величина пружної сили змінюється від F ₁ = 0 до F ₂ = kx
Таким чином, повна енергія системи, що виконує гармонічні коливання, пропорційна квадрату амплітуди коливань і не залежить від часу. Зі збільшенням кінетичної енергії системи зменшується її потенціальна енергія і, навпаки, але сума кінетичної і потенціальної енергій в довільний момент часу залишається сталою.

6)Биття
Биття́ — інтерференція двох звукових коливань, з частотами 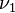і настільки близькими, що вони не сприймаються як два роздільні коливання. Амплітуда коливань, які виникають при цьому періодично збільшується чи зменшується у часі з частотою, рівною різниці інтерферуючих коливань

7) Фігури Ліссажу — замкнуті траєкторії, що прокреслюються точкою, що здійснює одночасно два гармонійних коливання у двох взаємно перпендикулярних напрямках. Вперше вивчені французьким ученим Ж. Ліссажу (фр. J. Lissajous; 1822-1880). Вид фігур залежить від співвідношення між періодами (частотами), фазами і амплітудами обох коливань. У найпростішому випадку (за рівності обох періодів) фігури являють собою еліпси, які при різниці фаз 0 або π вироджуються у відрізки прямих, а при різниці фаз π/2 і рівності амплітуд перетворюються в коло. Якщо періоди обох коливань не точно збігаються, то різниця фаз весь час змінюється, внаслідок чого еліпс весь час деформується. При істотно різних періодах фігури Ліссажу не спостерігаються. Однак, якщо періоди відносяться як цілі числа, то через проміжок часу, рівний найменшому кратному обох періодів, точка, що рухається, знову повертається в те ж положення — виходять фігури Ліссажу складнішої форми. Фігури Ліссажу вписуються в прямокутник, центр якого збігається з початком координат, а сторони паралельні осям координат і розташовані по обидва боки від них на відстанях, рівних амплітудами коливань.
Математичний вираз для кривої Ліссажу

8-9.Згасаючі коливання — коливання, енергія яких зменшується з плином часу.

Можуть бути 2х видів:

1.Однонаправні-движ.вдоль 1 оси;

2.взаимоперпендикулярні-движ.по оси х и перпендикулярной у.

Повна енергія тіла, що коливається, визначається амплітудою:

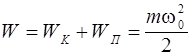. При зменшенні енергії амплітуда зменшується і коливання стає згасаючим.

Запишемо рівняння коливань у точці, що коливається в середовищі, коефіцієнт опорів якої r. По другому закону Ньютона

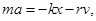
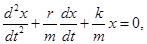
де β - коефіцієнт загасання. Цей коефіцієнт характеризує швидкість загасання коливань, При наявності сил опору енергія коливної системи буде поступово убувати, коливання будуть загасати.

-диференціальне рівняння загасаючих коливань.

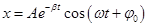
- рівняння загасаючих коливань.

ω –частота загасаючих коливань:

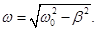
Період загасаючих коливань:

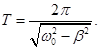
10.Характеристики згасання:

· час релаксації,

· кількість повних коливань за час релаксації.

· декремент згасання,

· логарифмічний декремент згасання,

· добротність коливальної системи,

Час релаксації - це час, за який амплітуда коливання зменшується в е разів

стала згасання визначає відносну зміну амплітуди коливань за одиницю часу –секунду.

Декремент згасання за визначенням є відношення амплітуд через період

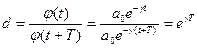
а логарифмічний декремент згасання за визначенням є

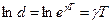
Добротність коливальної системи за визначенням є відношення її енергії в деякий момент часу до втрат енергії за проміжок часу, що дорівнює періоду коливань

Графік ідеалізованого власного коливання являє собою синусоїду або косинусоїду. Однак у будь-якій реальній коливальній системі, внаслідок неминучості дії сил тертя й опору, власні коливання згасають, тобто їх амплітуда зменшується з часом.

У природі і техніці дуже часто реалізуються не власні, а вимушені коливання, тобто коливання під дією зовнішньої (змушуючої) сили. Приклади: вимушені коливання здійснюють дерева і фрагменти споруд під натиском вітру; підлога машинного залу на заводі; міст під ногами людей, мембрана мікрофона та ін.

Вимушені коливання можуть бути незгасаючими, якщо зовнішня дія буде компенсувати зменшення енергії в системі, викликане дією сил тертя й опору.

Особливим проявом дії змушуючої сили є явище резонансу — стрімкого (різкого) зростання амплітуди вимушених коливань за умови збігу частоти власних коливань системи і частоти, з якою змінюється змушуюча сила.

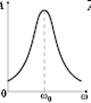
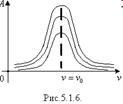
Графік залежності амплітуди коливань від частоти під час резонансу зображено на рис.5.1.6. Резонансна крива тим гостріша, чим менші втрати енергії в системі

Для послаблення шкідливої дії резонансу в техніці використовують гасителі коливань (демпфери), гумові та повстяні прокладки.

Під час коливань відбуваються взаємні періодичні перетворення потенціальної та кінетичної енергій.

.

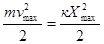Згідно із законом збереження енергії, кінетична енергія під час проходження системою положення рівноваги дорівнює її потенціальній енергії при максимальному відхиленні від цього положення.

12. Явление резкого возрастания амплитуды вынужденных колебаний при приближении частоты вынуждающей силы (частоты вынуждающего переменного напряжения) к частоте, равной или близкой собственной частоте колебательной системы, называется резонансом.

Чaстота́ — физическая величина, характеристика периодического процесса, равна количеству повторений или возникновения событий (процессов) в единицу времени. Рассчитывается, как отношение количества повторений или возникновения событий (процессов) к промежутку времени, за которое они совершены. Стандартные обозначения в формулах — ν, f или F. Частота обратно пропорциональна периоду колебаний: f = 1/ T.

Фаза колебаний — это величина, которая определяет положение колебательной системы в любой момент времени. Обозначается φ. Измеряется в радианах.
Если колебания происходят по закону синуса и косинуса, т. е. при гармонических колебаниях, то фаза колебаний является аргументом функции cos (ωt +φ_o),
где ω — циклическая частота колебаний,
t — время,
φ_o — начальная фаза колебаний, т. е. фаза в начальный момент времени.

13) Основними фізичними величинами, що характеризують коливальний контур (параметри контура), є його індуктивність, ємність та активний опір. Проте оскільки напруга є енергетичною характеристикою електричного поля, й енерпю електричного поля конденсатора визначають за формулою то зі зміною напруги відбуваються також періодичні зміни енергії електричного поля конденсатора (аналогічно змінам потенціальної енергії пружини у разі виникнення гармонічних коливань тягаря на пружині). На який же інший вид енергії перетворюється енергія електричного поля конденсатора? Під час перезарядження обкладок конденсатора в котушці виникає струм, сила якого визначає енергію магнітного поля:

Вимірювальні прилади покажуть, що коли напруга на обкладках конденсатора максимальна, то сила струму в колі дорівнює нулю, і навпаки, коли напруга дорівнює нулю, то сила струму максимальна. Отже, можна говорити про періодичні перетворення енергії електричного поля конденсатора на енергію магнітного поля котушки зі струмом і навпаки. Електричне коло, що складається з котушки і конденсатора, називають коливальним контуром, хоча, як побачимо, далі в таких колах не завжди можна спостерігати коливання. Досліджувані коливання швидко припиняються, що зумовлено витратами енергії на нагрівання провідників, перемагнічування феромагнітного осердя котушки, випромінювання частини енергії в простір у вигляді електромагнітних хвиль.

Енергія електричного поля конденсатора де С — ємність конденсатора, U — напруга на обкладках конденсатора, a q — заряд на одній з його обкладок.

Енергія магнітного поля котушки (провідника) 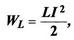де L — індуктивність котушки (провідника), I — сила струму в ній.

Лише в ідеальному випадку, коли б не було втрат енергії в коливальному контурі, максимальна енергія електричного поля конденсатора дорівнювала б максимальній енергії магнітного поля котушки зі струмом:

У цьому разі справджувався б закон збереження електромагнітної енергії, і в будь-який момент часу сума енергій електричного і магнітного полів залишалася б сталою:

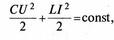деU і І — миттєві значення напруги і сили струму.

Ми бачили, що в коливальному контурі відбуваються коливання напруги, сили струму, заряду на обкладках конденсатора та інших електромагнітних величин (напруженості електричного поля, індукції магнітного поля тощо). Тепер потрібно встановити, якими параметрами коливального контуру визначаються період і частота коливань. Для цього можна поставити експеримент з використанням електронного осцилографа. Складемо електричне коло за схемою, наведеною на мал. 3.2. Ідеальним називають коливальний контур, у якому немає ніяких втрат електромагнітної енергії.

Отже, частота коливань — кількість коливань за одну секунду — дорівнює:

Період коливань: .

Дослідимо залежність частоти коливань від ємності конденсатора в коливальному контурі. Зафіксуємо три послідовні фази експерименту (мал. 3.4, а, б, в). На першому з них наведено графік коливань для ємності конденсатора 0,25, на другому — 0,5 і на третьому — 1,0 мкФ.
Індуктивність котушки контура та його активний опір при цьому залишаються сталими. За даними графіків пропонуємо встановити залежність частоти коливань від ємності конденсатора, після цього читати текст далі. У першому випадку протягом ¹ ₁₀₀с відбулося 10 повних коливань. Отже, частота коливань 1000 Гц. Коли ємність конденсатора збільшили вдвічі, частота коливань виявилося такою, що дорівнює 700 Гц, а коли ємність конденсатора збільшили ше вдвічі (у 4 рази порівняно з початковою), то частота зменшилася до 500 Гц. З цих результатів можна зробити висновок: зі збільшенням ємності конденсатора вдвічі, частота коливань зменшується у разів. Отже,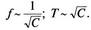

14) Електричний струм може бути постійним або змінним. Найбільшого поширення у світі дістав змінний струм частотою 50—60 Гц, створюваний індукційними генераторами. Однак для роботи багатьох пристроїв (комп’ютери, приймачі, телефони й ін.) необхідні змінні струми високих частот, вимірюваних кілогерцами (кГц) і мегагерцами (МГц). Для їх генерування застосовують спеціальні електричні кола — коливальні контури.

Будь-який коливальний контур складається з конденсатора й котушки індуктивності. Розглянемо його роботу на досліді. Для цього зберемо коло за схемою (рис. а). Спочатку конденсатор одержує енергію від джерела постійного струму. При цьому верхня пластина заряджається позитивно, а нижня негативно — на ній накопичується надлишок електронів. Перемкнімо конденсатор на котушку індуктивності (рис. б). Надлишок електронів з нижньої пластини конденсатора перекинеться через котушку до верхньої пластини, і в колі виникне наростаючий електричний струм. У результаті цього котушка стає електромагнітом і створює навколо себе магнітне поле.

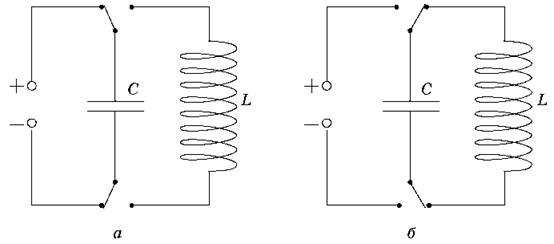
Через явище самоіндукції після розряджання конденсатора струм не припиниться миттєво, а буде продовжувати текти ще якийсь час у тому самому напрямку, знову заряджаючи пластини конденсатора. Після цього весь процес повториться в протилежному напрямку, і коливальний контур повернеться у вихідний стан.

Описаний процес перезарядження конденсатора через котушку повторюється через рівні проміжки часу. При цьому періодично змінюються значення електричного заряду конденсатора, напруги на ньому й сили струму в контурі.

Періодичні зміни електричного заряду, сили струму й напруги в колі називають електромагнітними коливаннями.

За відсутності втрат енергії в контурі електромагнітні коливання будуть гармонічними, тобто значення електричного заряду, сили струму й напруги в колі змінюватимуться за законом синуса або косинуса.

Англійський фізик Томсон вивів формулу для періоду електромагнітних коливань у контурі: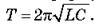

Використовуючи формулу Томсона, можна визначити власну частоту коливань коливального контуру:

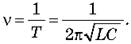
Заряджання конденсатора аналогічне відхиленню пружинного маятника від положення рівноваги, а енергія електричного поля зарядженого конденсатора — потенціальної енергії деформованої пружини.

Якщо конденсатор заряджений до напруги Um, то його заряд буде дорівнює qm = CUm. У цьому стані енергія електричного поля максимальна й дорівнює 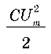. Цей стан еквівалентний стану пружинного маятника, коли пружину розтягли на х й передали механічній коливальній системі потенціальну енергію 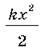. Коли конденсатор повністю розрядиться, енергія магнітного поля максимальна и дорівнює . Цей стан еквівалентний стану пружинного маятника, коли вантаж на пружині в положенні рівноваги має максимальну швидкість. Кінетична енергія маятника при цьому дорівнює 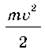. Коли сила струму зменшиться до нуля, конденсатор виявиться перезарядженим. Якщо втрат енергії в контурі немає, напруга й заряд конденсатора дорівнюватимуть початковим. Під час коливання вантажу на пружині цьому моменту відповідає його зупинка в крайньому верхньому положенні, коли потенціальна енергія максимальна.

Потім конденсатор почне знову розряджатися й у контурі виникне струм зворотного напрямку, енергія електричного поля зарядженого конденсатора буде зменшуватися, а магнітного — зростати. У певний момент часу конденсатор розрядиться, сила струму й енергія магнітного поля досягнуть максимальних значень. Це відповідає проходженню вантажем положення рівноваги.

Необхідно підкреслити ще раз, що максимальна енергія, накопичена в конденсаторі, під час коливань перетворюється в енергію магнітного поля котушки. Процес перетворення одного виду енергії в інший триватиме доти, доки в колі відбуватимуться коливання.

15) Змі́нний струм — електричний струм, сила якого періодично змінюється з часом.

Здебільшого коливання струму відбуваються за гармонічним законом

,

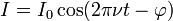де 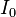— амплітуда струму, 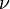— частота, 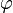— фаза струму.

Змінний струм виникає в електричному колі зі змінною напругою. Коливання напруги відбуваються за подібним законом, проте, в загальному випадку із зсувом фази

16) Векторная диаграмма - это изображение синусоидально изменяющихся величин в виде векторов на плоскости.

Векторные диаграммы применяют потому, что сложение и вычитание синусоидальных величин, неизбежные при расчете цепей переменного тока, наиболее просто выполняются в векторной форме. Кроме того векторные диаграммы отличаются простотой и наглядностью.

Построение векторной диаграммы выполняется в прямоугольной плоскости. Чтобы построить диаграмму нужно провести вектор длиною равный амплитудному значению искомой величины, под углом сдвига относительно другой величины. Возможно, вы не сразу поймете смысл сказанного, для этого нужно изучить пример.

В качестве примера рассмотрим построение векторной диаграммы для цепи, состоящей из последовательно подключенных конденсатора, резистора и катушки. Напряжение на катушке U_L=15 В, напряжение на конденсаторе U_C=20 В, напряжение на резисторе U_R=10 В, ток в цепи I=3 А. Требуется найти общее напряжение.

Катушка носит индуктивный характер, а значит, в ней напряжение опережает ток по фазе на 90°.

Конденсатор носит емкостной характер, значит, ток в нем опережает по фазе напряжение на 90°.

Резистор обладает только активным сопротивлением, и напряжение в нем совпадает по фазе с током.

Итак, для начала отложим вектор тока в масштабе. Масштаб для тока у нас будет 1 А/см.

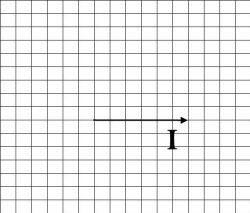
Теперь отложим вектор напряжения на катушке, масштаб для напряжения возьмем 5 В/см, получается, что нужно отложить шесть клеток вверх, так как напряжение в катушке опережает ток. Для наглядности обозначим синим цветом.

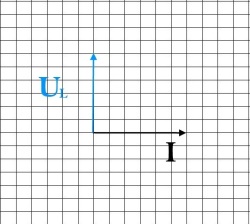
Далее мы будем откладывать вектор активного сопротивления, так как напряжение в одной фазе с током, то мы его откладываем из конца вектора U_Lпараллельно вектору тока I. Обозначим его красным цветом.

Следующим шагом отложим вектор напряжения на конденсаторе, так как оно запаздывает на 90°, мы его отложим вертикально вниз, из конца вектора U_R. Обозначим желтым цветом.

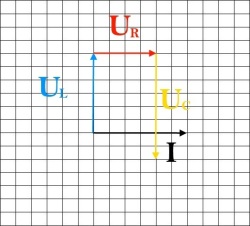
И последним этапом мы отложим вектор общего напряжения, из начала координат в конец вектора U_C и обозначим его зеленым цветом.

Общее напряжение получилось равным 2,23 В, причем характер цепи емкостной, так как напряжение отстает от тока.

Аналогичным образом выполняется построение векторной диаграммы токов

17) У випадку змінного струму закон Ома можна розширити, включивши в розгляд також елементи електричного кола, які характеризуються ємністю й індуктивністю. Змінний струм проходить через конденсатор, випереджаючи за фазою напругу. В індуктивності змінний струм відстає за фазою від напруги. Проте в обох випадках амплітуда змінного струму пропорційна амплітуді прикладеної змінної напруги. Математично це можна описати, ввівши комплексні опори (імпеданси).

Тоді можна записати

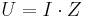
де U — амплітуда змінної напруги, I — амплітуда змінного струму, Z — імпеданс.

Імпеданс — комплексний опір.

Позначається здебільшого Z, вимірюється в Омах.

Імпеданс визначається, як

,

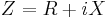де R — активний опір, X — реактивний опір

Дата добавления: 2014-11-07