Питання 23

Хвильове рівняння [ред. • ред. код]

Докладніше: Хвильове рівняння та Формула д'Аламбера

Рівняння (1), що описує розповсюдження збурень в струні, є частковим випадком загального рівняння в частинних похідних, яке називається хвильовим рівнянням. Для збурень в тривимірному середовищі хвильове рівняння в декартових координатах записується у вигляді:

(3)

Фізичний зміст введеної функції може бути різним залежно від фізичних властивостей середовища. Це може бути потенціал швидкостей точок середовища або збурення тиску. Рівняння такого типу належать до рівнянь гіперболічного типу і всебічно вивчаються математичною фізикою ^[4]. На першому малюнку показані поверхневі гравітаційні хвилі на воді. Характер руху в таких хвилях можна описати з допомогою потенціалу швидкостей 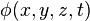. Однак, для такого типу збурень стисливістьводи виявляється несуттєвою ^[5].

За такої умови загальне хвильове рівняння зводиться до рівнянням Лапласа (права частина в (3) покладається рівною нулю).

Побудова розв'язків граничних задач із заданими початковими умовами для таких рівнянь у загальному випадку є досить складною проблемою. Однак, для одновимірного збурення, яке описується рівнянням (1), маємо унікальну ситуацію, коли вдається побудувати загальний розв'язок рівняння. Це рівняння було вперше отримано французьким математиком д'Ламбером 1747 року. Він же подав його загальний розв'язок у вигляді:

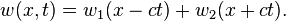
(4)

Тут 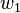і довільні двічі диференційовні функції від вказаних специфічних аргументів. Розв'язок д'Аламбера вказує на принципову особливість хвильового рівняння - сума будь-яких двох розв'язків є також розв'язком рівняння. Це частинній випадок принципу суперпозиції, що має місце для всіх лінійних задач математичної фізики. Для певної конкретної форми функції 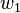зміна її в часі показана на рисунку. Видно, що ця функція описує розповсюдження збурення в струні в додатному напрямку осі . Другий доданок в рівнянні (4), очевидно, описує збурення, що розповсюджується в від'ємному напрямку осі . Таким чином, у загальному випадку будь які збурення в струні являють собою суму (суперпозицію) двох збурень, що розповсюджуються в протилежних напрямках. Конкретна форма збурень визначається початковими умовами.

До визначення фазової швидкості збурень в струні

На рисунку представлено зображення відрізку струни в два різні моменти часу. Видно, що збурення пересувається вправо без зміни форми зі швидкістю і саме цією швидкістю визначається відстань між точками, що перебувають в однаковій фазі відхилення від положення рівноваги. Саме цьому ця швидкість називається фазовою швидкістю хвилі. Графічна ілюстрація до визначення поняття фазової швидкості дозволяє звернути увагу на цікаву особливість хвильового руху в нескінченній струні. Як видно, точки струни, виведені з положення рівноваги зсувом у додатному напрямку вертикальної вісі, ніколи не перейдуть через положення рівноваги.

Дата добавления: 2014-11-07