Пример выполнения расчетно-графической работы №2. Задача К – 1.Определить абсолютную скорость и ускорение точки М

Задача К – 1. Определить абсолютную скорость и ускорение точки М.

Дано:

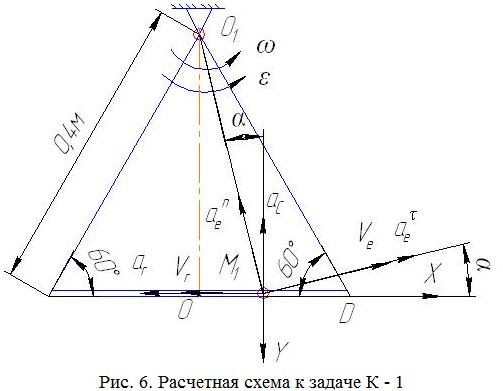
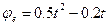; ; t=1c; а=0,4м; α=60°

Решение:

1. Свяжем неподвижную систему координат ОХ₁У₁ с пластиной. Тогда, движение точки М по прямой OD является относительным движением, а вращательное движение пластины – переносным.

2. При определении кинематических характеристик относительного движения мысленно останавливаем вращение пластины и рассматриваем только движении точки согласно заданному закону.

.

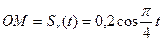В момент времен t₁=1c.

.

Так как S1>0, то точка М находится на стороне, показанной в расчетной схеме.

Найдем алгебраическую относительную скорость, и ускорение в произвольный момент времени

,

.

В момент времен t₁=1c.

,

.

Знаки показывают что вектор 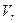и 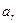направлены противоположно положительному отсчету S. Покажем эти векторы на чертеже.

3. При определении кинематических характеристик переносного движения, мысленно остановим точку М и рассмотрим только движение точки М₁ пластины. Тогда точка М₁ движется по окружности радиусом O₁М₁

.

Угловая скорость и угловое ускорение в произвольный момент времени равны:

,

.

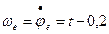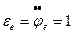В момент времен t₁=1c

,

.

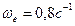Знаки указывают на то, что ускорение и скорость направлены согласно положительному направлению 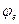, следовательно, против часовой стрелки.

Определим 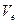и 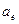в момент времен t1=1c:

,

,

.

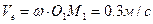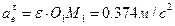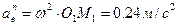Изобразим векторы на чертеже.

4. Модуль ускорения Кориолиса точки определим из выражения:

,

где 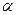- угол между вектором 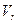и осью вращения. В момент времен t1=1c , откуда

.

Вектор 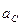перпендикулярен векторам 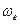и 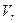, так что кратчайший поворот 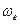до совмещения с вектором 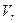, виден с конца вектора 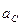против часовой стрелки.

5. Векторы и определяются по формулам:

,

.

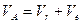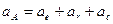Для определения векторов абсолютных скоростей и ускорений воспользуемся аналитическим методом, проведя координатные оси М₁ХУ.

Запишем равенство 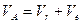в проекции на эти оси и определим абсолютную скорость.

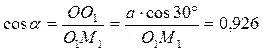, откуда ,

,

,

.

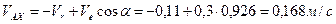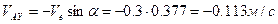Запишем теперь равенство в проекциях на оси координат и определим абсолютное ускорение в момент времени t1=1c:

,

,

.

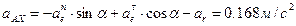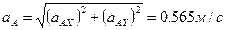Ответ: ; ; ; .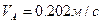

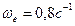Задача К – 2

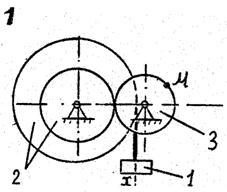
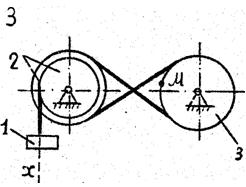
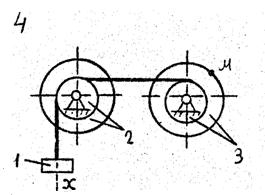
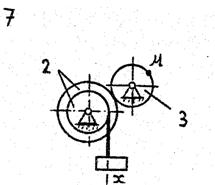
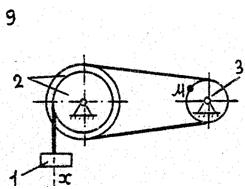
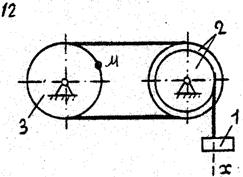
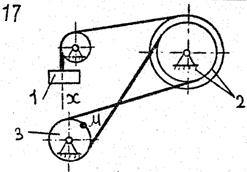
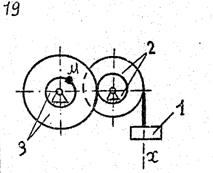
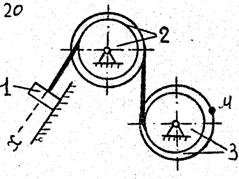
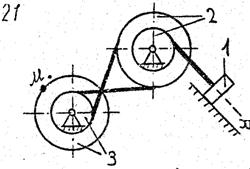
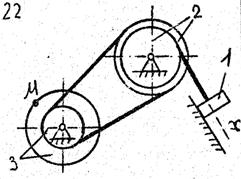
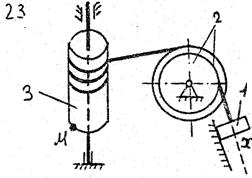
По данному уравнению прямолинейного поступательного движения груза 1 определить скорость, касательное, нормальное и полное ускорение точки М механизма в момент времени, когда путь, пройденный грузом, равен S.

VII. Данные к задаче К – 2

1 цифра шифра	R2, м	r2,м	R3,м	r3, м	2-я цифра шифра	x=x(t) (x, м; t, с)	S,м
	0,1	0,08	0,2	0,1		0,08+0,4	0,1
	0,2	0,16	0,3	0,25		0,05+0,6	0,2
	0,3	0,25	0,4	0,3		0,03+0,6	0,3
	0,4	0,3	0,3	0,15		0,03+0,4	0,6
	0,5	0,45	0,4	0,2		0,7	0,5
	0,6	0,5	0,5	0,4		0,03+0,3	0,4
	0,7	0,5	0,5	0,15		0,5	0,25
	0,6	0,4	0,4	0,25		0,02+0,5	0,3
	0,5	0,35	0,6	0.35		0,07+0,9	0,7
	0.4	0,25	0,5	0,45		0,03+0,7	0,2

Дата добавления: 2014-10-15