
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Электростатика. Данная тема изучает электростатическое поле, которое возникает при электриза-ции тел
|
|
|
|
1.2.1. Электрическое поле
Данная тема изучает электростатическое поле, которое возникает при электриза-ции тел. Сущность электризации состоит в том, что в теле создается тем или иным спо-собом избыток или недостаток электронов относительно количества положительных за-рядов этого тела. В электрически нейтральном теле число положительных зарядов в точности равно числу отрицательных зарядов.
Возникшее при электризации электрическое поле называется электростатическим, так как это поле связано с наэлектризованными неподвижными телами, т. е. оно не из-меняется относительно наблюдателя с течением времени.
1.2.2. Электронная теория строения вещества
Как известно, атом любого элемента состоит из ядра и электронной оболочки, ок-ружающей ядро. Ядро имеет положительный заряд, а электронная оболочка – отрица-тельный заряд, равный заряду ядра атома. Ядро атома состоит из протонов и нейтронов. Электрическая оболочка состоит из электронов, движущихся по определенным орбитам
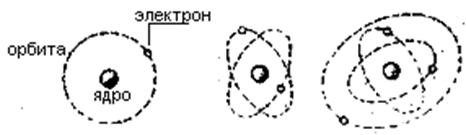 а б в Рис. 1.1. Модели атомов водорода (а), гелия (б), лития (в)
а б в Рис. 1.1. Модели атомов водорода (а), гелия (б), лития (в)
Электроны, образующие электронную оболочку ядра атома, вращаются вокруг яд-ра на различных уровнях. Самый устойчивым уровнем является тот, в котором всегда находятся восемь электронов. Элемент, у которого в наружном слое-уровне находятся восемь электронов, является химически нейтральным, т. е. он не вступает ни в какие хи-мические соединения с другими элементами.
Элементы, у атомов которых на наружном уровне (наружной орбите) меньше че-тырех электронов, сравнительно легко отдают эти электроны атомам других элементов. Элементы, у атомов которых на наружной орбите больше четырех электронов, стремят-ся дополнить этот наружный слой до восьми за счет атомов других элементов.
Атомы с избытком или недостатком электронов относительно числа положитель-ных зарядов (протонов) обладают уже иными свойствами и называются ионами.
Процесс электризации физических тел сводится к тому, что тем или иным способом создается избыток или недостаток электронов за счет изменения количества электронов наружного электронного слоя. Но в процессе этой электризации обязательно происходит преобразование определенного вида материи и расходуется связанная с ней энергия.
1.2.3. Закон Кулона
Известно, что наэлектризованные тела взаимодействуют друг с другом с опреде-ленной силой, не приходя в непосредственное соприкосновение.
Заряженные тела взаимодействуют друг с другом через электрические поля, кото-рые входят в непосредственное соприкосновение друг с другом. Ранее отмечалось, что при электризации тела и создании электрического заряда возникает электрическое поле, связанное с этим телом и этим зарядом. Величина электрического заряда тела может ха-рактеризовать электрическое поле, связанное с этим зарядом. В дальнейшем мы будем говорить о силе взаимодействия зарядов, что следует понимать как силу взаимодействия электрических полей заряженных тел.
Закон Кулона математически выражается формулой

|
|
|
|
где F – сила взаимодействия Н;
|
R – расстояние между зарядами, м;
ea – величина, называемая абсолютной диэлектрической проницаемостью, кото-
рая, в свою очередь, является произведением двух коэффициентов: eа= e0e, где e0– элек-трическая постоянная, имеющая размерность Ф/м, и определенной численной величины,

|
Величина e – диэлектрическая проницаемость. Данная величина, имея вполне оп-ределенный физический смысл, и определяет физический смысл 0.
С одной стороны, e определяется как величина, показывающая, во сколько раз уменьшится сила взаимодействия электрических зарядов в данной среде по сравнению
со взаимодействием в вакууме (это определение вытекает из формулы закона Кулона). С другой стороны, e – величина, характеризующая степень поляризации диэлектрика под действием электрического поля (об этом речь пойдет позже). Оба эти определения верны и отражают одну и ту же сущность явления. Предпочтительнее пользоваться вто-рым определением, так как на практике с этим приходится встречаться чаще всего.
1.2.4. Характерные свойства электростатического поля
Электростатическое поле создается при электризации физических тел. Оно всегда связано с наэлектризованными телами, электрическими зарядами. Центром электроста-тического поля является наэлектризованное тело, т. е. электрический заряд. Электроста-тическое поле распределено в пространстве, окружающем электрический заряд, и теоре-тически распространяется до бесконечности. Характерным признаком электро-статического поля является его действие с определенной механической силой как на не-подвижные, так и на движущиеся в этом поле электрические заряды. Только электриче-ское поле может действовать с определенной механической силой на неподвижные за-ряды. Только электрическое поле может привести в движение до этого неподвижные электрические заряды, находящиеся в проводнике. Электрическое поле, как и всякая ма-терия, обладает массой и энергией. Энергия электрического поля распределена во всем пространстве, занимаемом полем. Электрическое поле в каждой точке характеризуется напряженностью и потенциалом.
1.2.5. Напряженность электрического поля
Напряженность электрического поля – это силовая характеристика точки поля. На-пряженность поля характеризуется силой, с которой поле действует на электрический заряд, внесенный в данную точку поля. Напряженность электрического поля – векторная величина. За направление вектора напряженности электрического поля принимают на-правление силы, с которой поле действует на положительный заряд.
|
|

|
|
|
Для того чтобы можно было сравнивать напряженности различных точек иссле-дуемого поля, принято заряд Q 2брать равным единице. В этом случае сила F будет за-

|
|
|

|
силу, действующую на единицу заряда (на единичный заряд, равный одному кулону), найдем из соотношения



|
|
|
|
Данная величина является напряженностью электрического поля в данной точке и измеряется в В/м.
1.2.6. Линии электрического поля
Электрическое поле не действует ни на один из органов чувств, которые имеются у человека. Следовательно, человек не может непосредственно воспринимать электриче-ское поле. Это создает большие трудности при его изучении, так как все сказанное о форме и других особенностях поля можно только воображать, но нельзя видеть или ощущать его непосредственно. Чтобы как-то использовать для изучения электрического поля могучее оружие человека – зрение – введены линии электрического поля, которые позволяют изобразить картину электрического поля (рис. 2).
 Рис. 1.2. Примеры изображения электрического поля при помощи силовых линий:
Рис. 1.2. Примеры изображения электрического поля при помощи силовых линий:
а – электрическое поле одиночного положительного заряда; б – электрическое поле одиночного отрицательного заряда; в – электрическое поле двух разноименных зарядов; г – электрическое поле двух одноименных зарядов
Чтобы электрические силовые линии отображали картину электрического поля, их надо проводить по определенному закону. Этот закон заложен в самом определении си-ловых линий. Линии электрического поля – это линии, касательная к каждой точке кото-рых совпадает с вектором напряженности электрического поля.
|
1.2.7. Потенциал точки поля
Потенциал точки поля является энергетической характеристикой точки поля. По-тенциал характеризует потенциальную энергию точки поля. Как известно, мерой энер-гии, в том числе и потенциальной, является работа. Таким образом, по величине работы, совершаемой полем, мы можем судить об энергии поля.
Работа поля сводится к перемещению электрического заряда силами поля и равня-ется произведению силы на путь. Но сила зависит и от величины перемещаемого заряда. Значит, чтобы охарактеризовать электрические свойства в данной точке, необходимо всегда знать работу, совершаемую полем при перемещении единичного заряда, т. е. за-ряда, равного 1 К. Кроме того, вносимое заряженное тело должно быть достаточно ма-лых размеров, чтобы не исказить картину рассматриваемого поля.
Найдем, чему же равен путь, по которому должен перемещаться заряд из рассмат-риваемой точки поля, с тем чтобы определить всю потенциальную энергию данной точ-ки. Путь этот должен заканчиваться там, где кончается действие рассматриваемого поля, т. е. в бесконечности. Таким образом, мы пришли к определению потенциала. Потенци-ал точки поля численно равен работе, затрачиваемой полем на перемещение единичного заряда из данной точки в бесконечность или, наоборот, из бесконечности в данную точ-ку поля. Все зависит от знака поля и знака перемещаемого заряда.


|
|
|
|
2 дующим образом.
|

|
 1.2.8. Напряжение между двумя точками поля
1.2.8. Напряжение между двумя точками поля
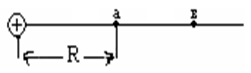
В электрическом поле, связанном с зарядом Q, рассмотрим две точки: а и б (рис. 1.3).
Обозначим потенциалы этих точек соответст-венно через f a и f б. Величины потенциалов этих точек можно выразить равенствами
а б
Рис. 1.3.


|
|
|
|
|

|
|
и будет равно потенциалу точки a и работе по перемещению единичного заряда от точ-

|
|
|
взяты так, что они лежат на одной силовой линии, и работу на перемещение заряда от точки a до бесконечности можно представить состоящей из двух слагаемых. Одно сла-
|
Следовательно, потенциал в точке a можно выразить так:


|
|
|
|
|
Из чертежа (рис. 1.3) и формул потенциалов точек a и б видно, что потенциал точ-ки a больше потенциала точки б. Найдем эту разность:



|
|
Иначе говоря, разность потенциалов точек a и б равна отношению энергии, затрачен-ной на перемещение заряда Q 2между этими точками, к величине заряда Q 2. Другими сло-вами, разность потенциалов между точками a и б равна работе, затраченной на перемеще-ние единичного заряда между точками, а это и есть напряжение между двумя точками:


|
|
|
Напряжение между двумя точками характеризует работу (энергию), затрачиваемую на перемещение единичного заряда между этими точками. Напряжение измеряется в вольтах, работа – в джоулях. Один вольт – это такое напряжение между двумя точками, когда между ними перемещается заряд в один кулон и при этом совершается работа в один джоуль.
1.2.9. Связь между напряжением и напряженностью электрического поля
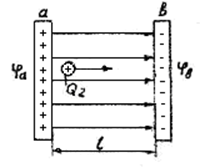 Этот вопрос удобнее рассмотреть для равномер-ного электрического поля. Поле называется равно-мерным, если напряженности всех его точек имеют одно и то же значение, а силовые линии параллель-ны друг другу. Такое поле образуется между двумя большими плоскостями, заряженными разноимен-ными зарядами (рис. 4).
Этот вопрос удобнее рассмотреть для равномер-ного электрического поля. Поле называется равно-мерным, если напряженности всех его точек имеют одно и то же значение, а силовые линии параллель-ны друг другу. Такое поле образуется между двумя большими плоскостями, заряженными разноимен-ными зарядами (рис. 4).
Работа на перемещение заряда Q 2 между ука-
занными плоскостями подсчитана так:
|
С другой стороны, эту же работу можно выразить следующей формулой:
|
или
|


|
|
т. е. напряженность электрического поля равна напряжению, приходящемуся на единицу длины. Теперь понятна и единица напряженности:


|
|
Проводниками называются тела, в которых имеются электрические заряды, спо-собные перемещаться под действием электрического поля. В твердых проводниках таки-ми зарядами являются свободные электроны (образующиеся за счет электронов наружных орбит атомов), которые слабо связаны с ядрами атомов и легко переходят от одного атома к другому. В жидкостях и газах перемещающимися зарядами являются ионы.
Представим себе электрическое поле уединенного положительного заряда (рис. 1.5). Поместим в это поле проводник, поперечное сечение которого (на том же рис. 1.5) изо-бражено в виде круга.
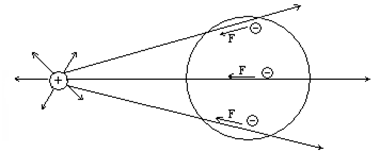 Рис. 1.5
Рис. 1.5
Свободные электроны проводника под действием сил электрического поля будут перемещаться к левой стороне проводника (рис. 1.5), а в правой стороне их окажется не-достаточно, вследствие чего положительные заряды там будут преобладать. Таким обра-зом, под действием электрического поля в проводнике произойдет разделение разноимен-ных зарядов. До каких пор будет продолжаться это разделение? Видимо, до тех пор, пока не перестанут действовать силы электрического поля на свободные электроны проводни-ка. И этот момент обязательно настанет, так как внутри проводника возникает свое элек-трическое поле, направленное навстречу внешнему электрическому полю. Картину элек-трического поля, образовавшегося внутри проводника, легко изобразить, если провести силовые линии между разделившимися зарядами проводника (рис. 1.6).
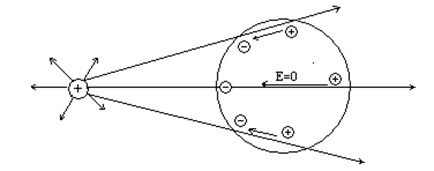 Рис. 1.6
Рис. 1.6
Когда поле, созданное внутри проводника, будет равно внешнему полю, тогда и прекратится разделение разноименных зарядов. Результирующее же поле внутри про-водника будет равно нулю. Таким образом, внутри проводника, находящегося в элек-трическом поле, электрическое поле равно нулю. Это явление используется для экрани-
рования деталей или устройств, которые надо защитить от воздействия внешних трических полей. В этом случае защищаемое устройство помещается внутри металличе-ского полого цилиндра или металлической сетки.
Электрическое поле под действием внесенного в него проводника изменит свою форму так, что силовые линии станут перпендикулярны поверхности проводника. В этом легко убедиться, если посмотреть на рис. 1.7, где взят один электрон, подошед-ший к левой поверхности и испытывающий действие силы F заряда Q. Разложим силу F на две силы: FN и F t. Составляющая сила FN стремится вырвать электрон с поверхности проводника. Под действием этой силы электрон двигаться не может. Составляющая сила F tперемещает электрон по поверхности проводника. Но по мере перемещения электрона по поверхности проводника сила F tбудет уменьшаться, а сила FN – расти. Электрон только тогда сделается неподвижным, когда сила F t с делается равной нулю.
 FN
FN
Рис. 1.7
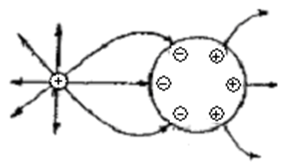 Таким образом, если проводник находится в электрическом поле и в проводнике не происходит перемещения электрических зарядов, то силы электрического поля направ-лены перпендикулярно поверхности проводника, т. е. под действием проводника меня-ется картина электрического поля.
Таким образом, если проводник находится в электрическом поле и в проводнике не происходит перемещения электрических зарядов, то силы электрического поля направ-лены перпендикулярно поверхности проводника, т. е. под действием проводника меня-ется картина электрического поля.
Рис. 1.8
В данном случае она будет иметь вид, изображенный на рис. 1.8, где проводник как бы разрывает электрические силовые линии внешнего электрического поля.
1.2.11. Диэлектрик в электрическом поле
Диэлектриками, или изоляторами, называют такие вещества, где нет свободных электрических зарядов, которые могут, двигаясь с места на место, покидать пределы своего атома, своей молекулы. Практически в каждом диэлектрике есть свободные элек-троны или ионы, но количество их ничтожно мало по сравнению с проводником. В це-лом ряде случаев мы не будем учитывать наличие в диэлектрике свободных электриче-ских зарядов.
Наименьшей частицей вещества, имеющего все его признаки, является молекула. Молекулы диэлектриков делятся на две группы: неполярные и полярные. У неполярных

|
|
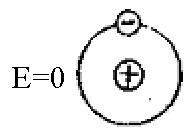
|
|
Рис. 1.9
Рис. 1.11
Рис. 1.10
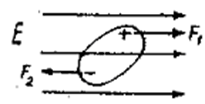 Рис. 1.12
Рис. 1.12
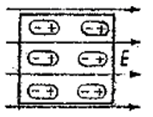
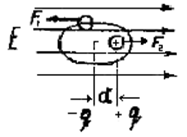
Диполи такого диэлектрика будут стремиться расположиться своими осями вдоль линий поля. Однако этому упорядочению расположения препятствует тепловое движе-ние. В результате произойдет лишь некоторый поворот диполей в направлении поля. Диэлектрик окажется поляризованным и степень его поляризации пропорциональна на-пряженности поля. В заключение можно сформулировать следующие выводы:
1. Под действием электрического поля диэлектрик поляризуется, т. е. становится полярным.
2. Под действием внешнего электрического поля в диэлектрике создается свое соб-ственное поле, направленное навстречу внешнему, но внутреннее поле диэлектрика все-
гда меньше внешнего. Результирующее поле в диэлектрике будет меньше внешнего поля в отличие от проводника, где внешнее поле полностью компенсируется внутренним по-лем и результирующее поле в проводнике равно нулю.
3. Степень поляризации диэлектрика характеризуется диэлектрической проницае-мостью e. Она показывает, во сколько раз ослабляется внешнее поле в диэлектрике под действием внутреннего поля. Теперь понятно, почему сила взаимодействия электриче-ских зарядов в диэлектрике меньше, чем в вакууме.
1.2.12. Токи смещения и проводимости
Если рассматривать конечный результат, то под действием электрического поля проводник и диэлектрик ведут себя как будто одинаково. Действительно, под действием внешнего поля и в проводнике, и в диэлектрике оказались с одной стороны положитель-ные заряды, а с другой – отрицательные. Но механизм образования этих зарядов в про-воднике и диэлектрике был совершенно различен. Действительно, в проводнике к одной его стороне подошли отрицательные заряды (электроны) из толщи самого проводника. При этом чем больше размер проводника, тем больше путь, пройденный электронами. Это было реальное направленное движение электрических зарядов, а такое движение и есть электрический ток.
Таким образом, ток, возникающий в результате направленного движения электри-ческих зарядов (электронов), называется током проводимости.
В диэлектрике также происходило перемещение электрических зарядов, но это пе-ремещение оставалось в пределах атома, молекулы. Заряд не покидал своего атома, свою молекулу. Происходило только некоторое смещение зарядов с прежнего их места при образовании диполя или перемещение зарядов при повороте диполя. Но это было на-правленное движение – это был электрический ток. Такой ток называется током смеще-ния. Он возникает в диэлектрике только в момент изменения электрического поля.
Если поле не изменяется, то ток смещения отсутствует. В свою очередь, ток прово-димости может существовать как в момент изменения поля, так и в том случае, если по-ле не изменяется.
Ток проводимости в диэлектрике при нормальных условиях мал, но он растет с ростом температуры диэлектрика, так как повышение температуры облегчает условия ионизации молекул.
При большой напряженности электрического поля происходит расщепление моле-кулы диэлектрика на ионы, а это уже обеспечивает в диэлектрике ток проводимости та-кой величины, что диэлектрик становится проводником. Напряженность электрического поля, при которой начинается ионизация молекул диэлектрика, называется пробивной напряженностью (электрической прочностью) диэлектрика.
1.2.13. Электрическая емкость
Под электроемкостью понимают способность тела сосредоточивать электрическое поле (электрические заряды).
Если взять металлический уединенный шар радиусом R, имеющий электрический заряд Q, то между величиной заряда Q и потенциалом поверхности шара существует
зависимость, выражаемая формулой

|
т. е. величина потенциала f поверхности шара прямо пропорциональна величине за-
ряда Q, находящегося на поверхности шара.

|
вой C и называется емкостью. Емкость шара C = 4pe0 R зависит только от геометриче-ских размеров шара и диэлектрической проницаемости диэлектрика, окружавшего шар. Речь идет о емкости уединенного тела.
 Рис. 1.13
Рис. 1.13

|
тать, что такой шар, как наша Земля, обладает емкостью меньше одной фарады. Доль-ными единицами емкости будет микрофарада (мкФ), равная 10−6Ф, и пикофарада (пФ), равная 10−12Ф. На емкость проводника оказывает влияние соседство других проводни-ков. Соседство других проводников увеличивает емкость данного проводника: чем бли-же проводники расположены друг к другу, тем больше будет емкость. Речь идет о емко-сти между проводниками. В этом случае емкость будет равна отношению величины заряда, расположенного на одном проводнике, к напряжению между проводниками:


|
|
Два провода, изолированные диэлектриком, называются конденсатором. Если про-водники выполнены в виде плоских пластин, то такой конденсатор называется плоским. Емкость плоского конденсатора рассчитывается по формуле

|
где S – площадь одной пластины, м2; d – расстояние между пластинами (толщина ди-электрика), м.
На рис. 1.13 показаны различные виды конденсаторов.
1.2.14. Параллельное соединение конденсаторов
Часто параметры одного конденсатора не удовлетворяют требованиям, предъяв-ляемым к нему в данной схеме (не подходит емкость или напряжение, на которое он рассчитан, или то и другое вместе). В этом случае приходится брать несколько конден-
саторов и соединять их так, чтобы группа этих конденсаторов (батарея) удовлетворяла требованиям, предъявленным к емкости в данной схеме. Конденсаторы соединяются между собой парал-лельно, последовательно или смешанно.
Конденсаторы будут соединены параллельно в том случае, если их обкладки с одной стороны подсоединены к одной общей точке, а обкладки с другой стороны – к другой общей точке (рис. 1.14). Батарея с параллельно соединенными конденсаторами об-ладает следующими свойствами:
1. Заряд батареи равен сумме зарядов, накопленных всеми конденсаторами, т. е.
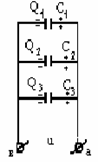 Рис. 1.14
Рис. 1.14
|
Действительно, величина заряда каждого конденсатора равна количеству электриче-ства, которое получил каждый конденсатор от источника. Заряд, израсходованный для этого источником, и будет зарядом батареи, равным количеству электричества, которое накоплено всеми конденсаторами.
2. Напряжения на параллельно соединенных конденсаторах равны между собой, так как эти напряжения равны разности потенциалов точек a и б:
U U 1 U 2= U 3.
3. Заряды на параллельно соединенных конденсаторах пропорциональны их емко-сти, так как


|
|
|
или
|
|
|


|
|
|
|


|
4. Общая емкость параллельно соединенных конденсаторов равна сумме емкостей всех конденсаторов. Поскольку
|
|
|
|
Так как все напряжения равны между собой, то будем иметь следующее соотноше-ние:
1.2.15. Последовательное соединение конденсаторов
Схема последовательного соединения конденсаторов представлена на рис. 1.15. Батарея с последовательно соединенными конденсаторами обладает следующими свой-
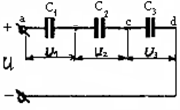 ствами:
ствами:
1. На конденсаторах будут одинаковые по величине б заряды, которые равны заряду всех батарей, поскольку
от источника энергии заряды поступают только на внеш-ние обкладки батареи, а на внутренних обкладках заряды возникают за счет разделения зарядов в соединительных
|
|
1 2 3
2. Общее напряжение батареи при последовательно соединенных конденсаторах равно сумме напряжений отдельных конденсаторов. Так как
U 1=fa−f в, U 2 в f c, U 3= c − d,
то
U 1 U 2+ U 3=fa f в + в f c + c f d f a f d.
Разность жe потенциалов точек а и d равна общему напряжению, т. е. U U 1+ U 2 U 3.
3. При последовательном соединении конденсаторов их напряжения обратно про-порциональны их емкостям. Поскольку
|
|
|


|
|




|
|
|




|
|
|
|
|








|
|
Для двух последовательно соединенных конденсаторов общую емкость целесооб-разно подсчитывать по формуле

|
|
|
Как правило, конденсаторы соединяются последовательно для уменьшения напря-жения, приходящегося на каждый конденсатор.
Если имеющиеся конденсаторы по емкости и напряжению не подходят для исполь-зования в той или иной схеме или устройстве, то их соединяют смешанно. Смешанное соединение конденсаторов есть сочетание последовательно и параллельно соединенных конденсаторов.
1.2.16. Расчет батарей при смешанном соединении конденсаторов
Когда требуется рассчитать батарею из смешанно-соединенных конденсаторов, то первая трудность, с которой встречаются студенты (курсанты), состоит в том, что они неверно представляют себе, когда, при каких условиях конденсаторы соединены парал-лельно и при каких – последовательно. Конденсаторы соединены последовательно толь-ко в том случае, когда к точке соединения двух конденсаторов больше ничего не при-соединено, т. е. эта точка не является точкой разветвления.
Конденсаторы соединены параллельно только в том случае, когда их обкладки с одной стороны присоединены к одной общей точке, а обкладки с другой стороны – к другой общей точке, т. е. обе эти точки являются точками разветвления.
Когда находится общая емкость двух или нескольких конденсаторов, то эту экви-валентную емкость целесообразно обозначать так, чтобы по самому обозначению было понятно, какие конденсаторы заменяют этот эквивалентный конденсатор. Например, на-до найти общую емкость третьего С 3и четвертого С 4конденсаторов. В этом случае их общую емкость целесообразно обозначить через С 3,4независимо от того, параллельно или последовательно они соединены. Аналогично эквивалентную емкость пяти конден-саторов, со второго по шестой включительно, можно обозначить через С 2–6. Нахождение общей емкости при смешанном соединении конденсаторов не вызывает больших труд-ностей, но нахождение напряжения на каждом конденсаторе дается не всем легко.
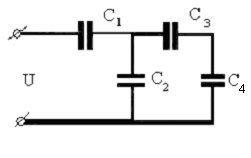 Каким образом это целесообразно делать, рассмотрим на следующем примере. Возьмем ба-тарею конденсаторов, изображенную на рис. 1.16.
Каким образом это целесообразно делать, рассмотрим на следующем примере. Возьмем ба-тарею конденсаторов, изображенную на рис. 1.16.
С 2= 5 мкФ, С 3= 4 мкФ, С 4= 12 мкФ, U = 1 200 В. Требуется найти напряжение на каждом конденсато-ре и величину заряда каждого конденсатора. Для того
чтобы приступить к расчету, надо разобраться, каким Рис.1.16 образом соединенымежду собойконденсаторы.
Из схемы (рис. 1.16) видно, что третий и четвертый конденсаторы соединены меж-ду собой последовательно. В этом случае их общая емкость C 3,4 находится по формуле


|
|