
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Переменный ток
|
|
|
|
2.1.1. Общие понятия и определения
 Переменный ток – это ток, изменяющийся с тече-нием времени по величине и направлению.
Переменный ток – это ток, изменяющийся с тече-нием времени по величине и направлению.
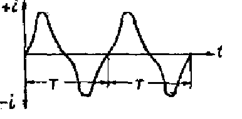
В общем случае переменный ток – сложный ток, изменения которого не подчиняются какой-либо зако-номерности (рис. 2.1).
На практике чаще всего приходится иметь дело с периодическим током. Периодический ток – это пере-
менный ток, изменения которого повторяются периоди- Рис.2.1
чески через равные промежутки времени, называемые периодом. Период обозначается буквой Т (рис. 2.2).
Периодический ток вообще – ток сложной формы. Его изменения могут быть са-мыми различными, но у него уже есть определенная закономерность изменения: в каж-дый новый период он изменяется точно так же, как и в предыдущий.
 В технике обычно имеют дело с самым про-стым периодическим током – синусоидальным, изменения которого совершаются по закону си-нуса. Под термином «переменный ток» понимают ток синусоидальный.
В технике обычно имеют дело с самым про-стым периодическим током – синусоидальным, изменения которого совершаются по закону си-нуса. Под термином «переменный ток» понимают ток синусоидальный.
Все токи, изменяющиеся по любому друго-му закону (несинусоидальному), называют неси-
Рис.2.2 нусоидальными токами.
|
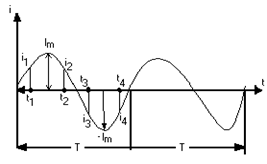 значение синусоидальной величины называет-ся амплитудой. Амплитуды тока, напряжения и ЭДС обозначаются большими буквами с ин-дексом m (Im, Um, Em).
значение синусоидальной величины называет-ся амплитудой. Амплитуды тока, напряжения и ЭДС обозначаются большими буквами с ин-дексом m (Im, Um, Em).
Период – это отрезок времени, по исте-чении которого изменения периодических ве-личин повторяются. Период измеряется в се-кундах (с). Число периодов за 1 с называется частотой, обозначается буквой f и измеряется

|
При вращении проводника в равномерном магнитном поле с постоянной угловой скоростью w в проводнике индуктируется синусоидальная ЭДС e = Em sinw t.
Если магнитное поле двухполюсное, то время одного оборота рамки равно периоду Т. Если генератор имеет p пар полюсов, то за один оборот совершается p периодов.
Уравнение ЭДС (тока или напряжения) может иметь и другой вид. Все зависит от того, как выражать угловую скорость w. Для двухполюсного генератора угловую ско-рость можно определить так:


|
|
 тогда уравнения синусоидальной ЭДС или другой величины будут иметь следующий вид: e = Em sinw t, e = Em sin 2p t, e = Em sin2p ft.
тогда уравнения синусоидальной ЭДС или другой величины будут иметь следующий вид: e = Em sinw t, e = Em sin 2p t, e = Em sin2p ft.
Если вращать в магнитном поле не одну, а несколько рамок, жестко скрепленных между собою под некоторыми углами 1, 2, a3, то ЭДС, индуктируемые в рамках, бу-дут отличаться друг от друга только тем, что они будут достигать одноименных значе-ний (одинаковых по названию) не одновременно, а в различные моменты времени. В этом случае говорят, что синусоидальные величины не совпадают по фазе – между
 ними есть сдвиг фаз. Такие синусоидальные чины в начальный момент времени (t 0) будут иметь разные значения.
ними есть сдвиг фаз. Такие синусоидальные чины в начальный момент времени (t 0) будут иметь разные значения.
|
Угол, определяющий значения синусоидальной величины в начальный момент времени, называется начальной фазой.
Уравнения синусоидальных величин, сдвинутых по фазе, имеют следующий вид:
В этих уравнениях углы y1, y2, y3являются начальными фазами. Угол сдвига фаз равен разности начальных фаз:
y12 = y1 −y2, 13 1 − 3, 23 = 2 − 3.
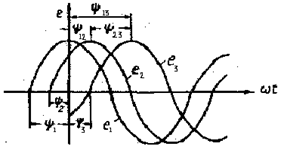 Угол, определяющий значение синусоидальной величины в данный момент времени, называется фазой. В приведенных выше уравнениях для первой ЭДС (е 1) фазой является угол w t +y1, для второй ЭДС (е 2) – угол
Угол, определяющий значение синусоидальной величины в данный момент времени, называется фазой. В приведенных выше уравнениях для первой ЭДС (е 1) фазой является угол w t +y1, для второй ЭДС (е 2) – угол
w t +y2, для третьей ЭДС (е 3) – угол w t + 3.
На рис. 2.4 приведены графики синусои-дальных величин, сдвинутых по фазе, отмече-ны углы начальных фаз и углы сдвига фаз.
Любая периодическая величина полно-стью может быть охарактеризована некото-рыми постоянными величинами, которые в
этом случае называются ее параметрами. Так, Рис.2.4 параметрами синусоидальных величин (тока,
напряжения, ЭДС и др.) являются амплитуда, период или частота, начальная фаза или сдвиг фаз. Если мы знаем параметры синусоидальной величины, то мы знаем о ней все.
2.1.2. Векторное изображение синусоидальных величин
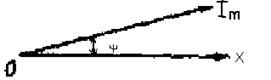
В основу векторного изображения синусоидальных величин положено следующее: при вращении вектора длиною, равной амплитудному значению синусоидальной вели-чины, против часовой стрелки со скоростью проекция вектора на вертикальную ось изменяется по закону синуса, т. е. по тому же закону, по какому изменяется мгновенное значение синусоидальной величины. Для векторного изображения синусоидальной ве-личины вектор, равный ее амплитудному значению, откладывают к горизонтальной оси под углом, равным начальной фазе.
Ток, представленный уравнением i = Im sin(t +), векторно изображается так, как это показано на рис. 2.5.
На рис. 2.6, б, в показано, как векторно находить сумму двух синусоидных вели-чин, представленных векторами (рис. 2.6, а), применяя правило параллелограмма и тре-угольника (многоугольника).
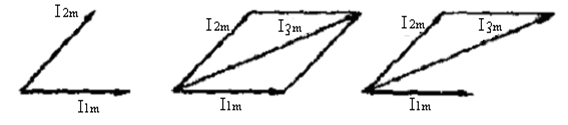 а б в Рис. 2.6
а б в Рис. 2.6
На рис. 2.7, б, в, г показаны три способа нахождения разности синусоидальных ве-личин, представленных векторно на рис. 2.7, а.
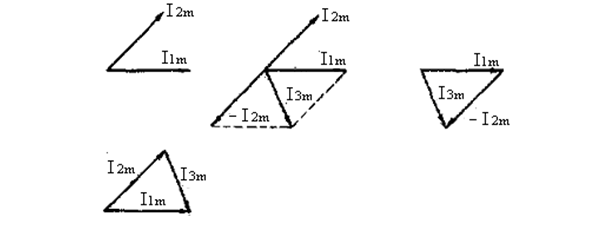 а
а
б в
г
Рис. 2.7
Эффективность действия переменного тока оценивается так называемым дейст-вующим, или эффективным, его значением.
Действующее значение переменного тока равно такому значению постоянного тока, которое вызывает такой же тепловой эффект, как и рассматриваемый переменный ток.
Для синусоидальных величин действующее значение равно амплитудному значе-
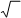 нию, деленному на 2.
нию, деленному на 2.
Действующие значения тока, напряжения, ЭДС обозначаются такими же буквами, как и для постоянного тока:
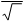
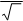
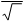
|
2.1.3. Электрическое сопротивление
Сопротивление понимается как некоторое препятствие прохождению электрическо-го тока. Эти препятствия могут иметь различную физическую сущность, а следовательно, и характер сопротивления бывает различным. Однако каким бы ни был характер сопро-тивления, на нем всегда теряется часть напряжения источника, что и является признаком наличия сопротивления на данном участке цепи. Из этого следует, что если на участке це-пи теряется часть напряжения источника, то этот участок обладает сопротивлением.
Напряжение на участке цепи может теряться по разным причинам. Одна из них со-стоит в том, что на участке цепи электрическая энергия преобразуется в другую форму энергии (тепловую, световую и т. д.). В данном случае говорят, что этот участок облада-ет активным сопротивлением. Для постоянного тока сопротивление определяется нали-чием физических носителей тока – электрических зарядов, способных перемещаться под
действием сил электрического поля. Если носителей тока (свободных электронов в твер-дых телах, ионов в жидкостях и газах) в единице объема данного вещества много, то те-ло обладает небольшим сопротивлением. Если же этих носителей тока мало, то тело об-ладает большим сопротивлением (при прочих равных условиях), так как во втором случае ток будет меньше, чем в первом.
Активное сопротивление проводника переменному току больше сопротивления по-стоянному току из-за явления поверхностного эффекта – оттеснения тока из центра про-водника к его поверхности. Благодаря этому уменьшается площадь поперечного сечения проводника для переменного тока по сравнению с постоянным током.
Практически активное сопротивление подсчитывается по формуле

|
 где – мощность, потребляемая на данном участке цепи; I – действующее значение переменного тока.
где – мощность, потребляемая на данном участке цепи; I – действующее значение переменного тока.
Активное сопротивление обозначается буквой R, а на чертеже знаком.
2.1.4. Индуктивное сопротивление
Если на участке цепи теряется часть напряжения источника на уравновешивание ЭДС самоиндукции, то говорят, что этот участок обладает индуктивным сопротивлением.
Электродвижущая сила самоиндукции согласно правилу Ленца противодействует всякому изменению тока. Если по цепи течет переменный ток, то причиной возникнове-ния ЭДС самоиндукции является именно изменение тока. ЭДС самоиндукции препятст-вует прохождению переменного тока, а внешне мы воспринимаем это как наличие неко-торого сопротивления в данной цепи.
Конечно, не надо отождествлять величину ЭДС с величиной индуктивного сопротив-ления, но несомненно, что это сопротивление и ЭДС прямо пропорциональны, так как ЭДС прямо пропорциональна произведению величины тока и индуктивного сопротивления. Ин-дуктивное же сопротивление для линейных элементов не зависит от величины тока.
 Индуктивное сопротивление обозначается буквой XL, а на чертеже знаком.
Индуктивное сопротивление обозначается буквой XL, а на чертеже знаком.
2.1.5. Емкостное сопротивление
Емкость влияет также на величину тока в цепи, следовательно, она проявляет себя как некоторое сопротивление. Для постоянного тока (рассматриваем только установив-шийся процесс) емкость обладает бесконечно большим сопротивлением. Это означает разрыв в цепи, так как тока в такой цепи не будет.
Емкость, включенная в цепь переменного тока, уменьшает величину тока (рас-сматриваем случай, когда в цепи нет индуктивности). Когда напряжение сети растет, то конденсатор заряжается, накапливаемые заряды на обкладках конденсатора противодей-ствуют вновь подходящим зарядам (одноименные заряды отталкиваются) и ток в цепи уменьшается. При уменьшении напряжения источника конденсатор разряжается – и этим поддерживает ток в цепи. Следовательно, конденсатор противодействует измене-нию тока, т. е. он противодействует прохождению переменного тока, а это мы и воспри-нимаем как определенное сопротивление. Сопротивление конденсатора называется ем-костным сопротивлением и обозначается буквой Xc, а на схеме знаком --||--.
2.1.6. Цепь переменного тока только с активным сопротивлением
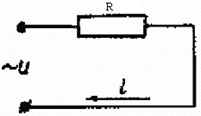 В данной цепи отсутствуют индуктивность и емкость, а имеется только активное сопротивление, преобразующее электрическую энергию в другой вид энергии (рис. 2.8).
В данной цепи отсутствуют индуктивность и емкость, а имеется только активное сопротивление, преобразующее электрическую энергию в другой вид энергии (рис. 2.8).
При напряжении источника u = Um sin t ток в


|
|
|

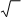
|
|

|
т. е. для этой цепи и действующих значений тока и напряжения формула закона Ома имеет такой же вид, как и для постоянного тока.
Мгновеннаямощностьвцепитолькосактивнымсопротивлениемвсегдаположительна:
|
|
|
|



|
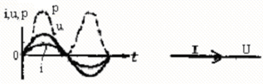 На рис. 2.9 показаны графики напряже-ния, тока и мощности этой цепи, а также век-торная диаграмма тока и напряжения.
На рис. 2.9 показаны графики напряже-ния, тока и мощности этой цепи, а также век-торная диаграмма тока и напряжения.
Рис. 2.9
2.1.7. Цепь переменного тока только с индуктивностью
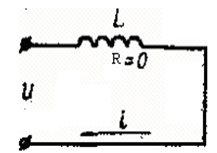 При прохождении по такой цепи тока i = Im sinw t (рис. 2.10) в цепи возникает ЭДС са-
При прохождении по такой цепи тока i = Im sinw t (рис. 2.10) в цепи возникает ЭДС са-

|
скорости изменения тока. ~ При синусоидальном изменении тока (рис.
2.11) наибольшая скорость его будет в момент прохождения тока через нулевые значения, и ЭДС
в эти моменты будет наибольшая. При наиболь- Рис. 2.10
шем значении тока Im скорость его изменения равна нулю, и ЭДС в эти моменты време-
ни тоже будет равна нулю. Согласно правилу Ленца ЭДС самоиндукции препятствует всякому изменению тока, благодаря чему в моменты нарастания тока она всегда дейст-вует навстречу току (ток и ЭДС будут иметь разные знаки). В моменты убывания тока ЭДС действует в том же направлении, что и ток (ток и ЭДС будут иметь одинаковые знаки). Согласно второму закону Кирхгофа для рассматриваемой цепи будем иметь
u eL iR = 0.
Тогда

|
Поскольку
i Im sinw t, то

|
При cosw t =1 напряжение будет максимальным, т. е. u Um Im w L, и значение напряжения в любой момент времени можно записать так:

Другими словами, в чисто индуктивной цепи напряжение опережает ток на чет-верть периода, а ЭДС будет противоположна по фазе напряжению и будет отставать по фазе от тока на четверть периода. Так как
Um = Im L,
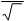
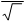
|
то


|
при этом величина XL = w L = 2p fL называется индуктивным сопротивлением.
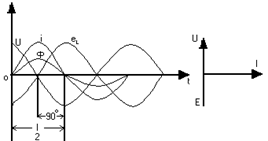 Рис. 2.11
Рис. 2.11
|
На рис. 2.11 приведены графики тока, магнитного потока, ЭДС самоиндукции, на-пряжения, а также изображена векторная диаграмма тока, ЭДС и напряжения чисто ин-дуктивной цепи.
Указанные графики иллюстрируют изложенный выше физический процесс, проис-ходящий в данной цепи.
2.1.8. Мгновенная мощность в цепи только с индуктивностью

Она изменяется по закону синуса с удвоенной частотой по сравнению с частотой тока и напряжения (рис. 2.12).
Из уравнения мощности p = UI sin2w t видно,

|
Рис. 2.12
ò pdt ò UI sin2w t



|
|
Другими словами, в этой цепи нет расхода энергии, а есть только обмен энергией между источником и потребителем.
На рис. 2.12 приведены графики напряжения, тока и мощности чисто индуктив-ной цепи.
2.1.9. Последовательное соединение активного сопротивления и индуктивности
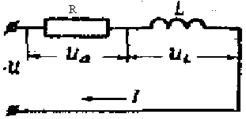 При последовательном соединении ток во всех участках цепи один и тот же и равен I А (рис. 2.13).
При последовательном соединении ток во всех участках цепи один и тот же и равен I А (рис. 2.13).
Напряжение, теряемое на активном со-противлении, совпадает по фазе с током и рав-
но UR. Это напряжение называется активным падением напряжения U.
Напряжение на индуктивном сопротивле-
Рис. 2.13
нии будем обозначать как UL. Оно опережает по фазе ток на четверть периода и равно IXL. Общее напряжение при последовательном соединении равно сумме напряжений на
отдельных участках. Поскольку расчет ведется для действующих значений, то эта сумма будет геометрической, т. е. напряжения надо складывать векторно (рис. 2.14). Получен-ный треугольник называется треугольником напряжений. Из него видно, что при последо-вательном соединении активного сопротивления и индуктивности общее напряжение опе-режает ток на угол. В этой цепи активное падение напряжения, индуктивное падение
напряжения и общее напряжение связаны как стороны прямоугольного треугольника, т.
|
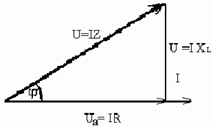 е.
е.



|
|
откуда
I =
U
R 2 + X 2

|


|
|
|
выражает закон Ома для данной цепи.
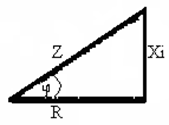 Если каждую сторону треугольника напряжений раз-делить на ток, то получится треугольник сопротивлений, подобный треугольнику напряжений (рис. 2.15). Из тре-угольника сопротивлений следует:
Если каждую сторону треугольника напряжений раз-делить на ток, то получится треугольник сопротивлений, подобный треугольнику напряжений (рис. 2.15). Из тре-угольника сопротивлений следует:


|
|



|
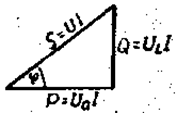 т. е. активное, индуктивное и полное сопротивления связаны между собой как стороны прямоугольного треугольника. Если каждую сторону треугольника напряжений умножить на ток (а треугольник сопротивлений на квадрат тока), то получится треугольник мощно-стей (рис. 2.16), где P = UaI = I 2 R = S cosf = UI cosf – активная мощность, которая пока-зывает количество электрической энергии, ежесекундно
т. е. активное, индуктивное и полное сопротивления связаны между собой как стороны прямоугольного треугольника. Если каждую сторону треугольника напряжений умножить на ток (а треугольник сопротивлений на квадрат тока), то получится треугольник мощно-стей (рис. 2.16), где P = UaI = I 2 R = S cosf = UI cosf – активная мощность, которая пока-зывает количество электрической энергии, ежесекундно
преобразуемой в другой вид энергии, Вт; S = UI = I 2 z – полная, или кажущаяся, мощность, которая показывает ко-личество электрической энергии, ежесекундно доставляе-
мой электромагнитным полем потребителю. Измеряется она в вольт-амперах (ВА). Множитель cosf называется коэф-
фициентом мощности и характеризует степень использова- Рис.2.16 ния энергии электромагнитного поля потребителем:



|
|
Величина Q = ULI = I 2 XL = S sinf = UI sinf – реактивная мощность, измеряемая в вольт-амперах реактивных (ВАр). Она характеризует скорость обмена энергией между источником и потребителем.
2.1.10. Последовательное соединение нескольких разнородных сопротивлений
Пусть будут соединены последовательно две катушки индуктивности, каждая из которых обладает как активным, так и индуктивным сопротивлением (рис. 2.17). Ток во всех участках цепи одни и тот же.
|

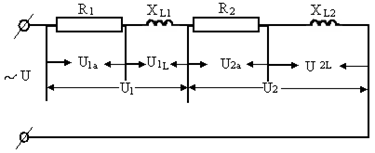 Рис. 2.17
Рис. 2.17
При его прохождении на всех участках цепи создаются падения напряжения, кото-рые соответственно определяются по формулам
причем активные падения напряжения Ua 1 и Ua 2 совпадают по фазе с током, а индук-тивные напряжения UL 1 и UL 2 опережают ток по фазе на четверть периода.
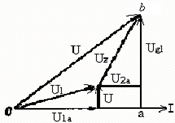 Чтобы найти общее напряжение, сложим векторно все напряжения в такой же последовательности, как это изображено на схеме (рис. 2.17). В результате получим векторную диаграмму, изображенную на рис. 2.18, из ко-торой следует:
Чтобы найти общее напряжение, сложим векторно все напряжения в такой же последовательности, как это изображено на схеме (рис. 2.17). В результате получим векторную диаграмму, изображенную на рис. 2.18, из ко-торой следует:
 oв = (oa)2 +(aв)2,
oв = (oa)2 +(aв)2,
где oв = U, oa = Ua 1 + Ua 2, aв = UL 1 + UL 2. Рис.2.18 Следовательно,
 U = (Ua 1+ Ua 2)2+(UL 1+ UL 2)2.
U = (Ua 1+ Ua 2)2+(UL 1+ UL 2)2.
Так как
|


|
Решение этого уравнения относительно тока дает формулу закона Ома для этой цепи
I =
U

|
= U.
Обобщая последнее выражение для какого угодно числа разнородных сопротивле-ний, можно записать:
 z =(R)2+(å XL)2.
z =(R)2+(å XL)2.
Иначе говоря, общее сопротивление при последовательном соединении разнород-ных сопротивлений равно квадратному корню из квадрата суммы активных сопротивле-ний плюс квадрат суммы индуктивных (реактивных) сопротивлений.
2.1.11. Цепь переменного тока только с емкостью
В данной цепи отсутствуют активное сопротивление и индуктивность – имеется толь-ко емкость (рис. 2.19).



|
|
|
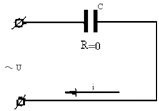 При напряжении u Um sinw t, приложенном к цепи, ток, определяемый по формуле
При напряжении u Um sinw t, приложенном к цепи, ток, определяемый по формуле
dq Cdu CdUm sin
dt dt dt
t = CUm wcosw t,
будет опережать по фазе напряжение на четверть периода. Рис.2.19 При cosw t =1 ток будет наибольшим:
i = Im Um C.
Тогда значение тока в любой момент времени можно записать как
 i = Im cosw t = Im sin(w t + 2),
i = Im cosw t = Im sin(w t + 2),
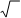
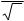
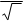
|
или


|
 w C C
w C C
 где последние равенства выражают закон Ома для чисто ем-
где последние равенства выражают закон Ома для чисто ем-
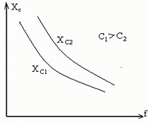
костной цепи. Выражение
1 1

 w C 2p fC
w C 2p fC
имеет размерность со-
противления и называется емкостным сопротивлением. Оно обратно пропорционально частоте и емкости, что графически представлено на рис. 2.20.
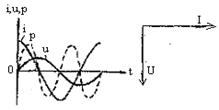
Мгновенная мощность в чисто емкостной цепи, опреде-


изменяется по закону синуса с двойной частотой. Средняя мощность в этой цепи, опре-деляемая по формуле



|
|
|
|
|

|
|
ское поле убывает, убывает и накопленная в первую четверть периода энергия, которая отправляется обратно к источнику.
В третью четверть периода будет то же, что и в первую четверть, только поляр-ность электрического поля конденсатора будет обратной.
| |||||
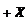 | |||||
| |||||


2.1.12. Последовательное соединение активного сопротивления и емкости
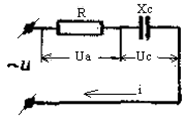 На рис. 2.22 показана цепь с последовательным со-единением активного сопротивления и емкости.
На рис. 2.22 показана цепь с последовательным со-единением активного сопротивления и емкости.
Напряжение на активном сопротивлении называется активным падением напряжения. Оно обозначается как Ua и по закону Ома равно произведению тока на активное
Рис. 2.22
сопротивление. Это напряжение совпадает по фазе с то-ком. Напряжение на емкости называется емкостным паде-нием напряжения и по закону Ома равно произведению тока на емкостное сопротивление:
UC IXC.
Емкостное напряжение отстает по фазе от тока на четверть периода.
Общее напряжение U равно сумме напряжений на последовательно соединенных сопротивлениях. Так как расчет ведется для действующих значений, то это должна быть геометрическая сумма.
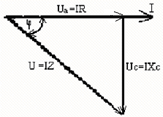 На рис. 2.23 она представлена как сумма векторов
На рис. 2.23 она представлена как сумма векторов

 напряжений Ua и Uc. Полученный прямоугольный тре-угольник называется треугольником напряжений. Из дан-ной векторной диаграммы следует, что при последова-
напряжений Ua и Uc. Полученный прямоугольный тре-угольник называется треугольником напряжений. Из дан-ной векторной диаграммы следует, что при последова-
тельном соединении активного сопротивления и емкости напряжение отстает по фазе от тока на угол f. Активное,
реактивное и полное напряжения связаны между собой как стороны прямоугольного треугольника. На основании того же треугольника напряжений можно написать следующее:
Рис. 2.23



|
|
U = U.
2 2
c

|
ся полным сопротивлением.
Если каждую сторону треугольника напряжений разделить на ток, то получим тре-угольник сопротивлений (рис. 2.24). Из этого треугольника следует:





|
|
|
|
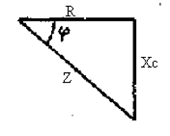
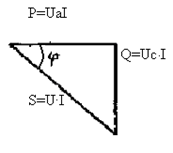 Рис. 2.24 Рис. 2.25
Рис. 2.24 Рис. 2.25
Если каждую сторону треугольника напряжений умножить на ток (а треугольник со-противлений умножить на квадрат тока), то получим треугольник мощностей (рис. 2.25).
| |||||||
| |||||||
| |||||||



2.1.13. Последовательное соединение активного сопротивления, индуктивности и емкости
На рис. 2.26 изображена рассматриваемая цепь. Здесь возможны три характерных случая, каждый из которых следует рассмотреть отдельно.
1. XL > XC.
Напряжения на каждом сопротивлении подсчитываются по известным формулам
Ua = IR, UL IXL, UC = IXC.
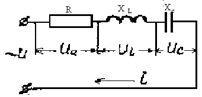 Общее напряжение находится как геометрическая сумма напряжений на отдельных участках. Сложение це-лесообразно вести по правилу многоугольника (рис. 2.26).
Общее напряжение находится как геометрическая сумма напряжений на отдельных участках. Сложение це-лесообразно вести по правилу многоугольника (рис. 2.26).
Одним катетом получившегося прямоугольного треугольника является разность индуктивного и емкост-ного падений напряжений, которая называется реактив-
ным напряжением: Рис.2.26
Up UL − UC.
Поскольку
UL = IXL, UC = IXC, следовательно,
UP = IXL IXc I (XL − Xc) = IX.
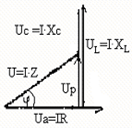 Разность индуктивного и емкостного сопротивлений обозна-чается буквой X и называется реактивным сопротивлением. Не-трудно видеть, что XL и Xc являются частными случаями реак-тивного сопротивления, поэтому они часто называются реактивными сопротивлениями соответственно индуктивности или емкости. На реактивном сопротивлении, в отличие от актив-ного сопротивления, нет расхода энергии.
Разность индуктивного и емкостного сопротивлений обозна-чается буквой X и называется реактивным сопротивлением. Не-трудно видеть, что XL и Xc являются частными случаями реак-тивного сопротивления, поэтому они часто называются реактивными сопротивлениями соответственно индуктивности или емкости. На реактивном сопротивлении, в отличие от актив-ного сопротивления, нет расхода энергии.
Рис.2.27 Из построенной векторной диаграммы (рис. 2.27) следует:



|
откуда
I = U =
R 2 X 2
U
 R 2 +(XL − XC)2
R 2 +(XL − XC)2
U = U.
R 2 +(w L − w C)2
Последнее равенство выражает закон Ома для общего случая последовательного соединения. Ранее полученные выражения закона Ома были частными случаями. Актив-ная и полная мощности для такой цепи подсчитываются по тем же формулам, которые указывались ранее.
Реактивная мощность в общем случае подсчитывается по формуле
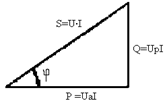 Q = UPI = I 2 X = S ×sinf = UI ×sinf.
Q = UPI = I 2 X = S ×sinf = UI ×sinf.
Физический смысл полной, активной и реактивной мощностей такой же, какой приводился ранее. Треугольник мощностей показан на рис. 2.28.
2. XC > XL.
Рис. 2.28
| |||||||
| |||||||
| |||||||



Находим напряжения на каждом сопротивлении:
Ua IR, UL IXL, UC = IXC.
Так как XC > XL, то UC > UL.
Общее напряжение найдем как геометрическую сумму напряжений на каждом участ-
ке, для чего построим векторную диаграмму напряжений (рис. 2.29). Из векторной диа-граммы напряжений видно, что в этой цепи ток опережает напряжение по фазе на угол f.
Первым катетом получившегося угольника является активное падение
прямоугольного тре-напряжения Ua = IR.
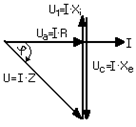 Вторым катетом прямоугольного треугольника является раз-ность индуктивного и емкостного напряжений, которая назы-вается реактивным напряжением. Это напряжение принято рассчитывать по формуле
Вторым катетом прямоугольного треугольника является раз-ность индуктивного и емкостного напряжений, которая назы-вается реактивным напряжением. Это напряжение принято рассчитывать по формуле
Рис.2.29 Up = UL UC.
В данном случае оно получится отрицательным, что и будет указывать на преобла-дание емкостного сопротивления над индуктивным. Если же реактивное напряжение бу-дет со знаком плюс, то это указывает на то, что индуктивное сопротивление больше ем-костного. Так как UL = IXL, а Uc = IXc, то
Up = IXL − IXC = I (XL XC) = IX,
где X = XL − XC называется реактивным сопротивлением. В данном случае оно будет иметь знак минус, что опять указывает на преобладание емкостного сопротивления над ин-дуктивным. Если же реактивное сопротивление положительное, то индуктивное сопротив-ление больше емкостного. Общее напряжение найдем из прямоугольного треугольника:



|
Решим это уравнение относительно тока I. В итоге получим выражение
I = U =
R 2 X 2
U
 R 2 +(XL − XC)2
R 2 +(XL − XC)2
U = U.
R 2 +(w L − w C)2
Последние равенства выражают закон Ома для данной цепи. Вид этих формул та-кой же, какой получен в условии XL > XC. Это указывает на то, что наконец получена
формула закона Ома, выражающая общий случай и пригодная для расчета любой после-
довательной цепи. Здесь R =å R, XL =å XL, XC = XC, а под полным сопротивле-
нием z надо понимать следующее:
 z = å R 2 +(å XL −å XC)2. 3. XL = XC (резонанс напряжений).
z = å R 2 +(å XL −å XC)2. 3. XL = XC (резонанс напряжений).
При XL = XC будем иметь следующие равенства: Ua = IR, UL = IXL, UC = IXC,



|
|
В такой цепи ток и напряжение совпадают по фазе. Цепь по отношению к источни-ку ведет себя так, как будто бы в ней нет ни индуктивности, ни емкости. На рис. 2.30 приведена векторная диаграмма и графики напряжений и тока данной цепи. Рассмот-ренный случай получил название резонанса напряжений.
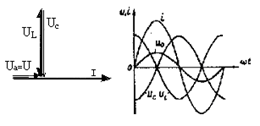 Резонанс напряжений возникает при по-следовательном соединении индуктивности и емкости, если индуктивное сопротивление равно емкостному сопротивлению. Это означа-ет равенство энергий магнитного и электриче-ского полей.
Резонанс напряжений возникает при по-следовательном соединении индуктивности и емкости, если индуктивное сопротивление равно емкостному сопротивлению. Это означа-ет равенство энергий магнитного и электриче-ского полей.
Равенство энергий обусловлено равенст-
вом реактивных мощностей индуктивности Рис.2.30
и емкости:
|
|
|
При резонансе напряжений общее напряжение равно напряжению на активном сопро-тивлении. Общее сопротивление равно активному сопротивлению, ток и напряжение сов-падают по фазе. При резонансе напряжений напряжения на индуктивности и емкости могут быть во много раз больше напряжения источника, что является вредным в технике сильных токов, так как возможен пробой изоляции трансформаторов, реакторов и кабелей.
В технике слабых токов (радиотехнике) на использовании резонанса напряжений работает целый ряд устройств.
2.1.14. Физическая сущность явлений, возникающих при резонансе
Если электрическая цепь обладает индуктивностью, то она сосредоточивает маг-нитное поле. В такой цепи напряжение опережает ток на угол f. В цепи, обладающей
емкостью, сосредоточивается электрическое поле. В такой цепи ток опережает напряже-ние на угол f.
Следовательно, действие магнитного поля противоположно действию электриче-ского поля на фазовые соотношения тока и напряжения. Если же цепь одновременно об-ладает
|
|
|
|
|
Дата добавления: 2014-10-15; Просмотров: 2175; Нарушение авторских прав?; Мы поможем в написании вашей работы!