
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Множення вектора на число
|
|
|
|
Віднімання векторів.
Означення 2.Сумою декількох векторів називається вектор, початок якого співпадає з початком першого, а кінець - з кінцем останнього, причому кожний наступний вектор має початок в кінці попереднього.
Додавання векторів.
Означення 1. Сумою двох векторів 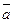 і
і 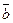 називається третій вектор, початок якого співпадає з початком вектора
називається третій вектор, початок якого співпадає з початком вектора 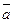 , а кінець з кінцем вектора
, а кінець з кінцем вектора 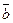 , причому початок
, причому початок 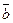 виходить із кінця.
виходить із кінця.
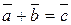 .
.
Сума двох неколінеарних векторів 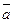 і
і 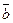 можна знаходити правилом трикутника або паралелограму.
можна знаходити правилом трикутника або паралелограму.

Сума 3-х некомпланарних векторів 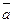 ,
, 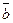 ,
, 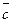 за правилом паралелепіпеда
за правилом паралелепіпеда
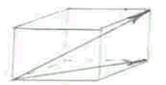
 |
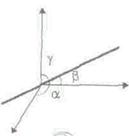
Означення 3. Різницею двох векторів
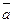 і
і 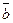 (зведених до спільного початку 0) називається вектор, напрямлений із кінця від’ємника (вектора
(зведених до спільного початку 0) називається вектор, напрямлений із кінця від’ємника (вектора 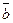 ) в кінець зменшуваного (
) в кінець зменшуваного (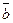
 ).
).
|
Означення 4. Добутком вектора 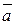 на число m називається вектор
на число m називається вектор 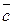 , який задовольняє наступним умовам:
, який задовольняє наступним умовам:
1) довжина вектора 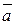 дорівнює добутку довжини
дорівнює добутку довжини 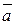 на модуль числа m;
на модуль числа m;
2) якщо m >0, то 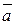 і
і 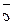 співнапрямлені, якщо m< 0, то
співнапрямлені, якщо m< 0, то 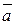 і
і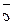 - протилежно напрямлені.
- протилежно напрямлені.

|
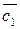
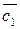 =ma, m>0
=ma, m>0
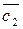 =ma, m<0
=ma, m<0
Властивості добутку вектора на число.
1) 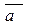 × 1=
× 1= 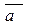 ,
, 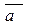 × 0=0;
× 0=0;
2) a (b ×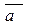 )=(a × b)
)=(a × b) 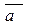 ;
;
3) (a × b) 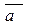 = a ×
= a × 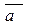 + b ×
+ b × 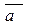 ;
;
4) a (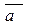 +
+ 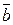 )= a
)= a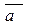 + a
+ a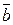 .
.
(Довести одно самостійно)
§3 Орт вектора. Умова колініарності.
Означення 1. Вектор, модуль якого дорівнює 1, називається ортом (одиничним вектором).
Означення 2. Ортом ненульового вектора 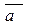 називається вектор, модуль якого дорівнює 1, а напрямок співпадає з напрямком вектора 1,
називається вектор, модуль якого дорівнює 1, а напрямок співпадає з напрямком вектора 1, 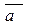 0 ||
0 || 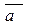 .
.
Справедлива рівність: 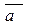 =
= 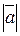
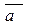 0;
0; 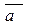 0=
0= 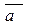 /
/ 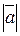 .
.
Теорема 1. (ознака колініарності 2-х векторів).
Для того, щоб два вектори були колінеарні необхідно і достатньо, щоб один із них дорівнював добутку деякого числа на другий вектор.
Нехай вісь 1 утворює з осями координат кути a,b,g. Напрямними косинусами осі 1 (або напрямку 1) називаються косинуси цих кутів (cos a, cosb, cosg)
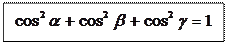 Якщо напрямок заданий одиничним вектором
Якщо напрямок заданий одиничним вектором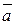 , то напрямні косинуси являються його координатами n0(cos a, cosb, cosg). Напрямні косинуси зв'язані між собою співвідношенням:
, то напрямні косинуси являються його координатами n0(cos a, cosb, cosg). Напрямні косинуси зв'язані між собою співвідношенням:
§4. Лінійна залежність, та незалежність векторів.
Означення 1. Вектори 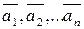 називаються лінійно залежними, якщо існують такі числа осі,
називаються лінійно залежними, якщо існують такі числа осі, 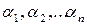 одночасно не всі рівні нулю що
одночасно не всі рівні нулю що 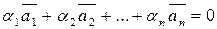 . В протилежному випадку вектори називаються лінійно-незалежними.
. В протилежному випадку вектори називаються лінійно-незалежними.
Якщо вектори 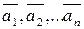 лінійно залежні і наприклад
лінійно залежні і наприклад 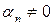 , тоді
, тоді 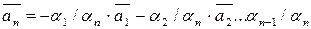 тобто,
тобто, 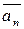 - являється лінійною комбінацією векторів
- являється лінійною комбінацією векторів 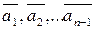 .Таким чином, якщо вектори лінійно-залежні, то хоч один із них лінійно виражається через решту векторів. Геометрично:
.Таким чином, якщо вектори лінійно-залежні, то хоч один із них лінійно виражається через решту векторів. Геометрично:
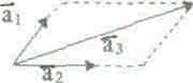
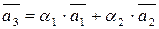
Теорема 1. (про лінійну залежність 2-х векторів).
Два, вектори лінійно-залежні тоді і тільки тоді, коли вони колінеарні.
Доведення: 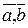 - лінійно-залежні Þ
- лінійно-залежні Þ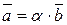 , тоді за ознакою колініарності
, тоді за ознакою колініарності 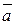 úú
úú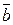 . щ.п.д.
. щ.п.д.
Теорема 2. (про лінійну залежність 3-х векторів).
Три вектори 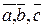 лінійно-залежні тоді і тільки тоді, коли вони колінеарні.
лінійно-залежні тоді і тільки тоді, коли вони колінеарні.
Доведення: 1) Необхідність.
Нехай 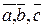 , лінійно залежні, покажемо, що вони компланарні. З того, що вектори лінійно залежні можемо записати
, лінійно залежні, покажемо, що вони компланарні. З того, що вектори лінійно залежні можемо записати 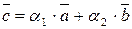 :
:
а) 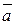 úú
úú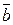 , то
, то 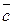 лежить з ними на одній прямій тоді
лежить з ними на одній прямій тоді 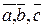 - компланарні.
- компланарні.
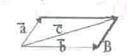
б)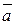 úú
úú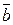 , тоді за правилом паралелограма маємо, що всі вектори лежать в одній
, тоді за правилом паралелограма маємо, що всі вектори лежать в одній 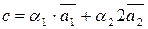 площині Þ компланарні.
площині Þ компланарні.
2) Достатність.
Нехай 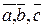 компланарні, покажемо, що вони лінійно залежні.
компланарні, покажемо, що вони лінійно залежні.
а) 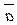 úú
úú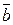 Þ
Þ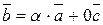 Þ
Þ 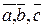 лінійно залежні.
лінійно залежні.
|
б) 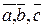 - попарно колінеарні.
- попарно колінеарні. 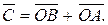
1) 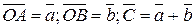
2) 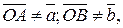 тоді
тоді 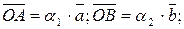
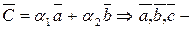 лінійно залежні.
лінійно залежні.
Наслідок: 1. три компланарні вектори лінійно незалежні.
2. чотири вектори в трьохмірному лінійному просторі лінійно залежні завжди.
Теорема 3. Якщо два вектори 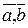 не колінеарні, то будь-який вектор
не колінеарні, то будь-який вектор 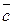 що лежить в площині векторів
що лежить в площині векторів 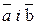 , можна лінійно виразити через вектори
, можна лінійно виразити через вектори 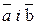 єдиним способом.
єдиним способом.
Доведення: 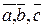 -компланарні (за умовою), тоді існують такі числа
-компланарні (за умовою), тоді існують такі числа 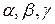 одночасно не рівні нулю, то
одночасно не рівні нулю, то 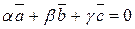 . Розглянемо два випадки:
. Розглянемо два випадки:
а) нехай, наприклад, g = 0, тоді 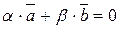 Þ
Þ 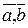 - лінійно залежні.
- лінійно залежні.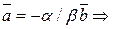
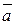 úú
úú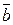 .
.
б)g¹0, 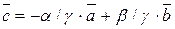 , або
, або 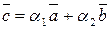 (1) так як
(1) так як 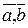 лінійно незалежні, то
лінійно незалежні, то 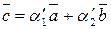 (2)
(2) 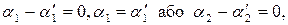
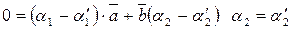 .
.
Теорема 4. Якщо три вектори 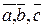 - не компланарні, то будь-який вектор
- не компланарні, то будь-який вектор 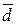 можемо лінійно виразити через
можемо лінійно виразити через 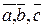 , при тому єдиним способом.
, при тому єдиним способом.
§5. Базис і координати вектора.
Означення 1. Множину найрізноманітніших систем (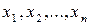 ), дійсних чисел називають n - мірним дійсним простором і позначають через Rn.
), дійсних чисел називають n - мірним дійсним простором і позначають через Rn.
Кожну таку систему чисел назвемо точкою або вектором Rn, числа х1... хn- координати точки (вектора) або компоненти вектора.
Означення 2. Сукупність “n” лінійно незалежних векторів n - мірного простору називається його базисом.
Зауваження: Простір називається лінійним векторним, якщо в ньому визначені операції додавання векторів і множення на число.
Теорема 1. Кожен вектор 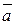 лінійного n-мірного простору можна представити єдиним способом у вигляді лінійної комбінації векторів базису
лінійного n-мірного простору можна представити єдиним способом у вигляді лінійної комбінації векторів базису 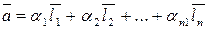
Числа a1, a2…an - називаються координати вектора 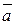 в базис
в базис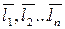 ? тобто
? тобто 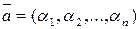 .
.
|
|
|
|
|
Дата добавления: 2014-10-15; Просмотров: 1316; Нарушение авторских прав?; Мы поможем в написании вашей работы!