Пряма в просторі

1. Загальні рівняння прямої в просторі

Лінію в просторі ми будемо розглядати як множину всіх точок, що належать кожній із двох площин, які перетинаються. Якщо ці поверхні задані рівнянням F(x,y,z) = 0, то Ф(x,y,z) – лінія їх перетину визначається системою рівнянь:

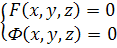
Означення 1: Пряма в просторі являється лінією перетину двох площин, тому аналітично її можна задати системою

(1)

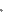Приклад:

M₁

M₂

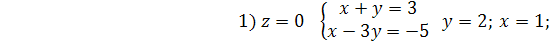
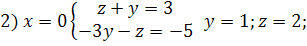
2.Векторне рівняння прямої та параметричне рівняння прямої

Положення прямої в просторі визначається, якщо задати будь-яку її фіксовану точку 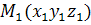та вектор 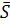паралельний цій прямій.

Означення 2: Вектор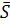називається напрямленим вектором прямої, якщо він лежить на ній або паралельний цій прямій.

Нехай пряма L задана точкою M₁ та 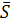(m,n,p). Візьмемо на прямій L довільну т. М(x,y,z).

Тоді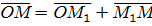

або

(2)

;

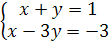
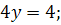
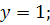
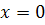Означення 3: Рівняння (2) називається векторним рівнянням прямої.

Запишемо рівняння (2) в векторній формі:

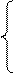
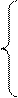
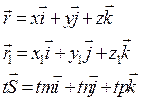
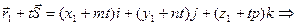
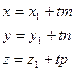(3)

Рівняння (3) – параметричні рівняння прямої.

3.Канонічні рівняння прямої

Нехай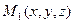лежать на L і S (m,n,p)– її напрямлений вектор. Візмемо на L будь-яку

L точку, тоді M║S 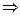їх координати пропорційні

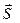
M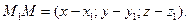

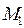
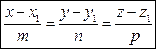(4) канонічні рівняння прямої

Зауваження: Канонічні рівняння можна отримати знаючи координати двох точок 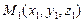і 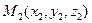, які лежать на прямій так як за напрямлений вектор можна вважати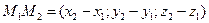

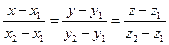
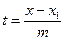
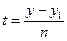
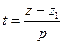
Канонічні рівняння прямої (4) можна отримати із параметричних рівняннь (3) виключення параметра t або (5)

Приклад: Скласти каннічне рівняння прямої

.

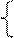
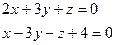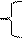Знайдемо координати 2-х точок z = 0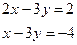

x=6 y=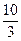

;

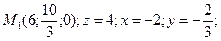
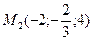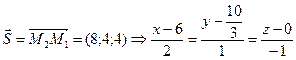
Щоб перейти від загального р-ня прямої (1) до іншого вигляду потрібно знайти т.ML та.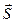

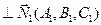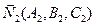Так як пряма та то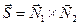

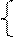Приклад: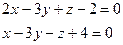

.

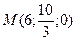
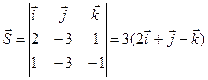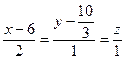
4.Кутові співвідношення

Знаючи напрямлені вектори можливо знаходити кут між ними, кут між прямою та площиною.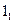

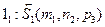
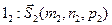
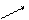
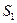
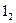
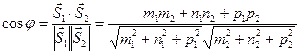
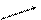
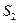
┴ - і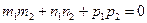

║- і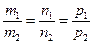

а) l ┴ α; якщо ║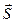

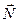
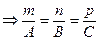
б) l║α; якщо ┴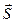

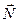
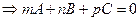
в)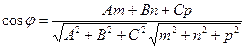

5.Відстань від точки до прямої

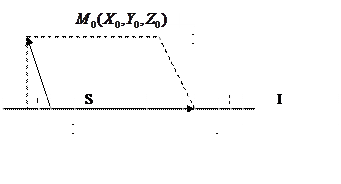Розглянемо т. 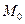і пряму l.Візьмемо довільну точку прямої l M(x,y,z). Тоді площа паралелограма :

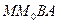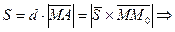
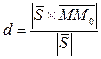
(6)

Приклад: Знайти відстань від т. 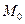(1;-1;2) до прямої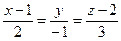

Розв’язування: 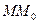= (0;-1;0) т.к. M(1;4;2) S(2;-1;3) |S| =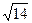

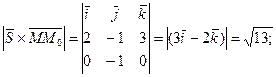
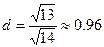
Дата добавления: 2014-10-15