Поверхні другого порядку

Параметричне рівняння лінії

Інколи заміст рівнянь ліній, які повязують прямокутні координати 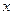та , розглядають параметричні рівняння. Які визначають змінні величини 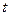(параметра). Наприклад в механіці т. 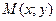є функція від часу .

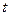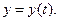
Розглянемо параметричне рівняння кола, коло .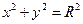

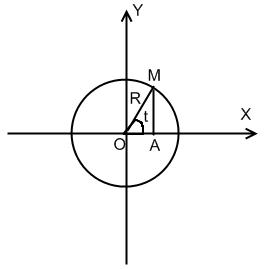
В .

Рівняння кола:

,

Рівняння еліпса:

Приклад: побудувати криву ; ; 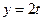. 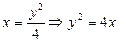- парабола.

t	-2	-1	0	1	2…
x	4	1	0	1	4…
y	-4	-2	0	2	4…

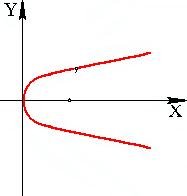
2) ,

t
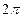
x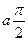
y

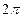
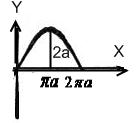
1. Сфера

Означення 1. Сферою радіуса називаэться множина всых точок простору,

відстань від кодної до даної точки (центру) дорівнює .

При .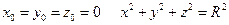

Приклад: визначити координати 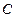і . .

2. Циліндричні поверхні

Означення 2. Поверхня, що скдадається з усіх прямих, що перетинають дану

лінію називається циліндричною поверхнею.

Еліптичний циліндр: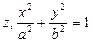

Круговий циліндр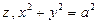

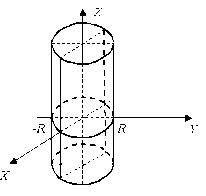
Параболічний циліндр: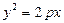

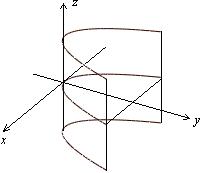
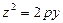
Гіперболічний циліндр: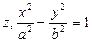

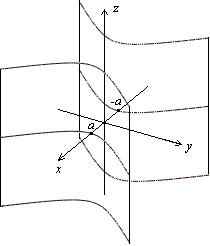
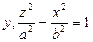
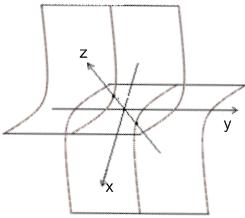
3. Конічні поверхні

Означення 3: поверхня, яка складається з усіх прямих, що перетинають дану

лінію і проходять через дану т. 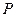називається конічною.

Конус - еліптичний

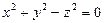- круговий

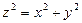
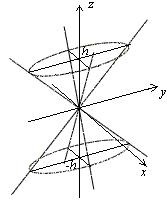
4. Поверхні обертання

Еліпсоїд

Гіперболоїди

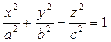
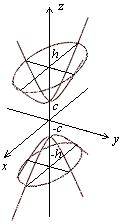
Параболоїд

Гіперболічний параболоїд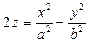

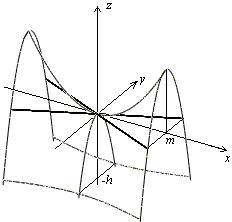
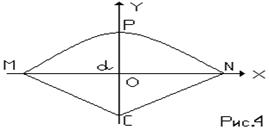Пример 6. Сегментная арка имеет вид или форму дуги окружности (рис. 4). Составить уравнение этой окружности, найти положение ее центра и радиус, если пролет арки L = MN= 20, а ее подъем, т.е. отношение ее высоты кпролету, ,

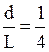Решение. По условию L=20м, , следовательно d=5м. В выбранной системе коор­динат точки M, N, P имеют соответcтвенно координаты (-10;0), (10;0), (0;5). В силу симметрии арки относительно оси Oy центр искомой окруж­ности т. С лежит на оси Oy.

Запишем уравнение окружности: .

Поскольку окружность проходит через точки M и P, можем записать систему:

;

Решив ее, получим R=12,5, Y₀=-7.5.

Таким образом, центром окружности является точка C (0;-7,5),а ее радиус –R=12,5. Уравнение

окружности имеет вид:

.

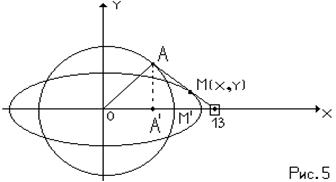Пример 7. Кривошип OA вращается с поcтоянной угловой скоростью w=10 рад/c и приводит в движение ползун B с помощью шатуна AB,причем OA=AB=80см (рис.5). Составить уравнение траек­тории средней точки М шатуна изобразить эту траекторию на рисунке.

Решение. Используя рис. 5, находим Из . .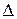

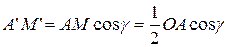
Тогда ; .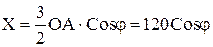

Поскольку угловая скорость кривошипа OA постоянна, то

Где t - время

Полученные уравнения являются параметрическими уравнениями траектории точки М.

Исключив параметр t, получим каноническое уравнение траектории:

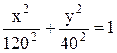
Это элипс с полуосями 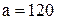, изображенный на рис.5.

Розділ 4. ЕЛЕМЕНТИ МАТЕМАТИЧНОГО АНАЛІЗУ.

1.ФУНКЦІЯ

Озн.1 Величина у – наз. функцією від величини х, якщо за певним правилом f,кожному значенню величини х відповідає єдине цілком визначене значення величини у. Х –наз. аргументом, або незалежною змінною, у-залежною змінною. В даному випадку записують у = f (х).

f-правило за яким 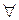х відповідає 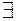! у.

Способи завдання функції:

1) Аналітичний – у =f (х)

Х ^{……………………………}

2) Табличний У ^{……………………………} (табулювати) це приблизний.

3) Графічний

Озн.2 Графіком функції у =f (х) – наз. множину всіх точок М(х,у) площини ОХУ, координати яких зв’язані данною функціональною за-лежністю.

Озн.3 Якщо кожному значенню х відповідає одне значення у, то у=f(х)-наз. однозначною ф-цією (у = sinx, y =x²), якщо хоча б деяким значенням х відповідає декілька або нескінчена множина значень змінної у, то у – наз. багатозначною ф-єю від х (наприклад у = arcsin x).

Основні елементарні функції

1) степенева ф-ія у = х _______ _______ _______ _______

>1 <1 0<<1 у = х^{1/ 3}

2)показникова у = а^х

3)логарифмічна у = log _ах

4)тригонометричні

Взаємообернені функції.

Нехай дана функція (1) у = f(х), х є [а, в], х є [c, d ], тоді у = (х) або у = (у) (2) буде взаємооберненою відносно у = f(х). Графіки взаємообернених ф-цій симетричні відносно прямої у = х (бісектриси 1 і 3 коор. кутів)

у=f(х)

у = (х)

Обернені тригонометричні ф-ії.

y = arcsin x y = arctg x

Y = arcctg x

y = arccos x

Складна ф-ція (суперпозиція ф-ції)

Х U u = (x)

f q y = g (u)

Y y = f (x) = g(u) = g((x))

Y =g- суперпозиція ф-ії

Наприклад: y = sin u, u = x², y = sin x²

Неявні функції

Озн.4 Функція наз. явною, якщо вона задана формулою, права частина якої не містить залежної змінної (y = x², …), і наз-ся неявною, якщо вона задана рівнянням F(x,y) = 0 (1), яке не розв’язане відносно y.

(x ² + y² = 1)

Зауваження Не всяке р-ня (1) визначає неявну функцію. Наприклад

x² + y² + 1 = 0 в області дійсних чисел функцію не виз-

начає.

Елементарні функції

Озн.5 Функція у =f (х) наз-ся елементарною, якщо вона може мати вигляд одного аналітичного виразу з кінцевим числом арифметичних дій над основними елементарними ф-ями.

ln²x_

(y= ctg x²+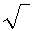x²+4 - 5) – елем.

у=| x | = ² –не явл. т.як | ~ |- не вход. в ариф. дії

До елементарних ф-цій відносяться:

а) раціональні у = Pn (x) = A ₀x⁴+ … +A _n-1 +A _n

у = ах + b, y = ax²+ bx +c

Рn (x) 1_

б) дробово-раціональні у = Qm(x), де Pn (x), Qm (x)- многочлени (у= х)

е^х - е^-х у=sh x

в) гіперболічні: sh x = 2

e^x + e^-x y = ch x

ch x = 2

1

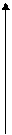sh x_e^x – e ^-x_ _ _ _ _ _ _ 1 _ _ _ _ _

th x = ch x = e^x +e ^–x

_ _ _ _ _ _ -1 _ _ _ _ _

ch x_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _

cth x = sh x

_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _

Властивості: ch² x – sh² x = 1

sh (x 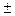y) = sh x _* ch y 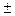sh y _* ch x

ch (x +y) = ch x _* ch y + sh x _* sh y

(Дома повторити елементарні функції: парну, непарну, періодичну та

їх графіки).

Дата добавления: 2014-10-15