
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Властивості границь функції
|
|
|
|
1.Якщо існує lim f(x), то f(x) обмежена.

2. Якщо f(x) при x a має границю, то вона єдина.
a має границю, то вона єдина.
3. Якщо існує lim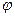 (x)=A i lim q(x)=A, то lim f(x) A, де
(x)=A i lim q(x)=A, то lim f(x) A, де 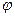 (х)
(х)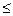 f(x)
f(x)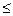 q(x).
q(x).



4. Якщо існує lim f1 (x)=A1 i lim f2 (x)=A2 i f1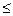 f2 x
f2 x  u (a) =>
u (a) =>


lim f1(x) 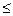 lim f2 (x)
lim f2 (x)


5. Якщо 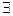 lim f(x) i q(x), x
lim f(x) i q(x), x a, то
a, то
а) lim (f(x) 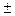 q(x)) = lim f(x)
q(x)) = lim f(x)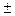 lim q(x)
lim q(x)
б) lim f(x) q(x) = lim f(x)
q(x) = lim f(x) lim q(x)
lim q(x)
в) lim C f(x) = C lim f(x)
г)

6. lim C = C

7.lim f(x) = f(lim x)


Дов. 1-ого 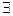 u (a) таке, що 1> |f(x)-A|
u (a) таке, що 1> |f(x)-A|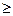 |f(x)|-|A|, (x
|f(x)|-|A|, (x  u(a), x
u(a), x a)
a)
|f(x)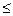 1+|A|, де M = 1+|A| => f(x)- обмежена
1+|A|, де M = 1+|A| => f(x)- обмежена
5. НЕСКІНЧЕННО МАЛІ ТА НЕСКІНЧЕННО ВЕЛИКІ ФУНКЦІЇ.
 Озн.1 Якщо lim f(x) = 0, то f(x), є н.м., а якщо lim f(x) =
Озн.1 Якщо lim f(x) = 0, то f(x), є н.м., а якщо lim f(x) = 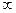 ,
,


f(x)-нескінченно велика.
Як і для послідовностей має місце твердження. Якщо ф-я н.м. при x a i f(x)
a i f(x) 0
0 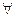 x
x a з будь-якого околу а, то ф-я
a з будь-якого околу а, то ф-я 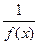 - н.в. при x
- н.в. при x a і навпаки.
a і навпаки.
Теорема (зв’язку границі функції і н.м.)
Для того, щоб число А було границею ф-ї f(x) при  необхідно і достатньо, щоб ф-я f(x) була рівна сумі числа А і
необхідно і достатньо, щоб ф-я f(x) була рівна сумі числа А і 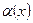 , де
, де
lim 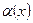 =0 –н.м.
=0 –н.м.

Доведення.
Необхід. lim f(x) = A => f(x) = A+  (x),
(x),  (x)-н.м. За означ. lim f(x)=A
(x)-н.м. За означ. lim f(x)=A


=>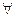 E>0
E>0 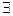
 >0 |f(x)-A| <E, |x-a| <
>0 |f(x)-A| <E, |x-a| <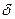 =>за озн. 5 ф-ції f(x)-A=
=>за озн. 5 ф-ції f(x)-A= 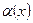
 (x)-н.м. f(x)= A+
(x)-н.м. f(x)= A+ (x)
(x)
Достат. f(x) =A+ (x) де
(x) де  (x) – н.м. при x
(x) – н.м. при x a => lim f(x)= A
a => lim f(x)= A

lim f(x) = lim (A+ (x)) = lim A +lim
(x)) = lim A +lim  (x)= A+0=A
(x)= A+0=A




Порівняння нескінченно малих
Розглянемо 2 ф-ії 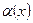 та
та 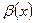 , які задані в деякому проміжку U(x0), за винятком можливо самої т. x0, x0, може бути скінченною або нескінченною.
, які задані в деякому проміжку U(x0), за винятком можливо самої т. x0, x0, може бути скінченною або нескінченною.



 Нехай
Нехай 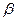 (x)
(x)  0 на U(x0) ____________________________
0 на U(x0) ____________________________
 U(x0)
U(x0)
Озн.2 Фун-ії 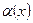 та
та 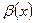 наз. Нескінченно малими одного і того ж порядку малості при x
наз. Нескінченно малими одного і того ж порядку малості при x x0, якщо
x0, якщо 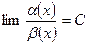


Озн.3 Ф-ія 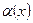 наз. нескінченно малою ф-єю більш високого порядку малості, ніж
наз. нескінченно малою ф-єю більш високого порядку малості, ніж 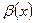 при x
при x x0, якщо
x0, якщо  ;
;

І більш низького порядку малості, ніж 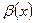 , якщо
, якщо 


 Озн.4 Ф-ії
Озн.4 Ф-ії 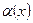 та
та 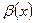 наз. непорівняними, н.м.ф. при x
наз. непорівняними, н.м.ф. при x x0, якщо
x0, якщо  не існує і не дорівнює
не існує і не дорівнює 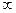 .
.
Озн.5 Ф-ії 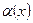 та
та 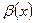 - н.м. при x
- н.м. при x x0 наз. еквівалентними, якщо
x0 наз. еквівалентними, якщо  т.б.
т.б. 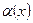 ~
~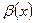

Таблиця еквівалентності н.м.ф.
1)  ~
~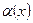 5) e
5) e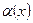 -1~
-1~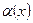
2)  6) b
6) b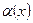 -1~
-1~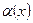 ln b
ln b
3) 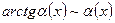 7) ln (
7) ln ( (x)+1)~
(x)+1)~ (x)
(x)
4)  8) (1+
8) (1+ (x))p-1~ p
(x))p-1~ p
 (x)
(x)
Приклад 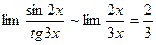


Властивості б/м ф-ї
1. Алгебраїчна сума зкінченного числа н.м. ф-ій є ф-я н.м.
2. Добуток скінченого числа н.м. ф-ій є ф –я н.м.
3. Добуток н.м. ф-ї на обмежену є ф-я н.м.
Розкриття невизначених виразів:
 ділення чисельника та знаменника на найвищу степінь х.
ділення чисельника та знаменника на найвищу степінь х.
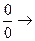 скоротити чисельник та знаменник на х-а
скоротити чисельник та знаменник на х-а
а) перетворенням виразів чисельника та знаменника
б) домноженням на спряжене знаменник та чисельник
в) використання таблиці еквівалентів н.м.
г)використання 1-ї чудової границі.
 використання 2-ї чудової границі.
використання 2-ї чудової границі.
Всі інші перетворюються в ці оснсвні.
 6. НЕПЕРЕРВНА ФУНКЦІЯ
6. НЕПЕРЕРВНА ФУНКЦІЯ
Озн.1 Ф-я f(x), x [a,b] наз-ся неперервною в x0
[a,b] наз-ся неперервною в x0  [a,b], якщо границя ф-ї f(x) в т.x0 iснує і дорівнює значенню ф-ї в цій точці: lim f(x)=lim f(x0)
[a,b], якщо границя ф-ї f(x) в т.x0 iснує і дорівнює значенню ф-ї в цій точці: lim f(x)=lim f(x0)


 Озн.2 Ф-я f(x) наз. неперервною в т.x0, якщо вона визначена в околі точки і границя приросту функції в цій точці дорівнює 0, якщо
Озн.2 Ф-я f(x) наз. неперервною в т.x0, якщо вона визначена в околі точки і границя приросту функції в цій точці дорівнює 0, якщо 
y



 y _ _ _ _ _ _ _ _ _ _
y _ _ _ _ _ _ _ _ _ _


 lim
lim  f(x) = 0 y0_
f(x) = 0 y0_ y _ _ _ _ _ _ _
y _ _ _ _ _ _ _





 |  |
 0 x0
0 x0  x x x
x x x
 Озн.3 Ф-я f(x) наз. неперервною зліва в т. x0, якщо lim f(x)=f (x0) і
Озн.3 Ф-я f(x) наз. неперервною зліва в т. x0, якщо lim f(x)=f (x0) і
 -0
-0
неперервною справа, якщо lim f(x)= f(x0)
 +0
+0
 Озн.4. Ф-я f(x) наз. неперервною на будь-якому інтервалі (a,b),якщо вона неперервна в кожній точці цього інтервалу.
Озн.4. Ф-я f(x) наз. неперервною на будь-якому інтервалі (a,b),якщо вона неперервна в кожній точці цього інтервалу.
Властивості функції неперервної в точці на відрізку
1. Сума скінченого числа ф-ій, неперервних на будь-якому проміжку (а,в) у точці х0, є ф-я неперервна в цій точці.
2. Добуток скінченого числа ф-й, неперервних в точці х0, є неперервна ф-я в точці ч0.
3. Частика двох функцій, неперервних в точці х0 є ф-я неперервна в т.х0, якщо значення ф-ії в знаменнику не дорівнює 0 в х0.
4. Якщо f(x) неперервна то lim f(x) = f (lim x)


5. Якщо ф-я f(x) неперервна на [a,b] і на його кінцях приймає значення різних знаків, то на [a,b] знайдеться хоча б одна точка, в якій ф-я дорівнює 0.
6.Якщо ф-я неперервна на [a,b] то на ньому існує найбільше i найменше значення функції.
|
|
|
|
|
Дата добавления: 2014-10-15; Просмотров: 610; Нарушение авторских прав?; Мы поможем в написании вашей работы!