Задачи контрольной работы

Вопросы для самопроверки

Тема 5. НОРМАЛЬНЫЙ ЗАКОН РАСПРЕДЕЛЕНИЯ СЛУЧАЙНОЙ ВЕЛИЧИНЫ

ЛИТЕРАТУРА: [3], гл. XII, § 1—7, задачи 2—4.

Прежде чем приступить к изучению этой темы, необходи­мо усвоить понятие случайного события, определение вероят­ности случайного события, понятие случайной величины и ее закона распределения. Следует обратить внимание на при­меры дискретных и непрерывных случайных величин, а так­же на принципиальное отличие их друг от друга.

Нормальное распределение играет важнейшую роль в био­логической статистике, поэтому следует хорошо усвоить ос­новные понятия, связанные с этой темой, и научиться рисо­вать эскиз нормальной кривой по заданным параметрам рас­пределения. Для вычисления вероятности попадания нор­мально распределенной случайной величины в заданный ин­тервал используют функцию Лапласа Ф (х). Для этой функ­ции существует несколько разновидностей, с которыми мож­но встретиться в литературе. При использовании таблицы значений функций Лапласа, приведенной в приложении 1, необходимо помнить, что эта функция обладает свойством нечетности Ф(—х) =—Ф(x) и что Ф(x) ~0.5 для любого х>5.

1. Напишите плотность вероятности нормального распре­деления. Какими параметрами определяется нормальное рас­пределение? Каков их вероятностный смысл?

2. Начертите нормальную кривую. Каков геометрический смысл параметров нормального распределения? Как влияет изменение математического ожидания и среднего квадрати­ческого отклонения на форму нормальной кривой?

3. Как вычислить вероятность попадания в заданный ин­тервал значений нормально распределенной случайной вели­чины?

4. В чем заключается правило «трех сигм»? Как найти диапазон изменения значений нормально распределенной случайной величины?

В ЗАДАЧАХ 61-66 предполагается, что промеры телок

являются нормально распределенны­ми случайными величинами с задан­ными параметрами а и 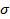. Требуется определить: 1) процент животных, для которых величина промера бу­дет принадлежать заданному интер­валу; 2) диапазон изменения проме­ра.

Номер задачи	Промер X (см)	a		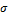Интервал
	Высота в холке		5,4	(110; 120)
	Косая длина туловища		10,8	(125; 135)
	Глубина груди	58,8	3,6	(55; 62)
	Ширина груди	48,7	4,8	(45; 52)
	Обхват груди		8,4	(170; 180)
	Обхват пясти	16,4	4,8	(15; 22)

В ЗАДАЧАХ 67—70 предполагается, что живая масса те­лок X (кг) распределена по нормаль­ному закону с заданными парамет­рами a и 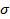. Требуется определить:

процент животных, для которых живая масса будет заключена в указанных пределах; 2) диапазон изменения живой массы.

Номер задачи	Возраст (мес.)	a		Пределы изменения X
			17.4	95-110
			15.6	175-180
			31.8	300-325
			61.2	400-450

Дата добавления: 2014-10-15