Решение типовой задачи

ЗАДАЧИ КОНТРОЛЬНОЙ РАБОТЫ

Вопросы для самопроверки

Тема 7. КОРРЕЛЯЦИЯ И РЕГРЕССИЯ

ЛИТЕРАТУРА: [3], гл. XVIII, §1- 9. задачи 1, 2.

В некоторых исследованиях важно установить, изменяются ли два признака (случайные велечины) независимо друг от друга, или же изменение одного из них каким – то образом связано с изменением другого. На сам факт такой связи (или на ее отсутствие) указывает значение коэффициента корреляции. Уравнение регрессии позволяет предсказать, какие изменения первого признака. Понятия коэффициента корреляции и коэффициента регрессии играют важную роль в совместном изучении двух случайных величин, поэтому необходимо усвоить методику их вычисления.

1. Что понимают под корреляционной зависимостью? Чем она отличается от функциональной зависимости?

2. Что собой представляет корреляционная таблица (кор­реляционная решетка)? В каких случаях целесообразно ее составление?

3. Что такое корреляционное поле?

4. Сформулируйте две основные задачи корреляционного анализа.

5. Что характеризует коэффициент корреляции? Какие значения он может принимать?

6. Что можно сказать о связи между двумя случайными величинами, если коэффициент корреляции равен нулю? ра­вен единице?

7. Какая разница между положительной и отрицательной корреляцией?

8. Как получают эмпирическую линию регрессии?

9. Какую форму имеет линия регрессии в случае линейной корреляционной зависимости?

10. Запишите уравнение прямой регрессии. Как можно построить эту прямую?

11. Что характеризует коэффициент регрессии?

12. При изучении зависимости между живым весом коров - первотелок и их удоями за нормированную лактацию был вычислен коэффициент регрессии b_y/x=6,9_. Какого увеличе­ния удоев в среднем можно ожидать при увеличении веса коров -первотелок на 10 кг?

В ЗАДАЧАХ 81—90 требуется: I) найти коэффициент корреляции и сделать вывод о тес­ноте и направлении линейной корре­ляционной связи между признака­ми; 2) составить уравнение прямой регресии Y на X; 3) нанести на чер­теж исходные данные и построить прямую регрессии.

В таблице 3 представлены данные о длине туши X (см) и толщине шпика Y (мм) для свиней различных пород.

В таблице 4 представлены измерения у 10 телят по глу­бине груди X (см) и живой массе Y (кг).

Таблица 5

№ наблюдения	№ задачи

Таблица 6

№ наблюдения	№ задачи

Задача. Для 10 петушков леггорнов 15-дневного возраста были получены следующие данные о весе их тела X (г) и весе гребня У (мг):

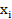83 72 69 90 90 95 95 91 75 70

56 42 18 84 56 107 90 68 31 48.

Требуется:

1) найти коэффициент корреляции и сделать вывод о тес­ноте и направлении линейной корреляционной связи между признаками;

2) составить уравнение прямой регрессии;

3) нанести на чертеж исходные данные и построить полу­ченную прямую регрессии.

Решение. В случае малых выборок расчет коэффициента корреляции можно проводить по формуле

Промежуточные вычисления удобно располагать в виде таб­лицы.

Таблица 7

Промежуточные вычисления для расчета коэффициента корреляции

№ наблюдения
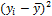
					-4
			-11		-18
			-14		-42
					-4		-28
			-8		-29
			-13		-12
∑

Вычисляем среднее:

Теперь заполняем последние пять столбцов таблицы. Суммируя элементы в соответствующих столбцах, находим

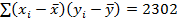
Подставляя вычисленные значения в выражение для r, получаем

Вывод: между весом тела X и весом гребня Y у 15 – дневных петушков существует тесная положительная линейная корреляционная связь.

Коэффициент регрессии B_y/x, определяем по формуле:

Используя данные из таблицы, получим

Подставляя теперь в уравнение прямой регрессии

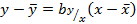
Найденные значения имеем

Последнее уравнение преобразуем к виду

Нанесем исходные данные на координатную плоскость и построим найденную прямую регрессии (рис. 5).

M₁

				X

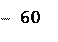Рисунок 5.

Для того, чтобы провести прямую в системе координат, достаточно иметь две точки. У нас одна из них – точка M₁ с координатами . Координаты второй точки M₂

определим, подставив в уравнение регрессии y=0 и вычислив

Отметим, что полученная математическая модель (урав­нение прямой регрессии) обладает прогнозирующими свойст­вами лишь при изменении переменной х от 69 до 95. Так, например, можно с достаточной степенью достоверности счи­тать, что при весе петушка 80 г вес его гребня составит

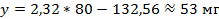
ПРИЛОЖЕНИЯ

Приложение 1

Значение функции

x	Ф(х)	x	Ф(х)	x	Ф(х)	x	Ф(х)	x	Ф(х)	x	Ф(х)
0,00	0,0000	0,50	0,1915	1,00	0,3413	1,50	0,4332	2,00	0,4772	3,00	0,49865
0,01	0,0040	0,51	0,1950	1,01	0,3438	1,51	0,4345	2,02	0,4783	3,20	0,49931
0,02	0,0080	0,52	0,1985	1,02	0,3461	1,52	0,4357	2,04	0,4793	3,40	0,49966
0,03	0,0120	0,53	0,2019	1,03	0,3485	1,53	0,4370	2,06	0,4803	3,60	0,499841
0,04	0,0160	0,54	0,2054	1,04	0,3508	1,54	0,4382	2,08	0,4812	3,80	0,499928
0,05	0,0199	0,55	0,2088	1,05	0,3531	1,55	0,4394	2,10	0,4821	4,00	0,499968
0,06	0,0239	0,56	0,2123	1,06	0,3554	1,56	0,4406	2,12	0,4830	4,50	0,499997
0,07	0,0279	0,57	0,2157	1,07	0,3577	1,57	0,4418	2,14	0,4838	5,00	0,499997
0,08	0,0319	0,58	0,2190	1,08	0,3599	1,58	0,4429	2,16	0,4846
0,09	0,0359	0,59	0,2224	1,09	0,3621	1,59	0,4441	2,18	0,4854
0,10	0,0398	0,60	0,2257	1,10	0,3643	1,60	0,4452	2,20	0,4861
0,11	0,0438	0,61	0,2291	1,11	0,3665	1,61	0,4463	2,22	0,4868
0,12	0,0478	0,62	0,2324	1,12	0,3686	1,62	0,4474	2,24	0,4875
0,13	0,0517	0,63	0,2357	1,13	0,3708	1,63	0,4484	2,26	0,4881
0,14	0,0557	0,64	0,2389	1,14	0,3729	1,64	0,4495	2,28	0,4887
0,15	0,0596	0,65	0,2422	1,15	0,3749	1,65	0,4505	2,30	0,4893
0,16	0,0636	0,66	0,2454	1,16	0,3770	1,66	0,4515	2,32	0,4898
0,17	0,0675	0,67	0,2486	1,17	0,3790	1,67	0,4525	2,34	0,4904
0,18	0,0714	0,68	0,2517	1,18	0,3810	1,68	0,4535	2,36	0,4909
0,19	0,0753	0,69	0,2549	1,19	0,3830	1,69	0,4545	2,38	0,4913
0,20	0,0793	0,70	0,2580	1,20	0,3849	1,70	0,4554	2,40	0,4918
0,21	0,0832	0,71	0,2611	1,21	0,3869	1,71	0,4564	2,42	0,4922
0,22	0,0871	0,72	0,2642	1,22	0,3883	1,72	0,4573	2,44	0,4927
0,23	0,0910	0,73	0,2673	1,23	0,3907	1,73	0,4582	2,46	0,4931
0,24	0,0948	0,74	0,2703	1,24	0,3925	1,74	0,4591	2,48	0,4934
0,25	0,0987	0,75	0,2734	1,25	0,3944	1,75	0,4599	2,50	0,4938
0,26	0,1026	0,76	0,2764	1,26	0,3962	1,76	0,4608	2,52	0,4941
0,27	0,1064	0,77	0,2794	1,27	0,3980	1,77	0,4616	2,54	0,4945
0,28	0,1103	0,78	0,2823	1,28	0,3997	1,78	0,4625	2,56	0,4948
0,29	0,1141	0,79	0,2852	1,29	0,4015	1,79	0,4633	2,58	0,4951
0,30	0,1179	0,80	0,2881	1,30	0,4032	1,80	0,4641	2,60	0,4953
0,31	0,1217	0,81	0,2910	1,31	0,4049	1,81	0,4649	2,62	0,4956
0,32	0,1255	0,82	0,2939	1,32	0,4066	1,82	0,4656	2,64	0,4959
0,33	0,1293	0,83	0,2967	1,33	0,4082	1,83	0,4664	2,66	0,4961
0,34	0,1331	0,84	0,2995	1,34	0,4099	1,84	0,4671	2,68	0,4963
0,35	0,1368	0,85	0,3023	1,35	0,4115	1,85	0,4678	2,70	0,4965
0,36	0,1406	0,86	0,3051	1,36	0,4131	1,86	0,4686	2,72	0,4967
0,37	0,1443	0,87	0,3078	1,37	0,4147	1,87	0,4693	2,74	0,4969
0,38	0,1480	0,88	0,3106	1,38	0,4162	1,88	0,4699	2,76	0,4971
0,39	0,1517	0,89	0,3133	1,39	0,4177	1,89	0,4706	2,78	0,4973
0,40	0,1554	0,90	0,3159	1,40	0,4192	1,90	0,4713	2,80	0,4974
0,41	0,1591	0,91	0,3186	1,41	0,4207	1,91	0,4719	2,82	0,4976
0,42	0,1628	0,92	0,3212	1,42	0,4222	1,92	0,4726	2,84	0,4977
0,43	0,1664	0,93	0,3238	1,43	0,4236	1,93	0,4732	2,86	0,4979
0,44	0,1700	0,94	0,3264	1,44	0,4251	1,94	0,4738	2,88	0,4980
0,45	0,1736	0,95	0,3289	1,45	0,4265	1,95	0,4744	2,90	0,4981
0,46	0,1772	0,96	0,3315	1,46	0,4279	1,96	0,4750	2,92	0,4982
0,47	0,1808	0,97	0,3340	1,47	0,4292	1,97	0,4756	2,94	0,4984
0,48	0,1844	0,98	0,3365	1,48	0,4306	1,98	0,4761	2,96	0,4985
0,49	0,1879	0,99	0,3389	1,49	0,4319	1,99	0,4767	2,98	0,4986

Приложение 2

Таблица значений

n		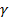n	γ
0.95	0.99	0.999	0.95	0.99	0.999
	2,78	4,60	8,61		2,093	2,861	3,888
	2,57	4,03	6,86		2,064	2,797	3,745
	2,45	3,71	5,96		2,045	2,756	3,659
	2,37	3,50	5,41		2,032	2,720	3,600
	2,31	3,36	5,04		2,023	2,708	3,558
	2,26	3,25	4,78		2,016	2,692	3,527
	2,23	3,17	4,59		2,009	2,679	3,502
	2,20	3,11	4,44		2,001	2,662	3,464
	2,18	3,06	4,32		1,996	2,649	3,439
	2,16	3,01	4,22		1,991	2,640	3,418
	2,15	2,98	4,14		1,987	2,633	3,403
	2,13	2,95	4,07		1,984	2,627	3,392
	2,12	2,92	4,02		1,980	2,617	3,374
	2,11	2,90	3,97		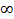1,960	2,576	3,291
	2,10	2,88	3,92

Дата добавления: 2014-10-15