Решение типовой задачи. В ЗАДАЧАХ 71—80 заданы результаты обследования

ЗАДАЧИ КОНТРОЛЬНОЙ РАБОТЫ

В ЗАДАЧАХ 71—80 заданы результаты обследования.

Требуется: 1) получить вариацион­ный ряд и построить гистограмму относительных частот; 2) вычислить выборочную среднюю 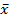, дисперсию s², среднее квадратическое отклоне­ние s, коэффициент вариации V, ошиб­ку средней ; 3) с надежностью 95% указать доверительный интер­вал для оценки генеральной средней.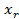

Обследовано по весу (кг) 20 кроликов. Результаты обсле­дования представлены в табл. 1.

Таблица 1

№ наблюдения	№ задачи
	3,1	5,5	3,2	6,0	4,8
	4,2	5,9	3,8	4,5	5,4
	5,0	7,5	4,1	4,7	4,9
	4,6	5,4	4,3	5,7	3,8
	6,4	3,4	4,3	5,2	5,5
	5,3	5,2	5,6	3,8	5,2
	3,8	4,3	6,0	4,3	6,4
	5,1	4,7	5,7	4,3	6,7
	4,9	5,8	4,5	5,1	5,8
	5,4	6,8	5,0	5,7	5,4
	5,9	4,0	6,7	6,3	4,7
	6,5	5,7	5,3	4,8	3,3
	5,5	4,5	5,4	5,6	5,1
	5,7	5,3	4,7	6,4	4,6
	4,7	6,3	4,3	7,2	5,8
	5,6	5,2	5,9	5,0	6,0
	5,8	4,1	6,5	5,3	7,1
	7,3	5,1	7,1	5,1	5,2
	4,7	5,0	3,4	4,2	5,5
	5,5	6,2	4,6	3,7	4,7

Обследовано 20 телят холмогорских помесей. Их живая масса при рождении (кг) представлена в табл. 2.

Таблица 2

№ наблюдения	№ задачи

Задач а. Из крупного стада коров произведена случайная выборка, получено 20 вариант удоя коров за 300 дней лактации (в ц): 35,9; 35,3; 42,7; 45,2; 25,9; 35,3; 33,4; 27,0; 35,9; 38,8; 33,7; 38,6; 40,9; 35,5; 44,1; 37,4; 34,2; 30,8; 38,4; 31,3.

Требуется:

1) получить вариационный ряд и построить гистограмму относительных частот;

2) найти основные выборочные характеристики: .

3) С надёжностью 95% указать доверительный интервал для оценки генеральной средней .

Решение.

1) Запишем исходные данные в виде ранжированногт ряда, т. е. располагая их в порядке возрастания:

25,9; 27,0; 30,8; 31,3; 33,4; 33,7; 34,2; 35,3; 35,3; 35,5; 35,9; 35,9; 37,4; 38,4; 38,6; 38,8; 40,9; 42,7; 44,1; 46,2.

Максимальное значение признака составляет 46,2 ц, а минимальное - 25,9 ц. разница между ними составляет 20,3 ц. Этот интервал надо разбить на определенное количество классов. При малом объеме выборки (20-40 вариант) намечают 5 – 6 классов. Возьмем длин классового интервала 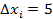. Получаем пять интервалов: первый 25 – 30, второй 30 – 35, третий 35 – 40, четвертый 40 – 45, пятый 45 – 50 (начало первого класса не обязательно должно совпадать со значением минимальной варианты).

С помощью ранжированного ряда определим частоту попадания вариант выборки в каждый интервал. В первый интервал попадает два значения (25,9 и 27,0), поэтому 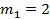. Во второй интервал попадают пять значений (проверьте!), поэтому 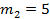. Аналогично .

Теперь найдем относительные частоты попадания вариант выборки в каждый интервал:

в первый интервал;

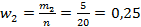во второй интервал;

в третий интервал;

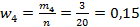в четвертый интервал;

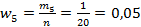в пятый интервал.

Для проверки вычисляем сумму относительных частот:

Тот факт, что в сумме получили единицу, подтверждает правильность вычислений.

По формуле:

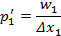
Вычислим плотности P₁ относительных частот вариант. Получаем

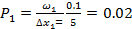для первого интервала

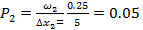для второго интервала

для третьего интервала

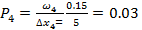для четвертого интервала

для пятого интервала

Полученные результаты сведем в таблицу.

Таблица 3.

Интервал значений удоя (ц)	25-30	30-35	35-40	40-45	45-50
Частоты вариант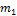
Относительные частоты	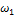0.10	0.25	0.45	0.15	0.05
Плотность относительных частот P1	0.02	0.05	0.09	0.03	0.01

Рисунок 4.

Строим гистограмму относительных частот — ступенча­тую фигуру, состоящую из прямоугольников, основаниями которых являются классовые интервалы, а высотами — со­ответствующие значения плотностей относительных частот P₁. Классовые интервалы изображают на оси абсцисс, а значения Р₁ откладывают на оси ординат.

Для нашего примера гистограмма относительных частот изображена на рис. 4.

2) Основные выборочные характеристики вычисляются по формулам:

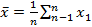- выборочная средняя;

– дисперсия;

– среднее квадратическое отклонение;

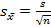– ошибка средней;

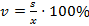- коэффициент вариации.

Расчеты 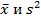удобно проводить с помощью таблицы.

Таблица 4

№ п/п	Результат обследования,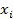
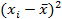
	35,9	-0,1	0,01
	35,3	-0,7	0,49
	42,7	6,7	44,89
	45,2	9,2	84,64
	25,9	-10,1	102,01
	35,3	-0,7	0,40
	33,4	-2,6	6,76
	27,0	-9,0	81,00
	35,9	-0,1	0,01
	38,8	2,8	7,84
	33,7	-2,3	5,29
	38,6	2,6	6,76
	40,9	4,9	24,01
	35,5	-0,5	0,25
	44,1	8,1	65,61
	37,4	1,4	1,86
	34,2	-1,8	3,24
	30,8	-5,2	27,04
	38,4	2,4	5,76
	31,3	-4,7	22,09
∑	720,3		490,05

Просуммировав варианты 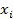, занесем сумму ∑ 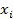в нижнюю строку таблицы под соответствующим столбцом. Разделив эту суму на 20 получим

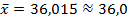
Теперь заполняем следующий столбец таблицы, в кото­рый записываем разности Для контроля можно вычис­лить сумму всех таких разностей. Если разности вычислены правильно, то их сумма равна нулю.

Затем возводим эти разности в квадрат и заполняем по­следний столбец таблицы. Вычислив сумму 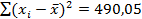и разделив ее на n-1=20-1=19, получим значе­ние дисперсии

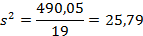
Извлекая с помощью таблиц или микрокалькулятора квадратный корень из величины , находим

S= 5,08

Затем ошибку средней:

Вычисляем коэффициент вариации

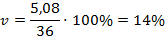
Поскольку 10%<V<20%, то изменчивость удоев за 300 дней следует считать средней.

3) Доверительный интервал для оценки генеральной средней определяется как:

Где величина 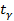при заданной надежности 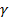определяется с помощью таблиц приложения 2. В нашем примере

Вычисляем теперь радиус доверительного интервала:

Таким образом, с надежностью 95% можно утверждать, что во всем стаде средний удой за 300 дней (генеральная средняя) заключен в пределах от 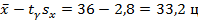(гарантированный минимум) до 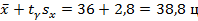(возможный максимум).

Дата добавления: 2014-10-15