Задачи контрольной работы. Вопросы для самопроверки

Вопросы для самопроверки

1. Дайте определение дифференциального уравнения пер­вого порядка.

2. Что называется решением дифференциального уравнения? Общим решением? Частным решением?

3. Какова роль начальных условий при решении дифференциального уравнения?

4. Какие уравнения называются дифференциальными уравнения с разделяющимися переменными?

5. Приведите примеры задач биологического или технического содержания, сводящиеся к дифференциальным уравнениям с разделяющимися переменными?

6. Какова методика отыскания решения дифференциального уравнения с разделяющимися переменными?

7. Какие уравнения называются линейными дифференциальными уравнениями первого порядка? Каковы методы их решения?

В ЗАДАЧАХ 51—60 требуется составить дифференциаль­ное уравнение динамики развития некоторого биологического вида и найти решение этого уравнения.

Состояние популяции (в простейшем понимании — ста­да) можно охарактеризовать массой m этой популяций (т. е. весом всего стада), причем масса m является функци­ей времени m=m(t). Считая, что скорость прироста биомас­сы пропорциональна биомассе популяции с коэффициентом k = k(t) и что известна начальная биомасса (при t=0), найти величину биомассы в момент t = T.

51.
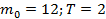
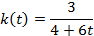
52.
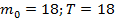
53.
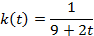
54.
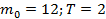
55.
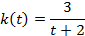
56.
57.
58.
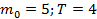
59.
60.

Дата добавления: 2014-10-15