Позиционные звенья

Типовые звенья линейных систем и их динамические характеристики

Типовым элементарным динамическим звеном называется звено, динамика которого описывается диффернциальным уравнением не выше второго порядка.

Типовые звенья классифицируются в зависимости от вида дифференциального уравнения на позиционные, интегрирующие, дифференцирующие, запаздывания.

Позиционными называются звенья в левой части дифференциального уравнения которых выходная величина и её производные, а в правой – входная величина.

1) Усилительное звено:

уравнение звена имеет вид у(t)=kx(t) (1)

передаточная функция звена: W(p)=y(p)/x(p)=k;

переходная функция: h(t)=L^-1{W(p)/p}=L^-1{k/p}=k∙1(t).

Весовая функция представляет собой импульс, площадь которого равна к, т.е. при x(t)=δ(t); y(t)=ω(t)=k∙ δ(t)

Получим частотные характеристики усилительного звена.КЧХ:

W(jω)=k

AЧХ: А(ω)=к; ФЧХ: φ(ω)=0 на всех частотах.

Рис 9.1 Динамические и частотные характеристики усилительного звена

2) Апериодическое звено I-го порядка

Звено, в котором при скачкообразном изменении входной величины выходная величина апериодически (по экспоненте) стремится к новому установившемуся значению, называется апериодическим (инерционным).

Пример (рис. 9.2):

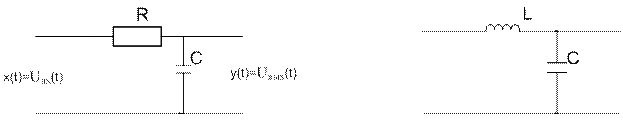
Рис. 9.2. Примеры инерционных звеньев

Дифференциальное уравнение звена имеет вид:

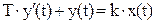(1)

где Т – постоянная времени [c],

k – коэффициент передачи.

Операторное уравнение звена:

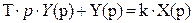
Тогда передаточная функция звена:

.

Переходная функция звена:

Весовая функция звена:

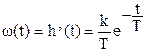
Рис 9.3 Временные характеристики инерционного звена

Постоянная времени Т представляет собой интервал времени, в течение которого выходная величина достигла бы своего нового установившегося значения, если бы она изменялась с постоянной скоростью, равной скорости её изменения в начальный момент времени после поступления на вход единичного входного сигнала.

Чем >Т тем медленнее переходный процесс. Теоретически, переходный процесс в апериодическом звене длится бесконечно долго.

Под временем переходного процесса понимают промежуток времени, по истечении которого входная величина достигнет 0,95 от установившегося значения.

При t=3T

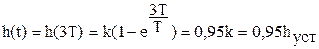, т.е .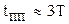

При t=T

Т можно определить как время, за которое входная величина изменяясь от 0 достигла 0,63 от установившегося значения, при подаче на вход звена единичного ступенчатого воздействия.

Для весовой функции при t=T:

.

Получим частотные характеристики звена.

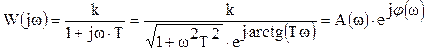
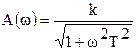КЧХ:

- АЧХ

- ФЧХ

В §.8. определяли ВЧХ и МЧХ:

;

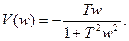
Построим асимптотическую ЛАХ звена:

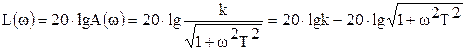(2)

Для построения уравнения асимптот рассмотрим следующие интервалы частот:

1. При малых частотах

ωT<<1 или ω<<(1/Т),1/Т – частота сопряжения. Пренебрегаем величиной 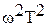в (2), тогда уравнение первой асимптоты имеет вид:

(0 дб/дек)

2. При частотах ω>>(1/Т) пренебрегаем 1 в (2), тогда получим уравнение второй асимптоты:

(-20 дб/дек)

Рис. 9.5. Асимптотическая ЛАХ звена

Если построить действительную ЛАХ по уравнению (2), то наибольшая погрешность будет на частоте . Определим ΔL(ω):

дБ.

Дата добавления: 2014-10-15