Первоначальное изучение граничного поведения

Ядро Пуассона Р_r(θ) обладает и четвертым свойством:

d) Для любого σ > О, Р_r(θ) →0 равномерно для σ≤│θ│≤π при r→1.

Это сразу следует из формулы для Р_r(θ).

Теорема. Пусть функция F непрерывна на R и F(t+2π)=F(θ). Пусть

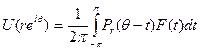
Тогда U(z)→F(φ), когда , и сходимость равномерна по φ.

Доказательство.

Этот результат восходит к самому Пуассону, который полагал, что отсюда вытекает сходимость ряда Фурье функции к ней самой (на самом деле из теоремы это не следует!). Запишем

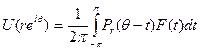
Для заданного произвольного числа <р мы имеем по свойству с)

Следовательно,

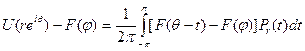
Пусть таково, что |F(s)— F(φ)| < ε при |s — φ|<2ϭ;

число ϭ здесь зависит только от ε, а не от φ, из-за (равномерной!) непрерывности функции F.

Запишем интеграл в правой части в виде суммы двух:

Если |θ-φ|< ϭ то первый интеграл справа не превосходит

Tb М — верхняя грань величины | F(t)|. Тогда второй интеграл не превосходит

,

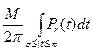что меньше ε, если r достаточно близко к 1, в силу свойства d).

Таким образом, 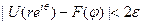, если |θ-φ|< ϭ, а r достаточно близко к 1.

Q. E. D.

Замечание. Свойства a), b), с) и d) вместе взятые показывают, что представляет собою так называемую аппроксимативную единицу. Доказанная теорема имеет место в силу этих свойств: не только для ядра Пуассона, но и для других ядер, являющихся аппроксимативными единицами, справедливы аналогичные результаты.

Теорема. Пусть пусть функция F[t) непре­рывна в точке θ₀. Тогда 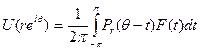стремится к F(θ₀) при стремлении re^iθ к e^iθ

Доказательство такое же, как у предыдущей теоремы.

Теорема. Пусть , 1≤ р < ∞, и пусть

.

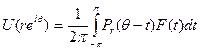Тогда 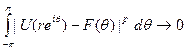, т.е. стремится к F(G) в А"-норме при r → 1.

Доказательство.

Положим F_r(θ) = U(re^1θ). Тогда

Используя свойства а) и с) (мы рассматриваем 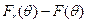как предел выпуклых комбинаций функций . считая t параметром, а θ — переменной), имеем по очевидному обобщению неравенства треугольника

.

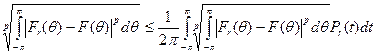Полагая

получим

Но при 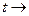0. Это так, потому что сдвиг непрерывен в L^P-норме для 1≤р <∞. Это следует в свою очередь из элементарных фактов теории функций вещественной переменной. Действительно, пусть даны ) и ε > 0. Найдем непрерывную функцию G, периодическую с периодом 2π, такую что ||F — G||_p<ɛ. Тогда, очевидно,

для | t|<ϭ при достаточно малых σ в силу равномерной непрерывности; следовательно,

для |t|<σ.

Во всяком случае, функция Ф(t) непрерывна в 0, где она равна нулю.

Поэтому, по предыдущей теореме, 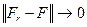при r→∞. Q. E. D.

При р = ∞ все, что мы имеем, — это ω*-сходимость:

Теорема. Если и

,

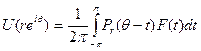то при r →1

Доказательство.

Возьмём произвольную функцию Нужно доказать, что

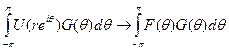
при r →1. Но это так, потому что (используем чётность ) стремится к G(t) при r →1 по предыдущей теореме. Остаётся только применить теорему Фубини.

Аналогично справедлива

Теорема. Пусть где μ — конечная вещественная мера на [-π,π]. Тогда 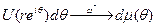при r →1, т. е. для любой непрерывной функции G (θ), периодической с периодом 2π,

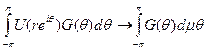
когда r →1

Доказательство.

Применяем теорему Фубини вместе с первым результатом этого подпункта.

Дата добавления: 2014-10-15