Бесконечные числовые произведения комплексных чисел и их сходимость

Лекция 9

Бесконечное произведение есть выражение вида

(1+а₁)(1+а₂)(1+а₃).... (1)

содержащее бесконечно много сомножителей. Мы обозначаем его через

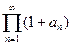
Мы предполагаем, что ни одно из чисел а„ не равно —1. Рассмотрим частичное произведение

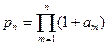
Мы говорим, что бесконечное произведение (1) сходится, если р_n стремится к некоторому пределу, отличному от нуля, когда п →∞

Мы могли бы, конечно, допустить предел 0, как всякий другой; но мы увидим ниже, что во многих случаях это было бы неудобно.

Если произведение не сходится, то говорят, что оно расхо­дится. Если 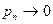, то говорят, что оно расходится к нулю.

Мы начнем с рассмотрения двух простых случаев.

Если a_n,≥0 то произведение П(1+a_n) и ряд 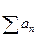сходятся или расходятся одновременно.

Так как в этом случае р_n есть неубывающая функция от п, то р_n стремится либо к конечному пределу, либо к положительной бесконечности. Далее,

Левое неравенство становится очевидным, если раскрыть скобки; правое неравенство следует из того, что 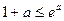при любом положительном а. Вместе эти неравенства показывают, что р_n и a₁ +…+a_n ограничены или не ограничены одновременно, и это завершает доказательство.

Если a_n,≤0 для всех значений п, то мы полагаем a_n = -b_n и рассматриваем произведение

Если для всех значений п и ряд сходится, то произведение П(1 — b _п) сходится.

Из сходимости ряда следует существование столь большого N, что b_N + b_N+1+…<1/2 и, в частности, b_n < 1 при n≥N. Оче­видно,

(1 - b_N) (1 - b_N+1)≥1- b_N - b_N+1,

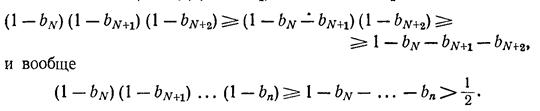
Таким образом, отношение р_п/p_N+1 монотонно убывает при п> N и имеет положительную нижнюю грань. Следовательно, оно стре­мится к положительному пределу. Поскольку , это завер­шает доказательство.

Если 0≤b_n для всех п, но ряд расходится, то про­изведение П(1 — b_n) расходится к нулю.

В самом деле, 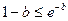, если 0≤b<1, так что

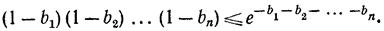
Правая часть стремится к нулю, что и завершает доказательство.

Таким образом, если если 0≤b_n<1, то произведение П(1 — b_n) и ряд сходятся или расходятся одновременно.

Общий случай. Пусть теперь a_n — любые вещест­венные или комплексные числа, отличные от —1.

Определение. Произведение П(1+a_n) называется абсолютно сходящимся, если произведение П(1 — |a_n |) сходится.

Из первого предложения следует, что необходимым и достаточным условием абсолютной сходимости произведения П(1+a_n) служит сходимость ряда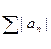

Покажем теперь, что абсолютно сходящееся произведение схо­дится.

Обозначим через р_п то же частичное произведение, что и выше,

и положим 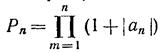Так как

то |р_п — p _n-1|≤|Р_п — Р_п-1|- Если произведение П(1 +|a_n|) схо­дится, то Р„ стремится к некоторому пределу, так что ряд сходится. Тогда, в силу теоремы сравнения, схо­дится и ряд 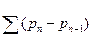стремится к некоторому пре­делу.

Этот предел не может быть нулем. Действительно, так как ряд 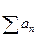сходится и 1+а_п→1, то ряд

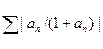
также сходится. Следовательно (в силу только что доказанного), произведение

стремится к некоторому пределу.

Но это произведение равно 1/р_п- Следовательно, предел произ­ведения р_п отличен от нуля.

Дата добавления: 2014-10-15