Логарифм бесконечного произведения

Пусть

верно ли, что

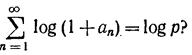Здесь log z главное значение логарифма числа z, т. е. значение, мнимая часть которого лежит между —π и π

Ответ будет, очевидно, утвердительным, если все числа а_п действительны и положительны, поскольку тогда все логарифмы имеют свое обычное арифметическое значение. Но в общем случае формула требует модификации.

Пусть р_п обозначает п-е частичное произведение, и пусть , так что р_п и ρ_n стремятся к пределам и то же отно­сится к аргументу φ_n, если его значения выбраны надлежащим образом. Пусть

тогда, так как а_л →0 при n→∞, то и θ_n →0 Положим

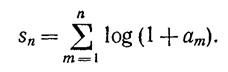
Очевидно,

где k_n — целое число, и 2k_nπ = θ₁ +…+ θ₂ – φ_n. так что

Поскольку правая часть стремится к нулю, при достаточно большом n

и, следовательно, k_n+1 = k_n (напомним, что все k_n — целые числа). Таким образом, k_n имеет при достаточно большом п постоянное значение, скажем k, т. е. Следова­тельно,

Сумма ряда есть, таким образом, некоторое значение, но не обязательно главное значение, логарифма произведения.

Заметим, что в ходе доказательства мы получили для всех достаточно больших значений N равенство

Если мы начнем с ряда логарифмов и положим

то после перехода к экспоненциалам в формуле (1), мы получим равенства

Равномерная сходимость бесконечных произведений.

Бесконечное произведение

где сомножители — функции переменного z, вещественного или комплексного, называется равномерно сходящимся в некоторой области значений z, если частичное произведение

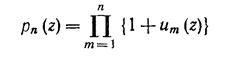
равномерно сходится в этой области к некоторому пределу, нигде не равному нулю.

Вот простейший признак равномерной сходимости произведения.

Произведение

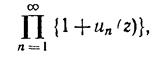
равномерно сходится в каждой области, в которой ряд 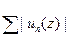равномерно сходится к ограни­ченной функции.

Доказательство состоит в пересмотре аргументов ранее доказанной теоремы с точки зрения равномерности. Пусть М — верхняя грань суммы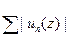

в рассматриваемой области. Тогда

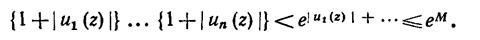
Полагая

мы видим, что

Следовательно, ряд равномерно сходится, и доказательство завершается так же, как в прошлый раз

Дата добавления: 2014-10-15