Ряд Тэйлора конформного отображении абсолютно сходится вплоть до границы

Б о

Образы множеств меры нуль на единичной окружности

Если А — дуга кривой Г, то Ф взаимно-однозначно отображает некоторую дугу j окружности {|z|=1} на Ʌ. Само определение длины дуги теперь нам дает

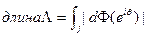
Теорема (Ф. и М.. Риссы). Если. j — дуга единичной окружности и 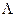= Ф(j),то

Доказательство.

По теореме предыдущего подпункта 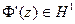, поэтому

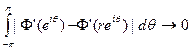при r→1

Пусть Т(θ) — непрерывно дифференцируемая 2π-периидичеекая функция. Интегрируя по частям, находим

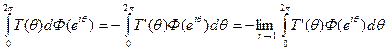
Но при любом r < 1

Правая часть этого равенства по замечанию, желанному вначале, стремится к Итак,

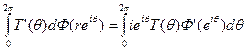
какова бы ни была 2π-периодическая непрерывно дифферен­цируемая функция Т. Пусть теперь 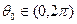, а — рав­номерно ограниченная последовательность таких функций, сходящаяся к единице в (0,θ₀) и к нулю в [0, 2π] \(0,θ₀). Подставляя Т_п вместо Т в последнее равенство и переходя к пределу, по теореме Лебега получаем

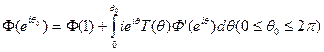
Следовательно,

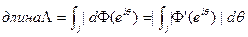
Теорема доказана,

Длина дуги кривой Г может быть очевидным образом использована для определения линейной меры на Г. Сначалапусть Ơ— (относительно) открытое подмножество Г тогда Ơ есть счётное объединение попарно Heпepeceкающихся открытых дуг Ʌ_k, и мы положим |Ơ|=длина Ʌ _k. Для произвольного подмножества 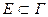определим |E| какinf { |Ơ|: Ơ , Ơоткрыто в Г}. Так как Ф — гомеоморфное отображение окружности {|z|= 1} на Г, то легко показать, основываясь на вышеприведенной теореме, что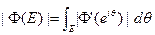

борелевсках множеств Е на единичной окружности. Имеет место следующий важный результат:

Теорема (Ф. и М. Риссы). Если Е - подмножество единичной окружности и {|z|= 1}, то |Ф(Е)| = 0.

Доказательство.

Пусть — открытые множества на {|z|= 1}, такие что 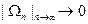Тогда |Ф(Е)|≤|Ф(Ω_п) | для всех n. Но из предыдущей тео­ремы н следующего за ней обсуждения вытекает, что

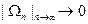этот интеграл стремится к нулю при так как и .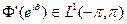

Теорема (Харди). Степенной ряд функции Ф(z) абсолютно сходится вплоть до {|z|= 1}.

Дoказательство.

По подпункту 1° имеем 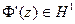. Кроме того, поскольку отображение Ф конформно, то Ф'(z) не обращается в нуль в {|z|<1}. Следовательно, мы можем определить аналитическую в {|z|<1} функцию 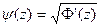Теперь, для |z| < 1 запишем

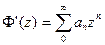
Тогда

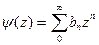
где

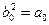
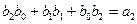
и т.д.

Так как 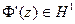, то средние

ограничены при r < 1. По равенству Парсеваля отсюда следует, что

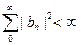
Теперь положим

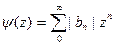
Используя равенство Парсеваля, получаем, что средние

ограничены при r < 1.

Пусть θ(z) = [ψ(z)]² разлагается, скажем, в степенной ряд Тогда, с одной стороны, , а с другой —

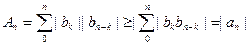
Имеем

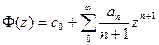
так что для доказательства абсолютной сходимости степен­ного ряда функции Ф(z) вплоть до {| z |= 1} нам надо показать, что

Для |z|< 1, взяв главную ветвь логарифма, получаем

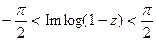
и

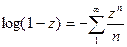
так что

для z = rе^iθ, 0< r <1; умножая на 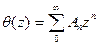и используя абсолютную сходимость и ортогональность находим что

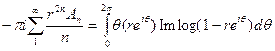
это по абсолютной величине не превосходит 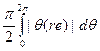, что равномерно по r< 1 ограничено, скажем, константой М. Поскольку А_n ≥ 0, то мы получаем, устремляя r к I, что

, как и требовалось.

Дата добавления: 2014-10-15