Области, ограниченные спрямляемой жордановои кривой

Лекция 9 - 12

Приложения неравенства Фейера-Рисса в комплексном анализе. Изучение свойств конформно отображающих функций.

Рассмотрим теперь область, G ограниченную спрямляемой жордановой кривой.

Пусть Ф— конформное отображение единичного круга на G — область, ограниченную жордановой спрямляемой кривой Г

По теореме Каратеодори Ф обладает непрерывным взаимно-однозначным продолжением вплоть до { |r |= 1} и отображает эту окружность на Г. По­этому ясно, что если [e^iθ0, e^iθ1,,…, e^iθp] — разбиение окруж­ности {| r | = 1}, то [Ф(e^iθ0), Ф(e^iθ1,),…, Ф(e^iθp)] — разбиение кривой Г.

1° Производная конформного отображения принадлежит классу Н¹

Теорема .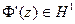

Доказательство

Пусть ε= e^2πi/n. Тогда функция

является субгармонической в {| r |<1}; она непрерывна для |z|<1 в силу непрерывности Ф(z). Поэтому, по принципу максимума, при |z|<1

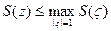
Нo если |ζ|= 1то точки

[Ф(ζ), Ф(ε^п ζ ),…, Ф(ε^пζ)]

образуют разбиение кривой Г; следовательно, по определению длины кривой

S(ζ)≤длина Г. Теперь зафиксируем r<1. Мы имеем

Итак, если |z|<1, то S(z)<длина Г. Теперь зафиксируем r < 1. Мы имеем

длины Г< ∞.

Устремляя n к бесконечности и используя непрерывность функции Ф'(r е'^е) по θ для r< 1, получаем в пределе

длины Г

поскольку это выполняется для всех r<.1, то

Дата добавления: 2014-10-15