Единице. Граничные значения почти всюду равны по модулю

Граничные значения почти всюду равны по модулю

Бесконечные функциональные произведения, равномерная сходимость. Бесконечные произведения Бляшке

Лекция 10

А. Произведение Бляшке

Если 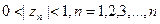.., и бесконечное произведение

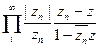
сходится для | z |< 1, то оно представляет некоторуюфунк­цию, аналитическую в единичном круге; она называется про­изведением Бляшке. Можно даже допустить равенство конечного числа чисел z_n нулю - просто в этом случае множители, соответствующие 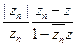заменяются на z.

Имеем

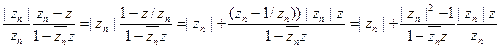
откуда

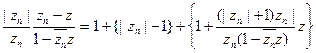
следовательно, рассматриваемое бесконечное произведение сходится при z = 0 тогда в только тогда, когда

Но если , то по той же только что най­денной формуле

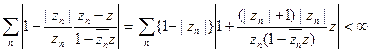
при | z |<1; поэтому бесконечное произведение сходится в { \z\ < 1}, если . Таким образом,

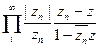сходится в {|z|<1} тогда и только тогда, когда .

Пусть так что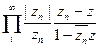

сходится в {| z |< 1} и представляет функцию В(z), аналитиче скую в этом круге. Согласно элементарной теории функции комплексной переменной, из того, что каждый сомножитель произведения по модулю меньше 1 в {|z|< 1}, вытекает, что \В(z)\< 1 для |z\< 1.

Следовательно, для почти всех ζ, |ζ|=1, предельная функция B(ζ)=limB(z) при z →ζсуществует (теарема Фату).

Теорема. |В(е^iθ)|=1 п. в.

Доказательство.

Без ограничения общности можно счи­тать, что все точки z_n отличны от нуля (в противном случае мы рассмотрели бы функцию B(z)/z^k вместо В (z)). Тогда 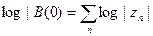Теперь из того, что вытекает, что 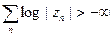. (NB: 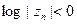для каждого п. Возьмём число r, 0< r < 1, не равное ни одной из величин |z_n |. Тогда в силу простейшей разновидности фор­мулы Йенсена

,

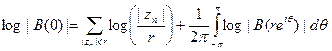т. е.

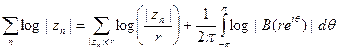
или

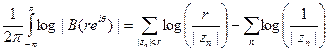
Выберем и зафиксируем какое-нибудь число р, такое что 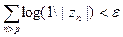, и возьмём r < 1 настолько блнзким к 1, чтобы при п= 1,2,,.., р все точки z_n лежали в круге {\z\<r}. Тогда из предыдущего соотношения получим

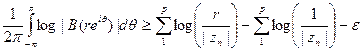
или, если взять r < 1 достаточно близким к 1,

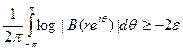
Это значит, что

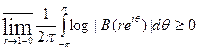
поскольку число ɛ>0 было произвольным. Но В (re^iθ) →В (е^iθ) п. в. при r →1, и

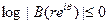
Следовательно, по лемме Фату (переходим к пределу по последовательности чисел r, стремящихся к 1)

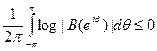
Поскольку 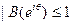, мы получаем, что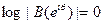

Дата добавления: 2014-10-15