Прочность и вязкость дисперсных систем

Свободнодисперсные жидкообразные системы обладают вязкостью и способны течь. Вязкие тела текут при любом напряжении сдвига P_τ, которое выражается уравнением

P_τ= F/B, (11.4)

где F — сила вязкого сопротивления; В — площадь, на которую распространяется действие этой силы.

Течение вязких тел определяется законом Ньютона:

(11.5)

где η — коэффициент вязкости; dy/dt — изменение деформации во времени (скорость деформации).

Если обозначить скорость деформации через g, то в соответствии с формулой (11.5) вязкость системы равна

η = P_τ/. (11.6)

Вязкость свободнодисперсных систем растет по мере увеличения концентрации дисперсной фазы. Присутствие частиц дисперсной фазы приводит к искажению потока жидкости вблизи этих частиц, что влияет на вязкость дисперсной системы. Если концентрация незначительна, то столкновение частиц исключается, и характер движения жидкости около одной из частиц повлияет на движение жидкости вблизи других. В этих условиях для определения вязкости свободнодисперсных систем можно воспользоваться формулой Эйнштейна

η = η₀(1 + к v _об); η/η₀= 1 + к v _об, (11.7)

где η, η₀— коэффициент вязкости свободнодисперсной системы и дисперсионной среды; к — коэффициент, зависящий от формы частиц, для сферических частиц к = 2,5; v _об— объемная концентрация дисперсной фазы, определяемая по формуле (1.10).

В соответствии с формулой (11.7) вязкость свободнодисперсной системы увеличивается по мере роста объемной концентрации частиц дисперсной фазы. Вязкость золя коллоидов диффузионного сока при производстве сахара в зависимости от массовой концентрации изменяется следующим образом:

Массовая концентрация, 10–2г/м³, 0,54 1,31 1,62

Вязкость, 10³Па∙с 1,109 1,291 1,150

При увеличении массовой концентрации примерно в 1,5 раза вязкость увеличивается всего в 0,4 раза.

Согласно формуле Эйнштейна вязкость раствора не зависит от размеров частиц сферической формы, если они меньше размеров прибора, определяющего вязкость, и намного больше размеров молекул дисперсионной среды. Впоследствии была показана справедливость этой формулы для частиц, имеющих форму эллипсоида, диска, гантели и других трехмерных частиц; для таких частиц изменяется лишь численное значение коэффициента к.

Формула Эйнштейна справедлива при отсутствии деформации частиц, если концентрация дисперсной фазы не превышает 6%.

При увеличении объемной концентрации сферических частиц до 30% в условиях взаимного столкновения частиц для определения вязкости можно воспользоваться следующей формулой:

η = η₀(1 + 2,5 v об+ 14,7 v ²_об). (11.8)

Эта формула отличается от формулы Эйнштейна последним членом.

Существует ряд других формул, позволяющих с достаточной степенью точности определить вязкость свободнодисперсных систем в зависимости от концентрации и формы частиц дисперсной фазы.

При сопоставлении формул (11.7) и (11.8) видно, что по мере увеличения концентрации дисперсной фазы линейная зависимость между вязкостью и концентрацией нарушается. Тем не менее, вязкость подобных систем при данной концентрации остается постоянной. Подобные системы называют ньютоновскими (в отличие от неньютоновских).

Течение и вязкость неньютоновских жидкостей, которые называют еще аномальными жидкостями, зависят от внешнего воздействия (напряжения сдвига). Вязкость является величиной переменной для данной концентрации и уже не определяется соотношением (11.5) или (11.6).

Рассмотрим особенности движения структурированных твердообразных систем (рис. 11.5). На этом рисунке показана зависимость вязкости и скорости движения (или скорости деформации) от внешнего напряжения.

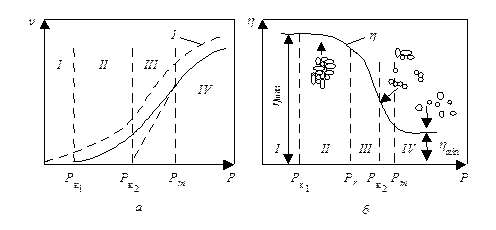
Рис. 11.5. Зависимость скорости течения v (а) и коэффициента вязкости h (б) от внешнего усилия Р:

Р _r— предел прочности; Р _к1— предел упругости; Р _к2— условный (бингамовский) предел прочности; Р _m— напряжение, соответствующее полному разрушению структуры; h_max— наибольшая вязкость практически неразрушенной структуры; h_min— наименьшая вязкость предельно разрушенной структуры; 1 — для жидкообразных тел

Кривые η = f (P) (см. рис. 11.5, б), называют полными реологическими кривыми течения структурированных дисперсных систем. Каждое значение вязкости на этих кривых соответствует равновесному состоянию этих систем (в том числе в случае их разрушения) в стационарном ламинарном потоке.

Возможны четыре состояния структурированных дисперсныхсистем, соответствующие четырем участкам кривых, изображенных на рис. 11.5. Участок I соответствует условию 0 < Р < Р_к1(Р_к1— предел упругости). В этом состоянии течение отсутствует, и внешнее воздействие не может нарушить прочность системы. При дальнейшем увеличении напряжения, когда Р > Р_к1, система начинает течь (участок II). Скорость перемещения в этом случае незначительна, связи между частицами после их разрушения успевают вновь восстановиться. Структура не разрушается, наблюдается лишь перемещение частиц относительно друг друга. Подобное перемещение называют ползучестью. Вязкость системы в условиях ползучести будет наибольшая, практически она будет соответствовать вязкости неразрушенной структуры.

Так, для конфетной массы типа «Батончики» при давлении 105Па (1 атм) и температуре 301 К вязкость равна 800 Па∙с, т.е. она в 8∙105раз превышает вязкость воды.

Скорость движения системы в условиях ползучести определяется по формуле

v = кP/η, (11.9)

где к — коэффициент, характеризующий структурные особенности дисперсной системы.

Третье состояние дисперсной системы характеризуется процессом разрушения структуры при напряжении, равном пределу прочности Р_r. Необратимое разрушение структуры начинается на границе участков II и III, а на границе участков III и IV оно заканчивается. В этом состоянии дисперсной системы связи между частицами не восстанавливаются, вязкость снижается, а скорость движения системы увеличивается. Для этого случая скорость движения системы определяется при помощи следующей формулы:

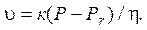(11.10)

На участке IV структура разрушена полностью (или образуются отдельные агрегаты частиц, ориентированные в потоке). Вязкость в этом состоянии становится постоянной, а ее значение — минимальным (η_min). Скорость движения системы с разрушенной структурой увеличивается пропорционально внешнему воздействию Р. Напряжение, характеризующее потерю прочности и полное разрушение структуры, обычно обозначают через Р_m.

Напряжение Р_к2можно определить, если продолжить прямую участка IV (см. рис. 11.5, а) до пересечения с осью абсцисс. Величину Р_к2называют условным (бингамовским) пределом, прочности.

Следует подчеркнуть, что на рис. 11.5 приведены реологические кривые течения твердообразных тел, когда соблюдается условие (11.3). Скорость перемещения жидкообразных тел в зависимости от внешнего воздействия показана на рис. 11.5, а [пунктирная кривая 1, проходящая через начало координат в соответствии с условием (11.2)].

При отсутствии структуры скорость была бы пропорциональна внешнему давлению, что соответствует линейной зависимости между v и Р (пунктирная прямая 1 2 на рис. 11.5, а). Такая зависимость характерна для ламинарного течения ньютоновской жидкости.

Вязкость структурированных систем определяется скоростью движения этих систем и тем внешним воздействием, которое заставляет систему течь. Вязкость является величиной переменной и изменяется от максимального η_maxдо минимального η_minзначения.

С увеличением внешнего воздействия происходит нарушение, а затем полное разрушение структурированной системы, что сопровождается уменьшением вязкости. Минимальная вязкость достигается тогда, когда структура связнодисперсной системы полностью разрушается.

Вязкость свободнодисперсных систем (в отсутствие деформации самих частиц) является величиной постоянной и не зависит от скорости течения и внешнего воздействия. Структурированные связнодисперсные системы обладают аномальной вязкостью, которая определяется внешним воздействием. Если такого воздействия нет или оно незначительно (участок I на рис. 11.5, б), то структура сохраняется и течение отсутствует.

В отличии от истинных ньютоновских жидкостей, течение которых описывается уравнениями (11.4) и (11.5), а их вязкость является величиной постоянной, вязкость структурированных жидкообразных систем зависит от внешнего воздействия в интервале Р_m< Р < Р_r. Подобные структурированные системы называют неньютоновскими (бингамовскими) жидкостями.

Подсолнечное масло является жидкообразной структурированной системой. Изменение вязкости подсолнечного масла в зависимости от скорости деформации dg/dt [см. формулу (11.5)] характеризуется следующими данными:

Скорость деформации, с^–1 0,4 10,4 200,4 3255,0

Вязкость, Па∙с 35,6 1,78 0,11 0,03

Из приведенных данных следует, что вязкость подсолнечного масла может изменяться в 104раз.

Изменение вязкости широко используется на практике. Для перекачки связнодисперсных систем необходимо создать такую скорость, которая соответствовала бы минимальной вязкости. Это позволит осуществлять транспортировку продукта по трубопроводу с минимальными затратами внешнего усилия. При перевозке в емкости, наоборот, требуется, чтобы продукт был структурированным и имел максимальную вязкость.

Дата добавления: 2014-10-15