Расклинивающее давление и агрегативная устойчивость

Потенциальный барьер и потенциальные ямы определяют агрегативную ycтойчивость и возможность коагуляции в зависимости от кинетической энергии частиц дисперсной фазы, которая определяется величиной kT (k — константа Больцмана), и характеризует энергию взаимодействия частиц, т.е. энергетический аспект этого взаимодействия.

Следует рассмотреть три возможных случая. При высоком потенциальном барьере, превышающем kT, и незначительной второй потенциальной яме (<kT) частицы не в состоянии преодолеть потенциальный барьер; коагуляция отсутствует и соблюдается устойчивость дисперсных систем с жидкой дисперсионной средой. Поэтому потенциальный барьер называют и коагуляционным барьером.

Когда потенциальный барьер и второй минимум незначительны (т.е. kT → 0), частицы в состоянии преодолеть потенциальный барьер и попасть в первую потенциальную яму; что приводит к коагуляции частиц и нарушению агрегативной устойчивости.

При средних значениях второй потенциальной ямы и потенциального барьера частицы не могут подойти друг к другу, и наблюдается фиксированное положение частиц при определенном достаточно большом расстоянии между ними.

На основании представлений о расклинивающем давлении можно определить силу и энергию аутогезии между двумя частицами, а также энергию и силу адгезии частиц в жидкой среде. Согласно теории Дерягина-Брэдли сила и удельная энергия (работа) аутогезионного (адгезионного) взаимодействия выражаются формулами (10.25) и (10.30).

Величина π(h) характеризует изменение расклинивающего давления (см. рис. 10.5, б) в зависимости от расстояния между частицами h. При помощи соотношений (10.25) и (10.31) можно проследить влияние на адгезию и аутогезию свойств жидкой среды, определяющих электростатическое отталкивание, адсорбционных процессов, рН среды и др.

Работа W_ког, затрачиваемая на преодоление потенциального барьера и обусловливающая коагуляцию твердых недеформированных частиц, приближенно можно выразить следующим образом:

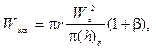(10.32)

где ; π(h)_би p(h)_п— расклинивающее давление, соответствующее

потенциальному барьеру и второй потенциальной яме (см. рис. 10.5, б).

Энергия (работа), которую следует затратить на преодоление аутогезионного взаимодействия между частицами (т.е. для отрыва частиц друг от друга) и осуществить процесс, обратный коагуляции, определяется по формуле

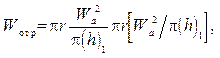(10.33)

где π(h)₁— расклинивающее давление, соответствующее первой потенциальной яме.

Следует обратить внимание на то, что, согласно формулам (10.32) и (10.33), работа формирования аутогезии частиц в процессе коагуляции и работа преодоления взаимодействия слипшихся частиц не равны между собой, что является следствием изменения расклинивающего давления в зависимости от расстояния между частицами.

Работа, определяемая при помощи формул (10.32) и (10.33), характерна для твердых, не подвергшихся деформации шарообразных частиц. В случае взаимодействия между двумя одинаковыми жидкими или газообразными частицами в эмульсиях и пенах (см. гл. 15 и 16), которые называют текучими в связи с подвижностью границы раздела, изменяется их профиль.

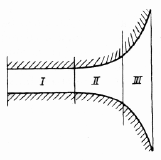Следует рассматривать три области: I — плоскопараллельную, II — переходную и III — объемного мениска (рис. 10.6). Межфазовое поверхностное натяжение в плоскопарал-лельной области является постоянным, а в области объемного мениска определяется условием (2.23) (см. гл. 2) и зависит от радиуса кривизны поверхности мениска. Кривизна поверхности в переходной области не является постоянной, что обусловливает переменное расклинивающее давление и межфазовое поверхностное натяжение.

С учетом особенностей взаимодействия текучих частиц сила аутогезии между каплями и пузырьками будет определяться следующим уравнением:

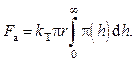(10.34)

Параметр kТможно определить в результате расчетов, он изменяется в пределах от 0,5 до 10.

Кроме того, под действием внешней силы Рпможет происходить деформация текучих частиц, в результате чего изменяется работа при контакте, последующей коагуляции и отрыве таких частиц. Соотношение между Wотри Wкогимеет вид

W_отр= W_ког(1 + α₁+ α₂), (10.35)

где α₁= π(h)_б/P_п; α₂= π(h)_п/Р_n.

Проведенный анализ позволяет выразить условия агрегативной устойчивости эмульсий в случае необратимой коагуляции при W_ког>> kT:

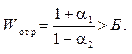(10.36)

Условие, определяющее самопроизвольное диспергирование осадка эмульсий, выглядит так:

Wотр= 1 + α₁+ α₂< Б, (10.37)

где Б — константа.

Влияние межфазового поверхностного натяжения на агрегативную устойчивость эмульсий и их способность к самопроизвольному диспергированию зависит от наличия потенциального барьера на изотерме поверхностного натяжения. При отсутствии потенциального барьера, когда π(h)б= 0 (см. рис. 10.5, б), по мере уменьшения межфазового поверхностного натяжения агрегативная устойчивость эмульсий снижается. Если потенциальный барьер будет значительным, то с уменьшением межфазового поверхностного натяжения наблюдается противоположный эффект, т.е. агрегативная устойчивость эмульсий растет.

Теория ДЛФО и учение о расклинивающем давлении постоянно совершенствуются и развиваются. Межмолекулярное взаимодействие и электростатическое отталкивание являются составляющими расклинивающего давления. Помимо них различают еще адсорбционную и структурную составляющие.

Адсорбционная составляющая расклинивающего давления связана с перераспределением молекул растворителя вблизи поверхности раздела фаз. В результате адсорбции концентрация веществ в тонкой пленке отличается от их концентрации в объеме жидкости. Перекрытие адсорбционных слоев под действием возникающих поверхностных сил (см. рис. 10.4) связано с изменением концентрации раствора и приводит к появлению дополнительной силы (отталкивания или притяжения) между двумя поверхностями, ограничивающими прослойку жидкости. Эта дополнительная сила и составляет адсорбционную компоненту расклинивающего давления π_а(h).

В граничных жидких слоях образуются структуры, которые отличаются от структуры этой же жидкости в объеме. Структуры, например, могут возникнуть в связи с сольватацией (в случае воды — гидратацией) поверхности частиц 1 (рис. 10.7) и образованием сольватной (гидратной) оболочки 2. При сближении частиц сольватные слои перекрываются, изменяются структура жидкости и свободная энергия системы [см. формулу (10.24)]. Возникает дополнительная сила отталкивания (или притяжения), вызванная структурной составляющей расклинивающего давления.

Кроме того, возможно отталкивание (позиция 7 на рис. 10.7) одноименно заряженных групп молекул (например, молекул воды), образующих сольватную (гидратную) оболочку. Отталкивание может оказать влияние на структурную составляющую расклинивающего давления.

Таким образом, в результате дальнейшего развития теории ДЛФО были определены четыре различные составляющие расклинивающего давления, а именно молекулярная π_м(h), электростатическая π_э(h), адсорбционная π_а(h) и структурная π_с(h):

π(h) = π_э(h) + π_м(h) + π_a(h) + π_c(h). (10.38)

Сочетание этих составляющих, которые проявляются в различных условиях, зависит от свойств дисперсной фазы и дисперсионной среды и определяет более сложный, чем приведенный на рис. 10.5, б, характер зависимости взаимодействия частиц на различных расстояниях, их разделяющих.

Дата добавления: 2014-10-15