
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Передаточная функция
|
|
|
|
Решение дифференциального уравнения (2.2) можно получить не только классическим методом, но также с использованием операционного исчисления, в основе которого лежит преобразование (интеграл) Лапласа.
Преобразование Лапласа представляет собой преобразование некоторой функции 
 вещественной переменной
вещественной переменной  в другую функцию
в другую функцию 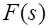 комплексной переменной
комплексной переменной 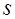 ,осуществляемое путем интегрирования
,осуществляемое путем интегрирования
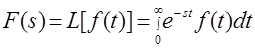 ,
,
где исходная функция называется оригиналом, а результат преобразования
называется оригиналом, а результат преобразования 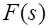 – изображением,
– изображением, 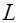 – оператор Лапласа.
– оператор Лапласа.
Существует соответствие между операциями с оригиналами и с изображениями. Так,  -кратному дифференцированию оригинала соответствует умножение изображения
-кратному дифференцированию оригинала соответствует умножение изображения 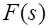 на
на  , а
, а  -кратному интегрированию оригинала в пределах от 0 до
-кратному интегрированию оригинала в пределах от 0 до  соответствует деление изображения
соответствует деление изображения 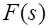 на
на  .
.
Функция-оригинал обладает следующими свойствами:
·  определена и кусочно-дифференцируема на всей положительной числовой оси;
определена и кусочно-дифференцируема на всей положительной числовой оси;
· 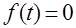 при
при 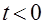 ;
;
- существует такое положительное число
 , при котором
, при котором  .
.
Для определения функции-оригинала по известному изображению применяют формулу обратного преобразования Лапласа

Максимальная величина  , при которой выполняется это неравенство, называется абсциссой абсолютной сходимости. В АСУ мы обычно имеем дело с функциями, для которых перечисленные выше условия выполняются.
, при которой выполняется это неравенство, называется абсциссой абсолютной сходимости. В АСУ мы обычно имеем дело с функциями, для которых перечисленные выше условия выполняются.
Выражения изображений Лапласа для некоторых элементарных функций приведены в табл.2.1. Более полные таблицы даны в справочной литературе.
Таблица 2.1
Изображения некоторых элементарных функций

| 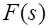
|
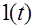
| 
|

| 
|
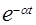
| 
|

| 
|

| 
|
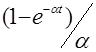
| 
|

| 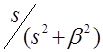
|
Передаточной функцией (в форме изображений Лапласа) называют отношение изображения выходной величины к изображению входной величины при нулевых начальных условиях
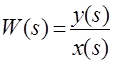 . (2.5)
. (2.5)
Введём для операции дифференцирования обозначение 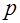 , т.е.
, т.е. 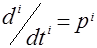 .
.
В операторной форме уравнение (2.2) имеет вид
 (2.6)
(2.6)
где 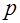 – оператор дифференцирования.
– оператор дифференцирования.
Передаточной функцией системы в операторной форме называют отношение
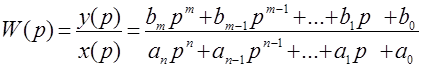 (2.7)
(2.7)
Передаточная функция определяет динамические характеристики системы или отдельных её элементов.
Итак, передаточная функция в форме изображений по Лапласу
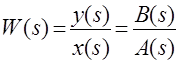 ,
,
 |
где
 ,
, 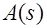 – полиномы числителя и знаменателя, характеризует систему в области изображений по Лапласу (рис. 2.12).
– полиномы числителя и знаменателя, характеризует систему в области изображений по Лапласу (рис. 2.12).
Рис.2.12. Модель системы (звена) в области изображений по Лапласу
Для линейных систем при нулевых начальных условиях нет необходимости переходить в область изображений, а систему (звено) можно представить блоком
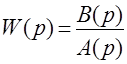 ,
,
как показано на рис. 2.13, и считать, что этот блок осуществляет те же действия, что предусматриваются дифференциальным уравнением (2.6), записанным в операторной форме
 ,
,
т. е.  – операторное звено во временной области.
– операторное звено во временной области.

Рис.2.13. Модель системы (звена) в операторной форме
Отметим, что (2.7) можно представить в виде отношения полиномов со свободными членами, равными единице
 ,
,
где  – коэффициент передачи;
– коэффициент передачи;
 ;
;
 .
.
Свободные члены могут равняться и нулю, если, например, в системе имеется интегрирующее звено.
Итак, для стационарных линейных звеньев (систем) при нулевых начальных условиях формально можно сделать подстановку 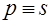 , так как в этом случае дифференцированию оригинала – символическому умножению оригинала на
, так как в этом случае дифференцированию оригинала – символическому умножению оригинала на 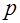 – соответствует умножение изображения на комплексное число
– соответствует умножение изображения на комплексное число 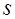 .
.
Все свойства преобразования Лапласа применимы для операторной формы записи дифференциальных уравнений линейных стационарных систем при нулевых начальных условиях, т.е. можно для таких систем считать  и тогда выражения (2.5) и (2.7) эквивалентны.
и тогда выражения (2.5) и (2.7) эквивалентны.
В знаменателе передаточной функции (2.7) записано выражение, аналогичное левой части характеристического уравнения. Поэтому можно считать, что знаменатель передаточной функции есть характеристический полином дифференциального уравнения

Корни характеристического уравнения 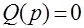 , будучи подставленными в (2.7), обращают передаточную функцию в бесконечность и называются полюсами передаточной функции. Корни уравнения
, будучи подставленными в (2.7), обращают передаточную функцию в бесконечность и называются полюсами передаточной функции. Корни уравнения 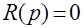 при подстановке в (2.7) обратят передаточную функцию в нуль и называются нулями передаточной функции.
при подстановке в (2.7) обратят передаточную функцию в нуль и называются нулями передаточной функции.
|
|
|
|
|
Дата добавления: 2014-10-15; Просмотров: 1842; Нарушение авторских прав?; Мы поможем в написании вашей работы!