Апериодическое звено первого порядка

Типовые динамические звенья

Любую систему можно представить в виде соединения звеньев – условно выделенных преобразователей сигнала направленного действия. Зная математические модели отдельных звеньев, можно получить модель всей системы.

Направленность действия означает, что сигнал передаётся от входа звена к выходу, а подключение других звеньев не оказывает влияния на свойства звена. Другими словами, включение звена в систему не изменяет его математической модели.

Типовые звенья описываются уравнениями не выше второго порядка, имеют один вход и один выход и являются элементами направленного действия.

Звено не обязательно соответствует функциональному элементу АСУ. Сложный элемент можно представить в виде соединения простых звеньев (не выше 2-го порядка), а соединение простых элементов – объединить в одно звено. Например, несколько последовательно соединённых усилителей заменяют одним с коэффициентом передачи, равным произведению коэффициентов усиления всех усилителей, входящих в соединение.

Рассмотрим вначале наиболее часто встречающиеся типовые звенья, а затем обратимся к особенностям их соединения и правилам преобразования структурных схем.

Дифференциальное уравнение такого звена имеет вид:

где 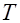– постоянная времени, с; 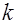– коэффициент усиления (передачи).

Передаточная функция

, (2.15)

а переходная функция при

.

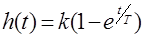При

.

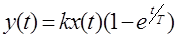2.5.2. Звенья второго порядка

Дифференциальные уравнения таких звеньев имеют вид

,

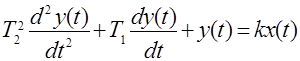а передаточная функция

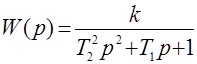(2.16)

В зависимости от соотношения постоянных времени , и 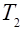звенья второго порядка подразделяются на апериодическое второго порядка и колебательные. В свою очередь колебательные звенья подразделяют на устойчиво колебательное (обычно его называют просто колебательным), консервативное и неустойчивое колебательное.

Соотношение , и 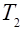выражают через коэффициент демпфирования . Обозначив 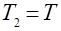, получим 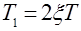и тогда (2.16) запишется в виде

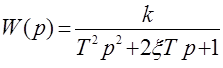(2.17)

Переходные процессы в звеньях второго порядка определяются видом корней характеристического уравнения.

Дата добавления: 2014-10-15