Уравнения

Связь устойчивости с корнями характеристического

Если

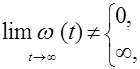(3.8)

то система будет нейтральной, и в соответствии с определением, неустойчивой.

Для решения дифференциального уравнения (3.2) требуется решить алгебраическое уравнение, называемое характеристическим:

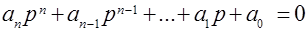(3.9)

Надо иметь ввиду, что здесь 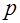уже не является оператором дифференцирования, а является комплексным числом и обозначение оставлено лишь для удобства.

Из теории линейных дифференциальных уравнений известно, что общее решение уравнения (3.2) есть

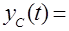
, (3.10)

где 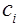– постоянная интегрирования; 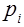– корни уравнения (3.9), которые ранее обозначались как .

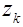Таким образом, переходной процесс 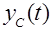представляет собой сумму составляющих, число которых определяется числом корней характеристического уравнения, т.е. порядком уравнения системы.

Уравнение 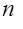–ой степени содержит 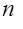корней. В общем случае

(3.11)

Корни 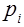могут быть вещественными, комплексными попарно–сопряжёнными, мнимыми попарно–сопряжёнными и нулевыми.

Если все корни разные, то их называют простыми. Если среди корней есть одинаковые, то их называют кратными. Принято по расположению на комплексной плоскости корни называть левыми, если 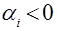и правыми, если .

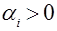Условие устойчивости формулируется так: для асимптотической устойчивости линейной системы необходимо и достаточно, чтобы все корни её характеристического уравнения были левыми.

Хотя корни p_i зависят только от вида левой части дифференциального уравнения линейной системы, постоянные интегрирования с_i зависят и от вида правой части. Поэтому форма переходного процесса и быстрота его затухания определяются как левой, так и правой частями. Однако в связи с тем, что устойчивость определяется только фактом наличия или отсутствия затухания переходного процесса, то устойчивость линейной АСУ определяется только видом характеристического уравнения.

Вещественными корням соответствуют слагаемые, представляющие собой экспоненты

.

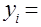
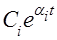Если 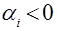, то получаем затухающие экспоненты (рис. 3.2,а).

При слагаемые представляют собой прямые, параллельные оси времени (рис. 3.2,б).

Положительным корням 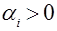соответствуют возрастающие экспоненты (рис. 3.2,в).

Комплексные корни всегда попарно–сопряжённые: 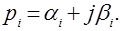и Слагаемые, определяемые этими корнями

.

Можно показать (с использованием известной формулы Эйлера), что указанная сумма равна

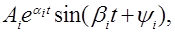
где – новые постоянные.

При 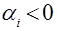в этом случае получаются затухающие колебания (рис. 3.2,д), а при 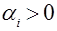– расходящиеся (рис. 3.2,е).

Рис. 3.2. Возможные расположения корней характеристического

уравнения на комплексной плоскости и соответствующие

составляющие переходного процесса

Дата добавления: 2014-10-15