Основные понятия устойчивости

Устойчивость линейных АСУ

Одним из основных условий работоспособности АСУ является её устойчивость, т.е. способность системы возвращаться в исходное состояние после снятия воздействия, выведшего её из этого состояния.

Рассмотрим понятие устойчивости, её связь с параметрами системы, а также некоторые критерии устойчивости.

Понятие устойчивости неразрывно связано с понятием равновесия. Равновесным состоянием тела (или системы) называется такое со стояние, в котором сумма всех внешних по отношению к телу (или системе) воздействий равна нулю.

Правильно спроектированная система должна устойчиво работать при всех внешних воздействиях.

Наглядно устойчивость равновесия показана на рис. 3.1, где изображён шар, расположенный в некотором углублении (рис. 3.1,а), на выпуклой поверхности (рис. 3.1,б) и на плоскости (рис. 3.1,в).

В точке А шар находится в положении равновесия.

В случае, изображённом на рис. 3.1,а, при всяком отклонении шара от положения равновесия под воздействием x, например, в точку В, он будет стремиться снова возвратиться к положению равновесия – точку А или во всяком случае в положение, близкое к точке А (при наличии сил трения). Такое положение равновесия устойчиво.

На рис. 3.1,б изображён случай неустойчивого положения равновесия. После снятия воздействия шар будет продолжать отклоняться и никогда не вернётся в начальное положение или близкое к нему.

Рис. 3.1. К понятию устойчивости

В случае, изображённом на рис. 3.1,в, после внешнего воздействия шар перейдёт в новое состояние равновесия (точка В), причём координата нового состояния равновесия зависит от величины воздействия. Рис. 3.1 иллюстрирует поведение устойчивой, неустойчивой и нейтральной системы.

В этом примере вопрос об устойчивости решается довольно просто. В общем случае не всегда просто найти условия, при которых равновесное положение АСУ будет устойчивым. Равновесное состояние нарушается при внешних воздействиях. Это могут быть сигнал управления, помехи и т.п.

Итак, в простейшем случае под устойчивостью АСУ подразумевается свойство системы возвращаться к первоначальному состоянию после прекращения воздействия, выведшего систему из этого состояния.

Такой тип устойчивости системы принято называть асимптотической устойчивостью. В дальнейшем в этой и последующих главах речь будет идти именно об этом типе устойчивости. Поэтому для краткости слово «асимптотическая» будем опускать.

Обозначим: у₀(t) – равновесное состояние системы, у(t) – состояние системы при наличии воздействия на нее x(t); тогда, согласно вышесказанному, АСУ будет являться устойчивой, если у(t) при t→∞ стремиться к своему начальному значению у₀(t) после снятия воздействия x(t).

Неустойчивая система не возвращается к состоянию равновесия по окончании воздействия, а непрерывно удаляется от него или совершает недопустимо большие колебания около него.

Следует различать устойчивость «в малом» и «в целом». Автоматические системы могут быть устойчивы при воздействиях, не выходящих за определенные пределы, и неустойчивы «в целом» при больших воздействиях.

Заметим также, что, согласно принятому нами определению, нейтральные АСУ, т.е. такие, в которых по окончании воздействия устанавливается новое состояние равновесия, отличное от первоначального и зависящее от произведенного воздействия, считаются неустойчивыми.

В данной главе при исследовании вопросов устойчивости будут рассматриваться только линейные АСУ, т.е. АСУ описываемые линейными дифференциальными уравнениями вида

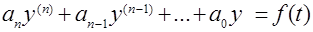, (3.1)

где – управляемая переменная, – выражение вида

зависящее от воздействия :

и – постоянные коэффициенты.

Предполагаем, что .

Функция , т.е. решение уравнения (3.1), зависит от величин коэффициентов и 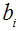, от входного воздействия и начальных значений и в момент времени =0, когда было приложено воздействие.

Если при 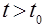, т.е. воздействие снято, то будет подчиняться уравнению свободного движения системы

(3.2)

Из теории линейных дифференциальных уравнений известно, что общее решение уравнения (3.1) есть

(3.3)

где 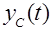– свободное движение системы, – вынужденное движение, и, следовательно, чтобы система могла правильно реагировать на сигнал управления , 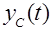должен стремиться к нулю с течением времени, т.е.

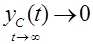(3.4)

Определение устойчивости, данное ранее, и требование (3.4) в данном случае эквивалентны.

Рассмотрим взаимосвязь устойчивости линейной АСУ с весовой функцией этой системы, т.е. будем считать, что кратковременное воздействие на систему, находящуюся в состоянии равновесия, производится единичным импульсом . В этом случае выходной сигнал и есть весовая функция

. (3.5)

Следовательно, если

(3.6)

система будет устойчивой.

Если же

(3.7)

то она неустойчива.

Дата добавления: 2014-10-15