Модель Леонтьева межотраслевого баланса

Постановка задачи. Пусть имеется n отраслей промышленности, каждая из которых производит продукцию, которая идет как для внутреннего потребления данной отраслью и другими отраслями, так и для конечного личного или общественного потребления. Обозначим х_i – общий (валовый) объем продукции i-отрасли, х_ij – объем продукции i-отрасли, потребляемой j-отраслью, y_i – объем конечного продукта i-отрасли. Имеем соотношение баланса:

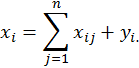
Введем коэффициенты прямых затрат 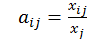. Если считать, что эти коэффициенты постоянны в течение некоторого периода времени, то x_ij = a_ij x_j, и соотношение баланса примет вид:

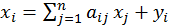или в матричном виде Х = А٠Х + У.

Задача состоит в нахождении такого вектора Х, который при известной матрице прямых затрат А обеспечивает конечный продукт У.

Решая полученное матричное уравнение, находим Х = (Е–А)^–1 У.

Матрица (Е – А)^–1 называется матрицей полных затрат.

Чтобы матричное уравнение было разрешимо, необходимо, чтобы матрица А была продуктивной. Есть несколько критериев продуктивности матрицы. Например, если максимум сумм элементов столбцов не более 1 и хоть одна сумма строго меньше 1, то матрица продуктивна.

Пример 1.9. Решение задачи поиска межотраслевого баланса [3, c. 99 – 104].

Имеется две отрасли производства, в таблице 1.9 указаны объёмы производства и потребления.

Таблица 1.9

Производство	Потребление	Конечный продукт	Валовый продукт
Энергетика	Маш.-ние
Энергетика
Машиностроение

Необходимо вычислить объем валового выпуска продукции каждой отрасли, если конечный продукт 1-й отрасли должен увеличиться в 2 раза, 2-й на 20 %.

Из таблицы 1.9 имеем:

х₁ = 500, х₂ = 400, у₁ = 240, у₂ = 85, х₁₁ = 100, х₂₁ = 275, х₁₂ =160, х₂₂ = 40.

Построим матрицу прямых затрат:

а₁₁ = 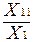= = 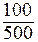0,2; а₁₂ = = = 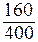0,4;

а₂₁ = 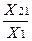= = 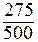0,55; а₂₂ = 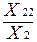= = 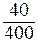0,1.

А = 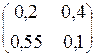, Е – А = – = .

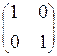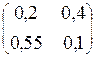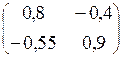Проверим матрицу А на продуктивность:

0,2 + 0,55 = 0,75 < 1, 0,4 + 0,1 = 0,5 < 1, т. е. матрица А продуктивна.

Найдем обратную к ней. Вычислим определитель:

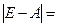0,8٠0,9 – 0,55٠ 0,4 = 0,5.

Тогда,

Вычислим по данным условия задачи новый вектор конечного продукта
У = (У₁, У₂):

У₁ = 240٠2 = 480, У₂ = 85 ٠(1+ 0,2) = 102. Имеем У_нов =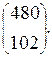

Тогда Х = = .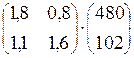

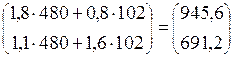1.15. В табице 1.10 приведены данные об исполнении баланса за отчетный период в усл. ден. ед.

Таблица 1.10

Отрасль	Потребление	Конечный продукт	Валовый продукт
Сфера обслуживания	Лёгкая пром-ть
Произ-водство	Сфера обс-ния
Лёгкая пром-ть

Вычислить необходимый объем валового выпуска каждой отрасли, если конечное потребление сферы обслуживания увеличится вдвое, а лёгкой промышленности сохранится на прежнем уровне.

1.16. Продуктивна ли матрица А:

1) 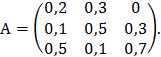2) .

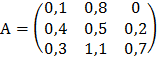1.17. Экономика разделена на три отрасли. В таблице 1.11 заданы коэффициенты прямых затрат и конечная продукция отраслей.

Таблица 1.11

Отрасль	Потребление	Конечный продукт
Сфера обслуживания	Лёгкая пром-ть	Сельское хоз.-во
Произ-водст-во	Сфера обс-ния	0,3	0,25	0,2
Лёгкая пром-ть	0,15	0,12	0,03
Сельское хоз.	0,1	0,05	0,08

Найти объем валовой продукции каждой отрасли, межотраслевые поставки, чистую продукцию отраслей.

1.18. Дана матрица полных затрат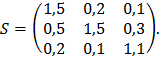

Найти приращение валового выпуска ∆Х, обеспечивающее приращение конечной продукции ∆У = (10, 30, 20).

1.19. Отрасль состоит из 4-х предприятий; вектор выпуска продукции и матрица внутреннего потребления имеют вид:

Х = 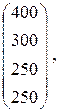А =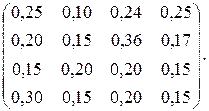

Пользуясь моделью Леонтьева, найти вектор объемов конечного продукта, предназначенного для реализации вне отрасли.

1.20. Данные баланса трех отраслей промышленности за некоторый промежуток времени даны в таблице 1.12. Требуется найти объем валового выпуска каждого вида продукции, если конечное потребление увеличить соответственно:

1) до 60, 70 и 30 единиц;

2) на 30, 10 и 50%.

Решить задачу методом обратной матрицы.

Таблица 1.12

№ п/п	Отрасль	Потребление отрасли	Конечный продукт	Валовый выпуск
	Добыча и переработка углеводородов
	Энергетика
	Машиностроение

Контрольные задания

Вариант 1.

1. Решить матричное уравнение:

.

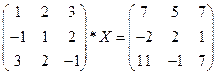2. Решить систему методом Крамера:

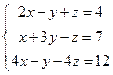
3. При каких значениях параметра к система не имеет решений, имеет бесконечно много:

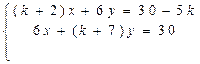
4. Решить методом Гаусса:

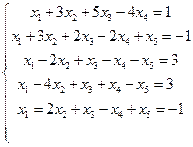
Вариант 2.

1. Продуктивна ли матрица:

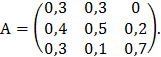
2. Решить систему матричным методом:

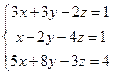
3. Решить методом Гаусса

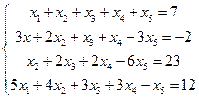
4. Решить задачу.

В первенстве России по футболу Спартак и Динамо вместе набрали на 11 очков больше, чем удвоенное число очков ЦСКА, утроенное число очков Динамо на 2 очка меньше, чем сумма удвоенного числа очков Спартака и ЦСКА. Известно, что число очков, набранных каждой командой, лежит в диапазоне от 15 до 25. Найти количество набранных каждой командой очков.

Вариант 3.

1. При каком значении m матрица не имеет обратной:

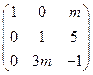
2. Решить систему матричным методом:

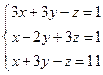
3. Решить методом Гаусса:

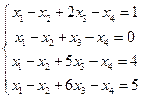
4. При каких значениях параметров а, в, с система имеет решение
x = 2, y = 1, z = 3

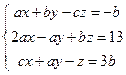
Дата добавления: 2014-10-15