
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Окружность. Эллипс. Гипербола. Парабола
1.50. Составить уравнение окружности с центром в заданной точке С и данным радиусом r: 1) С (4; –7), r = 5; 2) С (–6; 3), r = 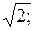 3) С (3; –2), r = 3.
3) С (3; –2), r = 3.
1.51. Окружность с центром в точке S (12; –5) проходит через начало координат. Составить уравнение этой окружности.
1.52. Составить уравнение окружности, диаметром которой является отрезок прямой 12 х + 5 у + 60 = 0, заключенный между осями координат.
1.53. Известно, что концы одного из диаметров окружности находятся в точках 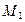 (2; –7) и
(2; –7) и 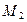 (–4; 3). Составить уравнение окружности.
(–4; 3). Составить уравнение окружности.
1.54. Составить уравнение прямой, проходящей через центры окружностей х 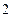 + у
+ у 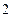 = 5 и х
= 5 и х 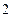 + у
+ у 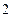 + 2 х + 4 у = 31. Найти отношение их радиусов..
+ 2 х + 4 у = 31. Найти отношение их радиусов..
1.55. Найти уравнение диаметра окружности х 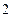 + у
+ у 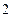 – 6 х + 14 у – 6 = 0, перпендикулярного хорде х – 2 у = 2.
– 6 х + 14 у – 6 = 0, перпендикулярного хорде х – 2 у = 2.
1.56. Найти полуоси, вершины, фокусы и эксцентриситет эллипса: 1) 9 х 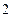 + 25 у
+ 25 у 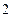 – 225 = 0; 2) 16 х
– 225 = 0; 2) 16 х 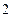 + 25 у
+ 25 у 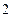 = 400.
= 400.
1.57. Найти координаты вершин, оси, фокусы, эксцентриситет и уравнения асимптот следующих гипербол:
1) 4 х  – 5 у
– 5 у 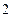 – 100 = 0; 2) 9 х
– 100 = 0; 2) 9 х 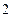 – 4 у
– 4 у 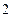 – 144 = 0;
– 144 = 0;
3) 16 х 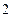 – 9 y
– 9 y 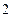 + 144 = 0; 4) 9 х
+ 144 = 0; 4) 9 х 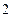 – 7 у
– 7 у 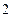 + 252 = 0.
+ 252 = 0.
1.58. Написать уравнение гиперболы, имеющей вершины в фокусах, а фокусы – в вершинах эллипса  +
+ 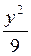 = 1.
= 1.
1.59. Составить уравнение параболы, проходящей через точки:
1) (0; 0) и (–1; –3) симметрично относительно оси ОХ;
3) (0; 0) и (2; –4) симметрично относительно оси ОУ.
1.60. Директрисой параболы, вершина которой находится в начале координат, является прямая 2 х – 3 = 0. Составить уравнение параболы и найти ее фокус.
1.61. Найти уравнение параболы и ее директрисы, если известно, что парабола симметрична относительно оси ОХ, точка пересечения прямых у = х и
х + у – 2 = 0 лежит на параболе и вершина параболы находится в точке с абсциссой, равной 0,5.
1.62. Найти расстояние от начала координат до прямой, проходящей через центр гиперболы у = 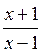 , и вершину параболы у = – 2 х
, и вершину параболы у = – 2 х 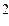 + 5 х – 2.
+ 5 х – 2.
1.63. Вершина параболы лежит в конце одного из диаметров окружности х 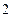 + у
+ у 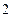 = 9. Составить уравнение параболы, если общая хорда параболы и окружности лежит на прямой у – 2 = 0.
= 9. Составить уравнение параболы, если общая хорда параболы и окружности лежит на прямой у – 2 = 0.
1.64. Составить уравнение прямой, проходящей через центр окружности х2 + у2 + 4х + 12у +15 = 0 параллельно прямой х + у = 0.
1.65. Составить уравнение параболы, симметричной относительно оси Ох, с вершиной в начале координат и проходящей через точку А(– 2; –3). Найти фокус и директрису параболы.
1.3.3. Прямая и плоскость в пространстве
Общее уравнение плоскости в пространстве: Ax + By + Cz + D = 0.
A (x–х0) + B (y–y0) + C (z–z0) = 0 – уравнение плоскости, проходящей через данную точку, где 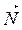 (А, В, С) – вектор, перпендикулярный плоскости – нормаль.
(А, В, С) – вектор, перпендикулярный плоскости – нормаль.
Каноническое уравнение прямой в пространстве:
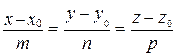 ,
,
где 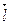 (m, n, p) – направляющий вектор прямой.
(m, n, p) – направляющий вектор прямой.
Взаимное расположение прямых и плоскостей определяется из условий параллельности и перпендикулярности нормали и направляющего вектора.
Пример 1.9. Составить уравнение плоскости, проходящей через точку
М (1; –2; 3) и перпендикулярной вектору  = (3; –4; 5).
= (3; –4; 5).
Решение.
Нормаль – это вектор, перпендикулярный плоскости (см. рис.1.4). В качестве 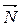 можно взять
можно взять 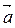 .
.
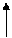




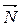
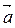
 |
Рис. 1.4. Перпендикулярность плоскости вектору
Тогда уравнение плоскости, перпендикулярной вектору 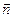 =(3; –4; 5) и проходящей через точку М (1; –2; 3) имеет вид:
=(3; –4; 5) и проходящей через точку М (1; –2; 3) имеет вид:
3(х – 1) – 4(y+2) + 5(z – 3) = 0 или 3х – 4y + 5z – 26 = 0.
Пример 1.10. Составить уравнение прямой, проходящей через точку
М0 (3; –2; 4), перпендикулярно плоскости 5х +3у –7z +1 = 0.
 Прямая перпендикулярна плоскости (рис. 1.5.), значит, в качестве её направляющего вектора можно взять нормаль плоскости, т.к. они коллинеарны.
Прямая перпендикулярна плоскости (рис. 1.5.), значит, в качестве её направляющего вектора можно взять нормаль плоскости, т.к. они коллинеарны. 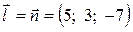 . И известна точка, через которую проходит прямая. Используем каноническое уравнение, получаем:
. И известна точка, через которую проходит прямая. Используем каноническое уравнение, получаем:


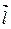
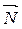



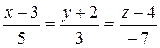 М
М 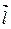 =
=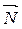
Рис. 1.5. Перпендикулярность прямой и плоскости
1.66. Составить уравнение плоскости, проходящей через точку 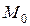 и перпендикулярной вектору
и перпендикулярной вектору 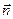 , если:
, если:
1) 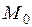 (2; –3; 1),
(2; –3; 1), 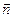 = (5; 1; –4); 2)
= (5; 1; –4); 2) 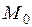 (1; 0; 1),
(1; 0; 1), 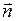 = (1; –2; 3).
= (1; –2; 3).
1.67. Составить уравнение плоскости, проходящей через ось ОУ и точку 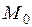 , если: 1)
, если: 1) 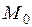 (2; –4; 3); 2)
(2; –4; 3); 2) 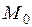 (–1; 2; –4).
(–1; 2; –4).
1.68. Составить уравнение плоскости, проходящей через точку М(1; –2; 3): а) перпендикулярной вектору 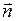 = (3; –4; 5); б) параллельной плоскости
= (3; –4; 5); б) параллельной плоскости
3х – 4у + 5z + 6 = 0; в) точку М1(0; 2; 5) и параллельной оси Оу; г) проходящей через ось Оz.
1.69. Найти проекцию В точки А(5; 2; –1): а) на плоскость 2х – у + 3z + 23 = 0; б) на прямую 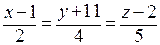 .
.
а) Решение.
Найдем уравнение прямой, проходящей через точку А (5; 2; –1) и перпендикулярной плоскости. В качестве направляющего вектора возьмем нормаль к плоскости 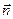 = (2; – 1; 3):
= (2; – 1; 3):
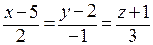 .
.
Запишем параметрическое уравнение прямой:
х = 5 + 2 t;
у = 2 – t;
z = –1 +3 t.
Найдем пересечение прямой и плоскости, для этого подставим полученные выражения в уравнение плоскости, получим:
2(5 + 2t) – (2 – t) + 3(–1 + 3t) + 23 = 0, откуда t = –2, т. е. точка пересечения имеет координаты хв = 1; ув = 4; zв = –7.
Ответ: В(1; 4; –7).
б) Для того, чтобы найти проекцию точки на прямую надо:
· построить плоскость, проходящую через заданную точку, перпендикулярно прямой,
· найти пересечение этой плоскости с прямой.
1.70. Составить уравнение плоскости, проходящей через точку М0 (2; –3;1) параллельно векторам  = (–3; 2; –1) и
= (–3; 2; –1) и  = (1; 2; 3)
= (1; 2; 3)
1.71. Составить уравнение плоскости, проходящей через точки М1(2; –15; 1) и М2 (–1; 1; –1) параллельно прямой, определяемой точками А (5; –2; 3) и В(6;1;0).
Контрольные задания
Вариант 1.
1. Составить уравнение прямой, проходящей через точку пересечения прямых 2х – 3у + 5=0 и 3х+ у –7 = 0, перпендикулярно прямой 5х + 4у + 8 = 0.
2. Определить вид кривой: 4x2 + 3y2 – 8x +12y – 32 = 0, построить ее.
3. Найти уравнение прямой, проходящей через точку (1;–2; 0) и перпендикулярной векторам (0; 3; –1) и (2; 1;–5)
4. Определить, при каких значениях к плоскость 2 к x – 3y + z + 3 = 0 будет параллельна прямой, проходящей через точки (2; –1, 1) и (3; –1; –3).
Вариант 2.
1. Составить уравнение перпендикуляра к прямой 8х + 4у –3 = 0 в точке ее пересечения с прямой х – у = 0.
2. Составить уравнение диаметра окружности x2 + y2 + 14y –6 x – 6 = 0, перпендикулярного хорде x – 2y = 2.
3. Найти уравнение плоскости, содержащей начало координат и перпендикулярной прямой, проходящей через точки (1; 1; –2) и (0; 7; –4).
4. Составить уравнение прямой, проходящей через точку (1; –3; 5), параллельно прямой 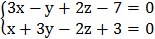 .
.
Вариант 3.
1. Дана прямая 2х + 5у – 1 = 0. Провести через точку М(–1; 3) прямую, параллельную данной и перпендикулярную данной.
2. Из точки М(–1;–1; 4) опущен на плоскость перпендикуляр, его основание Т(2; 1; 3). Составить уравнение плоскости.
3. Определить вид кривой, найти полуоси, фокусы, построить
5х2 + 9у2 – 30х + 18у + 9 = 0.
4. Определить взаимное расположение прямых в пространстве
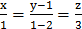 и
и 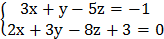 .
.
ГЛАВА 2. математический анализ
Основные разделы математического анализа: дифференциальное и интегральное исчисления функций одной и нескольких переменных, дифференциальные уравнения, числовые и степенные ряды широко используются при решении прикладных экономических задач. Все перечисленные разделы тесно взаимосвязаны и образуют стройную аксиоматическую теорию. Ряд заданий главы взят из пособия [4].
|
|
Дата добавления: 2014-10-15; Просмотров: 913; Нарушение авторских прав?; Мы поможем в написании вашей работы!