
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Скалярное, векторное, смешанное произведение векторов
|
|
|
|
Определение. Скалярным произведением двух векторов называется число, равное произведению длин векторов на косинус угла:
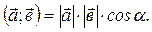
Вычисляется как сумма произведений соответствующих координат этих векторов (a,b) = x1x2 + y1y2 + z1z2.
Определение. Векторное произведение двух векторов – это вектор, перпендикулярный векторам a и b, образующий с ними правую тройку и имеющий длину
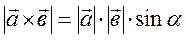
Вычисляется как определитель 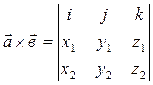 .
.
Геометрически длина векторного произведения равна площади параллелограмма, построенного на этих векторах.
О пределение. Смешанное произведение трех векторов это число, равное скалярному произведению третьего вектора на векторное произведение первых двух (a, b, c) = (a×b, c).
Вычисляется как определитель 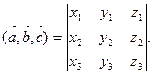
Геометрически модуль смешанного произведения векторов равен объёму параллелепипеда, построенного на этих векторах.
Если смешанное произведение равно нулю, то вектора лежат в одной плоскости, т. е. компланарны.
1.25. В табице 1.14 заданы векторы  ,
,  Вычислить:
Вычислить:
1) 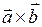 ; 2)
; 2) 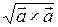 ; 3)
; 3) 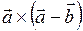 ; 4)
; 4) 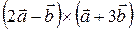 ;
;
5) угол между векторами  и
и  .
.
Таблица 1.14
| № | ||||
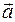
| (4, –2, –4) | (1, 4, –2) | (1, 1, 1) | (0, 1, 1) |

| (5, –1, 3) | (3, 1, 1) | (1, –1, 0,) | (–1, 1, 0) |
1.26. Найти и построить вектор  =
= 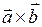 , если:
, если:
1)  = 2
= 2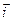 ,
,  = 3
= 3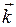 ; 2)
; 2)  =
= 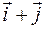 ,
,  =
= 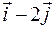 ;
;
3)  =
= 
 =
= 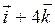 .
.
Определить в каждом случае площадь параллелограмма, построенного на векторах  и
и  .
.
1.27. Найти  ×
×  , синус угла между векторами
, синус угла между векторами  и
и  , если:
, если:
1)  = (1, –5, – 3),
= (1, –5, – 3),  = (–2, 4, 3);
= (–2, 4, 3);
2)  = (3, –2, 6),
= (3, –2, 6),  = (6, 3, –2);
= (6, 3, –2);
3) = (3, 0, –4),
= (3, 0, –4),  = (1, –2, 2).
= (1, –2, 2).
1.28. Найти площадь треугольника с вершинами:
1) А (2; 2; 2), В (1; 3; 3), С (3; 4; 2);
2) А (–3; –2; –4), В (–1; –4; –7), С (1; –2; 2).
1.29. Найти смешанное произведение  ,
,  и
и  , если:
, если:
1)  = (1, 1, 2),
= (1, 1, 2),  = (1, –2, 3),
= (1, –2, 3),  = (2, 1, 1);
= (2, 1, 1);
2)  = (5, –2, –1),
= (5, –2, –1),  = (1, –2, 1),
= (1, –2, 1),  = (1, 2, –2).
= (1, 2, –2).
1.30. Установить, компланарны ли векторы:
1)  = (1, 1, 3),
= (1, 1, 3),  = (0, 2, –1),
= (0, 2, –1),  = (1, –1, 4);
= (1, –1, 4);
2)  = (1, 2, 2),
= (1, 2, 2),  = (2, 5, 7),
= (2, 5, 7),  = (1, 1, –1).
= (1, 1, –1).
1.31. Вычислить объем параллелепипеда, построенного на векторах
 = (3, 2, 1),
= (3, 2, 1),  = (1, 0,–1),
= (1, 0,–1),  = (1, –2, 1).
= (1, –2, 1).
1.32. Треугольная пирамида задана координатами своих вершин
1) А (–1; 1; 0), В (2;–2; 1), С (3; 1; –1), Д (1; 0; –2).
2) А (–4; –4; –3), В (–2;–1; 1), С (2; –2; –1), D (1; 3; –2).
Найти: угол <ДАВ; S – площадь грани АВС, V – объём пирамиды, высоту пирамиды.
Решение.
1) Найдём векторы  и
и  :
:
 = (1 + 1; 0 – 1; – 2– 0) = (2; –1; –2),
= (1 + 1; 0 – 1; – 2– 0) = (2; –1; –2), 
 = (2 + 1; –2–1; 1 –0) = (3; –3; 1),
= (2 + 1; –2–1; 1 –0) = (3; –3; 1),
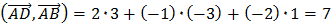 ,
,
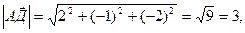
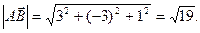

 .
.
2) Найдем вектор 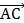 = (4; 0; –1), тогда векторное произведение
= (4; 0; –1), тогда векторное произведение
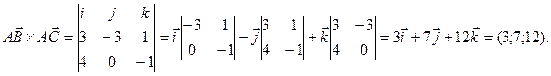
Его длина равна площади параллелограмма, построенного на этих векторах. Вычислим: 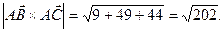 .
.
Тогда площадь ∆АВС равна половине площади параллелограмма:
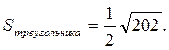
3) Найдём смешанное произведение:
 = 0 + 4+ 6 – (0+24+3)= –17.
= 0 + 4+ 6 – (0+24+3)= –17.
 ,
, 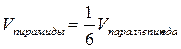 ,
,
Значит, 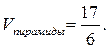
4) Т.к. 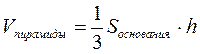 , то можно найти высоту пирамиды
, то можно найти высоту пирамиды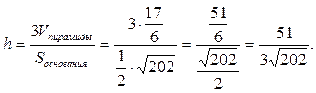
1.2.3. Линейные операторы.
Собственные векторы и собственные значения
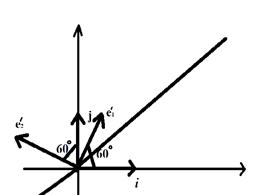
Любую квадратную матрицу можно рассматривать как линейный оператор, действующий на векторах. Матрица линейного оператора строится следующим образом: фиксируем базис линейного пространства (е1, е2) и действуем на базисные вектора данным преобразованием φ. Например, рассмотрим поворот на 60 (см.рис. 1.2); при этом базисные вектора переходят в вектора е1', e2'. Раскладываем эти образы по прежнему базису, коэффициенты разложения образуют столбцы матрицы линейного оператора преобразования.
(см.рис. 1.2); при этом базисные вектора переходят в вектора е1', e2'. Раскладываем эти образы по прежнему базису, коэффициенты разложения образуют столбцы матрицы линейного оператора преобразования.
 e1= i
e1= i 
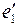 =
= 
e2 = j 
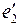 =
= 
A = 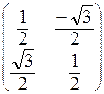 .
.
Рис. 1.2. Линейное преобразование поворота на 60˚
Определение. Вектор х называется собственным для матрицы А, если Ах = λх или (А – λЕ) х =0. Собственные числа λ являются корнями характеристического уравнения det (A – λE) = 0.
1.33. Линейный оператор 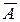 в базисе
в базисе 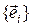 задан матрицей А. Найти образ
задан матрицей А. Найти образ где:
где:
1)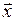 = 4
= 4 –3
–3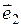 , А =
, А = ; 2)
; 2) 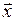 = 2
= 2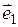 + 4
+ 4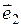 –
–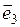 ,
,
А = 
1.34. Проверить непосредственным вычислением, какие из данных ниже векторов являются собственными векторами матрицы А, и указать соответствующие собственные значения:
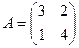 ,
, 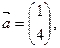
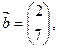


1.35. Найти собственные значения и собственные векторы линейных операторов, заданных матрицами:
1) А = 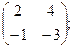 2) А =
2) А = 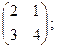
3) А =  4) А =
4) А = 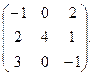
Задача о нахождении соотношения сбалансированности торговли
Постановка задачи. Пусть имеется несколько стран с известными национальными доходами Х = (х1, х2, …, хn). Структурная матрица торговли А показывает долю национального дохода, которую страна тратит на покупку товаров других стран и внутри своей страны. Требуется найти соотношение национальных доходов для сбалансированности торговли.
Математически эта задача сводится к отысканию собственного вектора матрицы А, отвечающего собственному значению 1.
Пример 1.8. Задана структурная матрица торговли 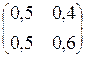 . Найти соотношение национальных доходов стран для сбалансированной торговли.
. Найти соотношение национальных доходов стран для сбалансированной торговли.
Решение:
 =
= 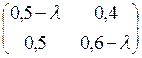 .
.
 =
= 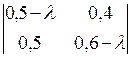 = (0,5 –
= (0,5 – 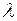 )٠(0,6 –
)٠(0,6 – 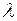 ) –2 = 0,3 – 0,5
) –2 = 0,3 – 0,5 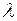 – 0,6
– 0,6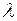 +
+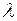 2 – 0,2 =
2 – 0,2 = 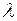 2 – 1,1
2 – 1,1 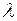 + 0,1 = 0.
+ 0,1 = 0.
Находим корни уравнения – собственные значения матрицы. Действительно, 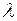 = 1,
= 1, 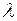 = 0,1. Тогда, собственный вектор для
= 0,1. Тогда, собственный вектор для 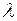 = 1:
= 1:
(А – 1Е) ٠ Х =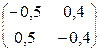 •
•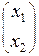 =
=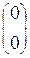 .
.
Имеем систему 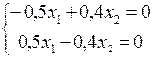 . Собственный вектор Х = (0,8; 1).
. Собственный вектор Х = (0,8; 1).
Соотношение доходов получается 0,8: 1 или 4: 5.
1.36. Структурная матрица торговли трех стран имеет вид:
А = 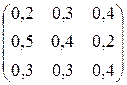 .
.
Найти бюджет первой и второй стран, удовлетворяющие сбалансированной бездефицитной торговле при условии, что бюджет третьей страны равен 1100 усл. ед.
1.37. Структурная матрица торговли четырех стран имеет вид:
A= .
.
Найти бюджеты этих стран, удовлетворяющие сбалансированной бездефицитной торговле, если сумма бюджетов 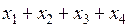 = 6270 усл. ед.
= 6270 усл. ед.
Контрольные задания
Вариант 1.
1. Найти разложение вектора a=(7;4;3) по базису e1=(1;2;0),
e2 =(3; –1; 2), e3 = (0; 4;–1).
2. Известно, что неколлинеарные векторы x(а;1) и у(в;1) являются собственными векторами матрицы 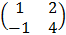 . Найти координаты а и в.
. Найти координаты а и в.
3. Определить длины векторов, на которых построен параллелограмм с диагоналями с = 2i – j + 3k и d = 2i –2j + 4k.
4. Найти площадь треугольника с вершинами: А (2; 1; 4), В (1; 0; 3), С (3; 1; 2).
Вариант 2.
1. Найти значение параметра а, при котором вектор (1,а) является собственным для матрицы 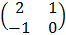 .
.
2. Найти длину вектора с = 2a – 3b,если |a| = 3, |b| = 2, угол между ними 60.
3. Образуют ли векторы базис e1 = (–2, 2, 4), e2 = (0, 1, 0), e3 = (2, –3, -4)?
4. При каком значении m вектора a = m i –3 j + 2 k и b = i + 2 j – m k перпендикулярны?
|
|
|
|
|
Дата добавления: 2014-10-15; Просмотров: 1810; Нарушение авторских прав?; Мы поможем в написании вашей работы!