
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Векторы. Линейные операции над векторами
|
|
|
|
Векторная алгебра
В этом параграфе рассматривается привычное понятие вектора, алгебраическая и геометрическая интерпретация операций над векторами, вводится обобщающее понятие векторного пространства как множества объектов разной природы, для которых заданы алгебраические операции сложения и умножения на число, удовлетворяющее определенным свойствам [3, c. 130].
В геометрии вектором называют направленный отрезок. Вектора можно складывать, вычитать, умножать на число. Если зафиксировать базис пространства, то произвольный вектор можно разложить по базису, коэффициенты этого разложения называются координатами вектора в этом базисе. Обычно рассматривают ортонормированный базис {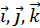 } векторы которого имеют единичную длину и перпендикулярны друг другу. Тогда, разложив вектор по базису
} векторы которого имеют единичную длину и перпендикулярны друг другу. Тогда, разложив вектор по базису
 =
=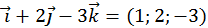 – координатная запись. Если вектора записаны в координатах, то операции сложения и умножения на число выполняются покоординатно, что согласуется с геометрическим определением суммы, разности и умножения на число.
– координатная запись. Если вектора записаны в координатах, то операции сложения и умножения на число выполняются покоординатно, что согласуется с геометрическим определением суммы, разности и умножения на число.
1.21. По данным векторам  ,
,  построить векторы:
построить векторы:
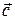 =
=  + 2
+ 2 ,
, 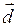 = 0,5
= 0,5 – 2
– 2 и найти их координаты:
и найти их координаты:
1)  = (1; 2),
= (1; 2),  = (2; –1); 2)
= (2; –1); 2)  = (–1; 1),
= (–1; 1),  = (3; 1);
= (3; 1);
3)  = (–2; –2),
= (–2; –2),  = (1; 1); 4)
= (1; 1); 4)  = (2; 4),
= (2; 4),  = (1; –1).
= (1; –1).
1.22. В треугольнике АВС проведена медиана АD. Выразить вектор  через векторы
через векторы 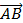 =
=  ,
,  =
= 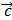 .
.
1.23. В некотором базисе даны векторы 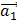 = (1; 2; 1),
= (1; 2; 1),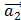 = (2; 1; 1),
= (2; 1; 1),
 = (–1; –2; –1). Найти все значения параметра m, при которых вектор
= (–1; –2; –1). Найти все значения параметра m, при которых вектор
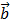 = (2; 3; m) линейно выражается через векторы
= (2; 3; m) линейно выражается через векторы  .
.
Задача о разложении вектора по базису
Имеются три вектора  = (–2; 0; 1),
= (–2; 0; 1),  = (1; –1; 0),
= (1; –1; 0), 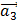 = (0; 1; 2). Выяснить, является ли вектор
= (0; 1; 2). Выяснить, является ли вектор  = (2; 3; 4) линейной комбинацией векторов
= (2; 3; 4) линейной комбинацией векторов  . Найти его разложение по базису.
. Найти его разложение по базису.
Решение.
Пусть = х
= х 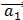 + у
+ у 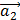 + z
+ z  . Необходимо найти коэффициенты разложения х, у, z.
. Необходимо найти коэффициенты разложения х, у, z.
Имеем, (2; 3; 4) = x(–2; 0; 1) + y(1; –1; 0) + z(0; 1; 2) или
(2; 3; 4) = (–2х + у; –у + z; х + 2z).
Приравняв координаты, получаем систему уравнений: 
Решаем её (х, у, z) = (–1,2; –0,4; 2,6), т. е вектор имеет разложение:
 = –1,2
= –1,2 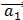 –0,4
–0,4 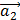 + 2,6
+ 2,6  .
.
1.24. Даны четыре вектора 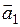 ,
,  ,
, 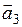 ,
, 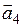 в таблице 1.12.
в таблице 1.12.
Таблица 1.12
| № | 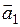
| 
| 
| 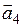
|
| (4, 5, 2) | (3, 0, 1) | (–1, 4, 2) | (5, 7, 8) | |
| (3, –5, 2) | (4, 5, 1) | (–3, 0, –4) | (–4, 5, –2) | |
| (–2, 3, 5) | (1, –3, 4) | (7, 8, –1) | (1, 9, 2) | |
| (1, 3, 5) | (0, 2, 0) | (5, 7, 9) | (0, 4, –2) |
Показать, что первые три из них образуют базис и найти координаты четвертого вектора в этом базисе.
|
|
|
|
|
Дата добавления: 2014-10-15; Просмотров: 430; Нарушение авторских прав?; Мы поможем в написании вашей работы!