Размещения

Определение. Размещениями из n элементов по k (n ³ k) называют множество комбинаций из k элементов, выбираемых из n элементов, отличающихся составом или порядком.

Число размещений из n элементов по k принято обозначать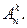

Пусть необходимо найти число размещений из n элементов по k. Существует n способов выбора первого элемента. После того как он выбран, остается (n − 1) способ выбора второго элемента. Для выбора третьего элемента остается (n − 2) способа, и вообще после выбора элементов от первого до (k − 1)-го остается (n – k + 1) способов для выбора k -го элемента. Таким образом, имеем

A_n^k = n × (n − 1) × (n − 2) ×…× (n – k + 1). (3.3)

Домножив и разделив правую часть формулы (3.3) на (n − k)!, получим:

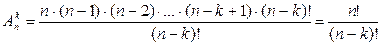(3.4)

Заметим, что понятие перестановок можно определить используя понятие размещений.

Определение. Размещения из n элементов по n называются перестановками.

Действительно, учитывая (3.3), имеем:

P_n = A_nⁿ = n × (n − 1) × (n − 2) ×…× (n – n + 1) = n!.

Используя формулу (3.4), получим тот же результат:

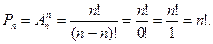
С помощью данного соотношения легко объяснить, почему принято считать 0!=1.

Пример 3.5. Сколько двухбуквенных комбинаций, не содержащих повторений, можно составить из 32 букв русского алфавита?

В данной задаче необходимо найти число размещений из 32 элементов по 2 по формуле (3.3):

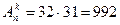двухбуквенных комбинаций.

По данным «Словаря русского языка», из этих 992 комбинаций только 114 являются словами. Например, да, ад, еж, яр и т. д.

Пример 3.6. Учащиеся 9 класса изучают 10 предметов. Сколькими способами можно составить расписание уроков на один день так, чтобы было 6 различных уроков?

По условию задачи расписание на один день должно быть составлено из 6 различных уроков, а всего 10 предметов. Поскольку важен порядок расположения уроков в расписании (какой урок первый, какой − второй и т. д.), следовательно, необходимо найти число размещений из 10 элементов по 6. Таким образом, в соответствии с формулой (3.4) получим:

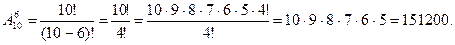
3.6. Сколько различных шестизначных телефонных номеров, не содержащих одинаковых цифр, можно составить из цифр: 1, 2, 3, 4, 5, 6, 7, 8 и 9?

3.7. В классе 25 учеников. Сколькими способами можно выбрать трех учащихся для участия в олимпиадах по математике, русскому языку и биологии?

3.8. В соревнованиях по бегу принимают участие 20 спортсменов. Сколькими способами могут быть распределены между участниками первое, второе и третье места?

3.9. Сколько различных трехбуквенных комбинаций можно составить из букв слова «гвоздика»?

Дата добавления: 2014-10-15