Правило произведения

Правило. Пусть множество А состоит из элементов (a₁, a₂,…a_m), множество В – из элементов (b₁, b₂,…b_k). Из множества А выбирается один из его m элементов и независимо от него из множества В выбирается любой из его k элементов. Множество всех пар, которые можно составить из элементов множеств А и В, можно записать в следующем виде:

(a_1, b₁), (a_1, b₂), …, (a_1, b_k),

(a_2, b₁), (a_2, b₂), …, (a_2, b_k),

………………………….

(a_n, b₁), (a_n, b₂), …, (a_n, b_k).

Таким образом, общее число N всех пар равно m × n:

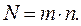
Следствие. С помощью метода математической индукции правило произведения распространяется на любое число конечных множеств и любое количество выбираемых из этих множеств элементов.

В формулировках задач на правило произведения часто используется союз русского языка «и» по аналогии с операциями пересечения множеств и конъюнкции.

Пример 3.9. В столовой предлагают два вида первых блюд, три вида вторых блюд и два вида десерта. Сколькими способами можно составить обед из трех блюд?

Обозначим множество первых блюд через А, вторых – В и третьих – С. Обозначив число способов, которыми можно составить обед из трех блюд через N и используя правило произведения, получим:

N = 2 × 3 × 2 = 12 способов.

Пример 3.10. В урне 3 красных и 4 синих шарика. Сколькими способами можно выбрать четыре шарика так, чтобы два из них были красными, а два – синими?

Обозначим множество красных шариков через А, синих– В. Обозначив число способов, которыми можно выбрать два красных шарика из множества А и два синих шарика – из множества В, через N и используя правило произведения, получим:

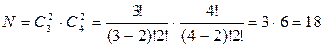способов.

Пример 3.11. В урне 5 красных, 7 белых и 4 зеленых шарика. Сколькими способами можно выбрать три шарика так, чтобы из них хотя бы два были красными?

Обозначим множество красных шариков через А, белых– В, зеленых – C. Вопрос, поставленный в задаче можно сформулировать следующим образом: сколькими способами можно выбрать три шарика так, чтобы было два красных шарика и один белый или два красных шарика и один зеленый или три красных шарика?

Обозначив число способов, которыми можно выбрать три шарика так, чтобы из них хотя бы два были красными через, N и, используя правила суммы и произведения, получим:

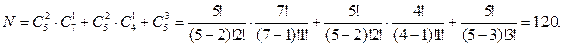
3.18. В вазе стоят пять розовых, семь красных и три белых розы. Сколькими способами можно выбрать три розы разного цвета? Сколькими способами можно выбрать три розы так, чтобы две были белые, а одна красная? Сколькими способами можно выбрать пять роз так, чтобы две из них были белыми, две красными и одна розовая?

3.19. В генетическом эксперименте использовали 4 белых, 7 красных и 5 розовых цветков гороха, которые были выбраны из имеющихся 10 белых, 10 красных и 10 розовых цветков. Сколькими способами можно было выбрать цветки для эксперимента?

3.20. В лабораторной клетке находятся 4 белых, 5 серых и 6 черных кроликов. Сколькими способами можно выбрать трех кроликов разного цвета? Сколькими способами можно выбрать шесть кроликов так, чтобы два из них были белыми, два серыми и два черными? Сколькими способами можно выбрать четырех кроликов так, чтобы два из них были белыми, один серый и один черный?

3.21. В урне 3 белых, 5 синих и 7 красных шариков. Сколькими способами можно выбрать три белых шарика и один синий? Сколькими способами можно выбрать пять шариков так, чтобы два из них были белыми, два – синими и один красным?

3.22. Из 10 красных и 7 белых гвоздик нужно составить букеты из трех цветов. Сколькими способами можно это сделать?

3.23. В 9 классе обучаются 11 мальчиков и 14 девочек. Сколькими способами можно выбрать 5 учащихся для участия в конкурсе КВН так, чтобы в команде было не менее трех мальчиков?

3.24. На книжной полке стоит собрание сочинений из 20 томов. Сколькими способами можно переставить книги так, чтобы первый и второй тома стояли рядом? Сколькими способами можно переставить книги так, чтобы третий и четвертый тома не стояли рядом?

Контрольные вопросы

1. Сформулировать определение понятия факториала. Как вычисляется факториал натурального числа?

2. Сформулировать определение понятия перестановок. Как вычисляются перестановки?

3. Сформулировать определение понятия размещений. Как вычисляются размещения?

4. Сформулировать определение понятия сочетаний. Как вычисляются сочетания?

5. Сформулировать правило сложения. Привести примеры применения правила сложения для решения задач комбинаторики.

6. Сформулировать правило произведения. Привести примеры применения правила произведения для решения задач комбинаторики.

Дата добавления: 2014-10-15