Решение вероятностных задач

Классический подход к понятию вероятности

В классическом походе к определению понятия вероятности рассматриваются частные случаи, в которых можно определить вероятность события без проведения большой серии испытаний. Этот подход предложен французским математиком П. Лапласом (1749−1817 гг.) и применим он только для моделей случайных событий с равновозможными исходами. Например, при рассмотрении опытов с бросанием игральной кости или монеты подразумевается, что они идеально симметричны, изготовлены из однородного материала, никогда не станут на ребро и не укатятся из поля зрения наблюдателя.

Определение. Событие В называется благоприятствующим событию A, если его наступление в результате испытания всегда приводит к наступлению события A.

Пример 3.18. Рассмотрим опыт с бросанием игральной кости. Пусть событие B – выпадение двойки на верхней грани игральной кости, а событие A – выпадение четного числа. Реализация в результате испытания события B всякий раз влечет за собой наступление события A, следовательно, событие B является благоприятствующим событию A.

Пример 3.19. Рассмотрим опыт, связанный с бросанием игральной кости, имеющий конечное число равновозможных, образующих полную группу исходов. В данном опыте возможны следующие исходы: U₁ – выпадение на верхней грани единицы, U₂ – двойки, U₃ – тройки, …, U₆ – шестерки. Действительно, события U₁, U₂, …, U₆ – попарно несовместны, т. к. в результате каждого испытания обязательно произойдет одно и только одно из этих событий.

При выполнении условия идеальной симметричности игральной кости (никакая из граней не утяжелена, грани кубика одинаковые и пр.) события U₁, U₂, …, U₆ в длинной серии испытаний реализуются с одинаковой частотой, т. е. являются равновозможными (равновероятными).

События, обладающие перечисленными свойствами, называются элементарными.

Определение. Элементарными событиями называются попарно несовместные, равновозможные события, образующие полную группу.

Совокупность элементарных событий называется пространством элементарных событий и обозначается Ω.

Пример 3.20. Рассмотрим опыт с бросанием монеты. Какие исходы в рамках данного опыта можно считать элементарными?

Элементарными являются следующие исходы (события): U₁ – выпадение орла, U₂ – выпадение решки. Действительно, если монета симметрична, то эти исходы являются равновозможными, попарно несовместными и образуют полную группу.

Пример 3.21. Рассмотрим опыт с бросанием двух монет. Какие исходы в рамках данного опыта можно считать элементарными?

С одной стороны, можно считать элементарными события: U₁ – выпадение на первой монете орла, U₂ – выпадение на первой монете решки, U₃ – выпадение на второй монете орла, U₄ – выпадение на второй монете решки. Действительно, перечисленные события удовлетворяют определению понятия элементарных событий.

С другой стороны, можно считать элементарными следующие события: H₁ – выпадение орла и на первой и на второй монетах, H₂ – выпадение решки и на первой и на второй монетах, H₃ – выпадение на первой монете решки, а на второй монете – орла, H₄ – выпадение на первой монете орла, а на второй монете – решки. События H_{1 ,} H_{2 ,} H₃ и H₄ также удовлетворяют определению понятия элементарных событий.

Необходимо отметить, что события U₁, U₂, U₃, U₄ и H_{1 ,} H_{2 ,} H₃, H₄ связаны между собой следующим образом:

H₁ =U₁× U₃, H₂ =U₂ × U₄, H₃ =U₂ × U₃, H₄ =U₁ × U_4.

Вывод. Оптимальный выбор элементарных событий часто значительно упрощает решение задачи.

Определение. Вероятностью события A называется отношение числа исходов N(A), благоприятствующих событию A, к полному числу элементарных исходов N:

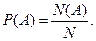(3.8)

Пример 3.22. Рассмотрим опыт с бросанием монеты. Найти вероятность выпадения орла.

Обозначим через A событие, связанное с выпадением орла. В рамках условия задачи всего два элементарных исхода: U₁ – выпадение орла, U₂ – выпадение решки. Из них благоприятным событию A является только одно. С помощью формулы (3.8) найдем вероятность события A:

Пример 3.23. Рассмотрим элементарные исходы, связанные с бросанием двух монет: H₁ – выпадение орла и на первой и на второй монетах, H₂ – выпадение решки и на первой и на второй монетах, H₃ – выпадение на первой монете решки, а на второй монете – орла, H₄ – выпадение на первой монете орла, а на второй монете – решки. Можно ли считать исходы H₃ и H_4, связанные с выпадением на одной монете орла, а на другой – решки, в одном испытании? Поставленный вопрос можно сформулировать иначе: сколько существует в рамках этой задачи элементарных исходов 3 или 4?

При классическом подходе к понятию вероятности, когда проводят лишь мысленный эксперимент, ответить на поставленный вопрос невозможно. Однако результаты реальных экспериментов, связанных с достаточно большими сериями испытаний, позволяют утверждать, что при проведении опыта с бросанием более чем одной монеты, более чем одного кубика и пр., монеты, кубикии т. д. различимы. Таким образом, исходы H₃ и H₄ являются различными исходами, следовательно, в рассматриваемой задаче 4 элементарных исхода.

Следовательно, вероятности событий H₁ – выпадения орла и на первой и на второй монетах и H₂ – выпадение решки и на первой и на второй монетах равны, т. к. только один исход является благоприятствующим этим событиям, а всего элементарных исходов – четыре, используя формулу (3.8), получим:

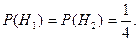
Вероятность события H, связанного с выпадением на одной монете орла, а на другой – решки, т. е. события H = H₃ + H₄, равна 1/2, т. к. два исхода являются благоприятными этому событию, а всего элементарных исхода – четыре, используя формулу (3.8), получим:

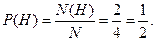
3.26. Рассмотрим опыт с бросанием двух монет. Найти вероятность выпадения:

а) хотя бы одного орла;

б) хотя бы одной решки;

в) не менее одной решки.

3.27. При проведении испытания с бросанием игральной кости найти вероятность выпадения на верхней грани кости:

а) шести очков;

б) пяти очков;

в) менее одного очка;

г) не более двух очков;

д) хотя бы трех очков;

ж) не менее пяти очков.

з) не менее двух и не более пяти очков.

Дата добавления: 2014-10-15