Перевірка статистичних гіпотез

Коефіцієнт варіації

Коефіцієнт варіації – (coefficient of variation) Показник мінливості щодо середньої величини.

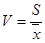
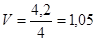
Коефіцієнт варіації дозволяє оцінити однорідність виміряного явища. Якщо коефіцієнт варіації ˃0,1 (V 0,1),то виміряне явище визначають неоднорідним. В іншому випадку – однорідним (V 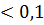). Критеріальним значенням квадратичного коефіцієнта варіації V служить 0,333 або 33,3%, тобто якщо V менший або дорівнює 0,333 – варіація вважається слабкою, а якщо більше 0,333 – сильною. У разі сильної варіації досліджувана статистична сукупність вважається неоднорідною, а середня величина – нетиповою і її не можна використовувати як узагальнюючий показник цієї сукупності.

Статистичні гіпотези поділяються на нульові й альтернативні.

Нульова гіпотеза є припущенням, про відсутність відмінностей у значеннях ознак, які зіставляють. Її позначають як Н_0.

Альтернативна гіпотеза – це припущення про існування відмінностей. Її позначають як Н_1.

Співвідношення емпіричного і критичного значень критерію є підставою для підтвердження чи спростування гіпотези. Статистичні критерії поділяються на параметричні й непараметричні. До формули розрахунку параметричних критеріїв належать показники розподілу, наприклад середні, дисперсії. Це класичні критерії, як z – критерій, t – критерій Стьюдента, F – критерій Фішера.

t-критерій Стьюдента. Це один з найбільш відомих параметричних критеріїв, який застосовується для визначення того, чи відносяться дві вибірки до однієї генеральної сукупності чи ні, або, по-іншому, для встановлення того, наскільки сильно відрізняються середні і дисперсії двох розподілів:

Особливості його наступні:

· Може бути використаний для встановлення відмінностей між двома вибірками в рівні досліджуваної ознаки, оскільки в його формулу обов'язково входить різниця середніх арифметичних двох вибірок;

· Чим більше різниця між середніми арифметичними двох вибірок, тим більше буде емпіричне значення t- критерия і тим більше вірогідне виявлення відмінностей;

· Критерій дозволяє сформулювати направлені гіпотези;

· Змінні повинні бути зміряні в шкалах інтервалів або відносин і, принаймні, теоретично, схильні до нормального розподілу;

· Вибірки можуть бути скільки завгодно великими.

	X	Y
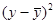
Середні
Суми

Порівнюємо отримані в експерименті значення t з табличним значенням з урахуванням ступенів свободи, рівних за формулою .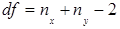

Ступені свободи – це кількість можливих напрямків мінливості деякої змінної. Загальноприйнятим позначенням числа ступенів свободи є df (від англ.. – degrees of freedom). У таблицях критичних значень наводяться або показники об’єму вибірки, або показники ступенів свободи. Cтупінь свободи (позначається як df або ν) – це величина, залежна від об’єму вибірки. Якщо ми не визначили ступінь свободи, то ми не зможемо користуватися статистичними таблицями. число ступенів свободи – це число даних з вибірки, значення яких можуть бути випадковими.

Якщо у нас є дві незалежні вибірки, то число ступенів свободи для першої з них складає n₁ – 1, а для другої – n₂ –1. Таким чином, число ступенів свободи для цих незалежних вибірок становитиме (n₁ + n₂) – 2.

У разі залежних вибірок число ступенів свободи дорівнює n –1.

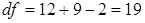t_0.05 = 2.09, t_0.01 = 2.86

Якщо t _емп ≥ t _кр, то робиться висновок про те, що отримані результати є статистично значимими (не випадковими) лише такі результати підтверджують експериментальну або альтернативну гіпотези.

Якщо t _емп ≤ t _кр, то робиться висновок про статистичну незначимість експериментальних результатів. Такі результати не можуть підтвердити експериментальну або альтернативну гіпотези, вони вважаються отриманими випадково.

Висновок: розподіли X і Y статистично не відрізняються (або, по-іншому, вибірки відносяться до однієї генеральної сукупності), оскільки t_емп < t_0.05.

Коли ми маємо справу з двома нормальними розподілами, що відрізняються один від одного за середнім значенням і дисперсією, застосовується спрощена формула наближених розрахунків:

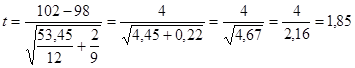
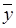Де і – середні арифметичні для результатів отриманих при першому і другому значеннях незалежної змінно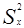ї.

і 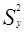– це дисперсі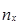ї.

і 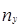– кількість результатів, отриманих при x та y відповідно значеннях незалежної змінної.

F-критерій Фішера. Параметричний критерій, що дозволяє оцінити відмінності в розподілі ознаки в двох вибірках, що мають однакові середні значення (тобто в тих випадках, коли t - критерій Стьюдента непридатний):

,

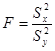при цьому в чисельнику завжди повинна бути більша дисперсія, а в знаменнику менша.

Як достоїнства, так і недоліки у нього ті ж, що і у t-критерия Стьюдента, але він виявляється непридатний для випадків, коли середні двох вибірок різні, оскільки отриманий висновок буде артефактом.

	X	Y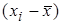
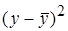
				-1
			-2	-4
			-3	-3
			-2
				-4
			-1	-1
Середні
Суми

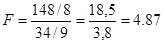F_0.05 = 3.23, F_0.01 = 5.47

df₁ – n-1=9-1=8

df₂ – n-1=10-1=9

Ступені свободи для більшої дисперсії розміщені по горизонталі, а для меншої ступені свободи розміщені по вертикалі.

Висновок: відмінності між двома розподілами статистично достовірні на 5% рівні значущості, оскільки F_емп > F_0.05, але недостовірні на 1% рівні, оскільки F_емп < F_0.01

Лекція 5-6

Дата добавления: 2014-10-15