Формулюються статистичні гіпотези

Порівняння емпіричних розподілів.

Під час проведення соціологічного опитування старшокласникам було запропоновано відповісти, якому з трьох можливих напрямків навчання (математичне, природно-наукове або гуманітарне) вони віддадуть перевагу надалі. Серед опитаних були і юнаки і дівчата. Дані зведені в таблицю крос-табуляції. Чи можна сказати, що перевага того чи іншого напряму навчання якось пов'язано з гендерним фактором?

Вихідні дані

	математика	Природничі науки	Гуманітарні науки
Юнаки
Дівчата

Взагалі візуальний аналіз таблиці дозволяє припустити, що юнаки більше бажають спеціальності, пов'язані з математикою, а дівчата - гуманітарні. Але як це довести за допомогою результатів статистичної обробки? Для цього треба порівняти чоловічий і жіночий розподіл переваг напрямків навчання.

До речі, не з усякими зведеними в таблицю даними можна здійснювати подібне порівняння. Вся справа в тому, що для застосування даного критерію є обмеження:

1) загальна сума частот по всім клітинкам повинна бути не менше 30 (n >30);

2) показники теоретичних частот (не емпіричних, а тільки теоретичних!) повинні бути не менше 5 (f_T >5). Рішення нашої задачі будується за наступним алгоритмом.

Н₀: розподіли переваг напрямів навчання в юнаків і у дівчат значно не відрізняються від випадкових.

Н₁: розподіли переваг напрямів навчання в юнаків і у дівчат значно відрізняються від випадкових.

2. У таблиці підраховуються суми частот по рядках і по стовпцях.

	Математика	Природничі науки	Гуманітарні науки	Сума частот по рядках
Юнаки
Дівчата
Сума частот по стовпцях				Загальна сума частот=65

3. Складається таблиця вирахування емпіричного значення χ.² У нульовому стовпці представлені дані по статі та вибору профілю навчання. У перший стовпець (f _е) заносяться значення емпіричних частот з попередньої таблиці. У другому стовпці (f_T) – похідні суми рядків на суму стовпців для відповідної клітинки, поділені на загальну суму частот (у нашому випадку–65). Це так звані теоретичні частоти, тобто значення, які могли вийти, якщо б не було значимих переваг у виборі (якщо б розподіли частот були незалежними). На цьому етапі ми відзначаємо, що таблиця відповідає вимогам щодо використання даного критерію (n > 30 і f_T >5). Третій стовпець містить результати обчислення виразів попереднього стовпця. Четвертий – різниця емпіричної та теоретичної частот. Потім отримані різниці зводяться в квадрат, діляться на теоретичні частоти і додаються.

	f е	fT	fT	f е – fT	(f е – fT)^2	(f е – fT)^2/ fT
Юнаки-математики		31·28/65	13,35	4,65	21,59	1,62
Юнаки-природничі науки		31·19/65	9,06	0,94	0,88	0,10
Юнаки-гуманітарні науки		31·18/65	8,58	-5,58	31,19	3,64
Дівчата-математики		34·28/65	14,65	-4,65	21,59	1,47
Дівчата-природничі науки		34·19/65	9,94	-0,94	0,88	0,09
Дівчата-гуманітарні науки		34·18/65	9,42	5,58	31,19	3,31
	10,23

Як і в попередньому випадку, емпіричний показник розраховується за формулою:

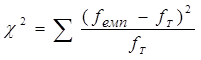
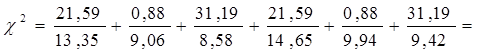
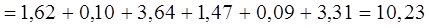
4. Визначаємо ступінь свободи. Для таблиці крос-табуляції з числом рядків, від двох і більше, формула виглядає дещо іншою ніж в попередніх випадках:

df= (k– 1)(c– 1)

df= (2 – 1)(3 – 1)=2

де k – кількість розрядів ознаки (рядків в таблиці емпіричних частот)

с – кількість розподілів для порівняння (стовпчиків в таблиці емпіричних частот)

За допомогою таблиці критичних значень порівнюємо отримане емпіричне значення з критичним (Табл. 4.6).

df	p=0,05	p=0,01
	5,991	9,210

Будуємо «вісь значимості»

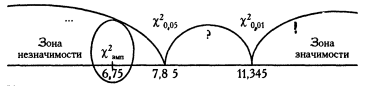
Емпіричне значення (χ²_емп =10,22) в необхідному рядку знаходиться правіше значення 9,210, відповідного р =0,01. Тобто р -рівень менше 0,01. Таким чином, емпіричне значення перевищує необхідне критичне для рівня р <0,01 (висока статистична значимість): χ²_емп ˃ χ²_кр. (р ≤0,01) приймаємо Н₁. Ми довели залежність переваги у виборі профілю подальшого навчання від статі респондента на рівні високої статистичної значущості. Таким чином, представники різних статей значно частіше бажають різні напрями навчання.

Дата добавления: 2014-10-15